| Теория | Практика |
Квадратичная функция
 Линейная функция
Линейная функция
 Обратная пропоциональность.
Обратная пропоциональность.
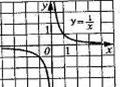 Функция у=
Функция у= 
 Полезно вспомнить:
Решение сложных задач целесообразно начать с повторения алгоритма решения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
При решении систем: Способ подстановки применим при решении систем, когда одно из уравнений является уравнением первой степени. Полезно помнить алгоритм решения этим способом:
1.Из уравнения первой степени выражают одну переменную через другую.
2.Подставляют полученное выражение в уравнение второй степени
3.Решают получившееся уравнение.
4. Находят соответствующие значения второй переменной.
Полезно вспомнить:
Решение сложных задач целесообразно начать с повторения алгоритма решения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
При решении систем: Способ подстановки применим при решении систем, когда одно из уравнений является уравнением первой степени. Полезно помнить алгоритм решения этим способом:
1.Из уравнения первой степени выражают одну переменную через другую.
2.Подставляют полученное выражение в уравнение второй степени
3.Решают получившееся уравнение.
4. Находят соответствующие значения второй переменной.
| 1. Прямая  касается окружности касается окружности  в точке с положительной абсциссой. Определите координаты точки касания.
Решение. 1) Найдем значения b, при которых система в точке с положительной абсциссой. Определите координаты точки касания.
Решение. 1) Найдем значения b, при которых система
 имеет единственное решение. Выполнив подстановку, получим уравнение имеет единственное решение. Выполнив подстановку, получим уравнение  , т.е. , т.е.  .
2) Плученное уравнение имеет единственное решение, когда его дискриминант равен нулю. Имеем: .
2) Плученное уравнение имеет единственное решение, когда его дискриминант равен нулю. Имеем: 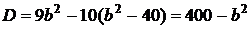 . Решив уравнение . Решив уравнение  , получим: , получим:  .
3) Таким образом, получили уравнения двух прямых, касающихся окружности: .
3) Таким образом, получили уравнения двух прямых, касающихся окружности:  и и  .
Найдем абсциссы точек касания, подставив найденные значения b в уравнение .
Найдем абсциссы точек касания, подставив найденные значения b в уравнение  :
при :
при  получим уравнение получим уравнение  , откуда , откуда 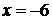 ; этот корень не удовлетворяет условию задачи;
при ; этот корень не удовлетворяет условию задачи;
при 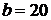 получим уравнение получим уравнение  , откуда , откуда  ; этот корень удовлетворяет условию задачи;
Найдем соответствующее значение y: ; этот корень удовлетворяет условию задачи;
Найдем соответствующее значение y:  .
Координаты точки касания: (6;2).
Ответ: (6;2).
2. Прямая .
Координаты точки касания: (6;2).
Ответ: (6;2).
2. Прямая  , где с — некоторое число, касается гиперболы , где с — некоторое число, касается гиперболы  в точке с отрицательными координатами. Найдите с.
Решение. Из уравнения в точке с отрицательными координатами. Найдите с.
Решение. Из уравнения  выразим y: выразим y:  . Графики функций . Графики функций  и и  имеют единственную общую точку в том и только том случае, если уравнение имеют единственную общую точку в том и только том случае, если уравнение  имеет один корень.
Получаем: имеет один корень.
Получаем:  ; ;  ; ; 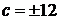 . Так как точка касания имеет отрицательные координаты, то . Так как точка касания имеет отрицательные координаты, то  (учащиеся могут прийти к этому выводу хотя бы из геометрических соображений). Поэтому, условию задачи удовлетворяет только (учащиеся могут прийти к этому выводу хотя бы из геометрических соображений). Поэтому, условию задачи удовлетворяет только  (в этом случае получаем прямую (в этом случае получаем прямую  , которая касается ветви гиперболы, расположенной в третьей четверти, т.е. в точке с отрицательными координатами).
Комментарий. Подробное обоснование, почему выбрано значение , которая касается ветви гиперболы, расположенной в третьей четверти, т.е. в точке с отрицательными координатами).
Комментарий. Подробное обоснование, почему выбрано значение  , не требуется. Возможно наличие схематичного рисунка.
Ответ: , не требуется. Возможно наличие схематичного рисунка.
Ответ:  .
3. Прямая .
3. Прямая  касается окружности касается окружности  в точке с положительной абсциссой. Определите координаты точки касания.
Решение. 1) Найдем значения b, при которых система в точке с положительной абсциссой. Определите координаты точки касания.
Решение. 1) Найдем значения b, при которых система
 имеет единственное решение. Выполнив подстановку, получим уравнение имеет единственное решение. Выполнив подстановку, получим уравнение  , т.е. , т.е.  .
2) Плученное уравнение имеет единственное решение, когда его дискриминант равен нулю. Имеем: .
2) Плученное уравнение имеет единственное решение, когда его дискриминант равен нулю. Имеем:  . Решив уравнение . Решив уравнение  , получим: , получим:  .
3) Таким образом, получили уравнения двух прямых, касающихся окружности: .
3) Таким образом, получили уравнения двух прямых, касающихся окружности:  и и  .
Найдем абсциссы точек касания, подставив найденные значения b в уравнение .
Найдем абсциссы точек касания, подставив найденные значения b в уравнение  :
при :
при  получим уравнение получим уравнение  , откуда , откуда  ; этот корень не удовлетворяет условию задачи;
при ; этот корень не удовлетворяет условию задачи;
при  получим уравнение получим уравнение  , откуда , откуда  ; этот корень удовлетворяет условию задачи;
Найдем соответствующее значение y: ; этот корень удовлетворяет условию задачи;
Найдем соответствующее значение y:  .
Координаты точки касания: (3;1).
Ответ: (3;1). Замечание. Выбрать касательную, удовлетворяющую условию задачи, можно и из графических соображений. Для этого достаточно схематически изобразить окружность и две прямые. .
Координаты точки касания: (3;1).
Ответ: (3;1). Замечание. Выбрать касательную, удовлетворяющую условию задачи, можно и из графических соображений. Для этого достаточно схематически изобразить окружность и две прямые.
|
| Модель 1 Баллы | Критерии оценки выполнения задания |
| 6 | Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
| 5 | Ход решения верный, все его шаги выполнены, но допущена вычислительная ошибка или описка. |
| 0 | Другие случаи, не соответствующие указанным критериям. |
| Модель 2 Баллы | Критерии оценки выполнения задания |
| 4 | Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
| 3 | Ход решения верный, все его шаги выполнены, но допущена вычислительная ошибка или описка. |
| 2 | Значение с выбрано неверно. |
| 1 | Указаны значения с = ±12. |
| 0 | Другие случаи, не соответствующие указанным критериям. |
Реши сам:
1. Найдите все значения k, при которых прямая  пересекает в трех различных точках график функции
пересекает в трех различных точках график функции
 .
.
2. При каких отрицательных значениях k прямая  пересекает параболу
пересекает параболу  в двух точках?
в двух точках?
3. При каких отрицательных значениях k прямая  и парабола
и парабола 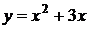 не пересекаются?
не пересекаются?
4. Постройте график функции: 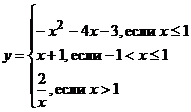
При каких значениях m прямая  имеет с графиком этой функции две общие точки?
имеет с графиком этой функции две общие точки?
5. Постройте график функции: 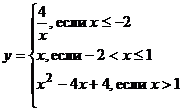
При каких значениях m прямая  имеет с графиком этой функции одну общую точку?
имеет с графиком этой функции одну общую точку?
6. При каких значениях а отрезок с концами в точках А (-5;-6) и В (-5; а) пересекает прямую  ?
?
7. При каких значениях а отрезок с концами в точках А (-3; a) и В (-3;-8) пересекает прямую  ?
?
Вернуться в содержание




