| Теория | Практика |
Решить систему уравнений – значит найти множество её решений.
Решением системы двух уравнений с двумя переменными является пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.
Системы уравнений с двумя переменными можно решать: а) графическим способом;
б) способом подстановки;
в) способом сложения (вычитания).
Выбор способа решения зависит от уравнений, входящих в систему.
Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.
Способ подстановки «хорош» при решении систем, когда одно из уравнений является уравнением первой степени. Полезно помнить алгоритм решения этим способом:
1.Из уравнения первой степени выражают одну переменную через другую.
2.Подставляют полученное выражение в уравнение второй степени
3.Решают получившееся уравнение.
4. Находят соответствующие значения второй переменной.
Способом сложения лучше пользоваться в случае, когда оба уравнения системы есть уравнения второй степени.


| 1. Решим систему уравнений
 Решение: Выразим из второго уравнения переменную x через y:
Решение: Выразим из второго уравнения переменную x через y:  .
Подставим в первое уравнение вместо x выражение .
Подставим в первое уравнение вместо x выражение  , получим уравнение с переменной y: , получим уравнение с переменной y:
 .
После упрощения получим равносильное уравнение .
После упрощения получим равносильное уравнение
 .
Решив его, найдем, что .
Решив его, найдем, что  , ,  . Подставив в формулу . Подставив в формулу   , получим: , получим:  .
Подставив в формулу .
Подставив в формулу  ; ;  , получим: , получим:
 .;Итак система имеет два решения: .;Итак система имеет два решения:
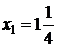 , ,  и и  , ,  . Ответ можно записать также в виде пар: . Ответ можно записать также в виде пар:  , ,  .
Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения.
2. Решим систему уравнений .
Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения.
2. Решим систему уравнений
 Решение: Т.К.
Решение: Т.К.  , выразим из второго уравнения переменную y через x: , выразим из второго уравнения переменную y через x:  .; Подставим в первое уравнение вместо y выражение .; Подставим в первое уравнение вместо y выражение  .
Получим уравнение относительно x: .
Получим уравнение относительно x:  . .  , , 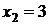 .
По формуле .
По формуле  находим y: находим y:
 , ,  .
Значит, система имеет два решения: .
Значит, система имеет два решения:
 , ,  и и  , ,  .
Ответ: .
Ответ:  , , 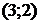 .
3. Вычислите координаты точки В.
Решение. Точка В является пересечением прямых .
3. Вычислите координаты точки В.
Решение. Точка В является пересечением прямых  и и  . Решив систему . Решив систему  , найдем, что , найдем, что  ; ;  .
Ответ: В (-3,4;0,4).
4. Решите систему уравнений .
Ответ: В (-3,4;0,4).
4. Решите систему уравнений  .
Решение. Преобразуем второе уравнение системы .
Решение. Преобразуем второе уравнение системы  к виду к виду  . Подставим в него . Подставим в него  . Выполнив преобразования, получим систему: . Выполнив преобразования, получим систему:
 .
Решив эту систему, получим: (-2;6), (3;-4).
Ответ: (-2;6), (3;-4). Возможна запись ответа в другом виде: .
Решив эту систему, получим: (-2;6), (3;-4).
Ответ: (-2;6), (3;-4). Возможна запись ответа в другом виде:  , ,  , , 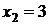 , ,  , или , или 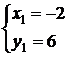 и и  .
Другое возможное решение. Выразим из первого уравнения одну из переменных через другую, например, .
Другое возможное решение. Выразим из первого уравнения одну из переменных через другую, например,  . Подставим . Подставим  во второе уравнение системы, получим уравнение во второе уравнение системы, получим уравнение 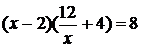 . После преобразований получим квадратное уравнение . После преобразований получим квадратное уравнение  .
Найдем корни данного уравнения и соответствующие значения y, получим: (-2;6), (3;-4). .
Найдем корни данного уравнения и соответствующие значения y, получим: (-2;6), (3;-4).
|
Реши сам:
1. (Демо 2010 задание 10) Окружность, изображенная на рисунке, задается уравнением  . Используя этот рисунок, для каждой системы уравнений укажите соответствующее ей утверждение.
. Используя этот рисунок, для каждой системы уравнений укажите соответствующее ей утверждение.
 А)
А)  1) Система имеет одно решение
1) Система имеет одно решение
Б)  2) Система имеет два решения
2) Система имеет два решения
В)  3) Система не имеет решений
3) Система не имеет решений
| А | Б | В |
Ответ:
2. Для каждой системы уравнения определите число ее решений (используйте графические соображения). В таблице под каждой буквой запишите номер соответствующего ответа.
А) 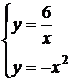 1) Нет решений
1) Нет решений
Б)  2) Одно решение
2) Одно решение
В)  3) Два решения
3) Два решения
| А | Б | В |
Ответ:
3. Вычислите координаты точки В. 
Ответ:______________
 4. На рисунке изображен график функции
4. На рисунке изображен график функции 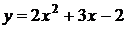 . Вычислите абсциссу точки А.
. Вычислите абсциссу точки А.
Ответ:_________
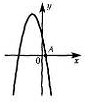 5. На рисунке изображен график функции
5. На рисунке изображен график функции  . Вычислите абсциссу точки А.
. Вычислите абсциссу точки А.
Ответ:_________
6. Решите систему уравнений: 
Ответ:_________
7 -10. Решите способом подстановки систему уравнений:
7. 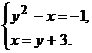 8.
8. 
9.  10.
10. 
11. Решите систему уравнений: 
1) (5;-3), (-5;3) 2) (-5;7), (3;-1)
3) (5;-3), (-3;5) 4) (-5;7), (5;-7)
12. Решите систему уравнений: 
1) (6;2), (-6;-2) 2) (-2;-6), (6;2)
3) (6;-2), (2;-6) 4) (-6;-10), (2;-2)
13. Для каждой системы уравнений определите число ее решений (используйте графические соображения).
В таблице под каждой буквой запишите номер соответствующего ответа.
А)  Б)
Б)  В)
В) 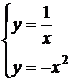
1) Два решения 2) Одно решение 3) Нет решений
Ответ:
| А | Б | В |

14. На рисунке изображен график функции у = 5х2 + 14х - 3. Вычислите абсциссу точки А.
Ответ:______________
15. Решите систему уравнений:  . Ответ:___________
. Ответ:___________
Вернуться в содержание
Тема 11 Составление уравнения по условию текстовой задачи
| Теория | Практика |
Решение сложных задач целесообразно начать с повторения алгоритма решения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
2. Задачи на движение по реке. При решении задач на движение по реке необходимо учесть, что
 , ,  где: где:
 – скорость по течению реки; – скорость по течению реки;
 – скорость объекта при движении против течения реки; – скорость объекта при движении против течения реки;
 – собственная скорость движущегося объекта; – собственная скорость движущегося объекта;
 – скорость течения реки. – скорость течения реки.
| 1. Расстояние между двумя причалами по реке 14 км. На путь против течения реки лодка затратила на 1 ч больше, чем на обратный путь по течению. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.
Обозначьте буквой х собственную скорость лодки (в км/ч) и составьте уравнение по условию задачи.
1)  2) 2)  3)
3)  4) 4)  Решение. x (км/ч) — собственная скорость лодки, тогда
Решение. x (км/ч) — собственная скорость лодки, тогда  (км/ч) — скорость по течению, (км/ч) — скорость по течению,  (км/ч) — скорость против течения.
Расстояние между причалами 14 км, следовательно, (км/ч) — скорость против течения.
Расстояние между причалами 14 км, следовательно,
 (ч) — время движения лодки по течению; (ч) — время движения лодки по течению;
 (ч) — время движения лодки против течения.
Время движения лодки против течения больше, чем по течению, на 1 час, поэтому составим уравнение: (ч) — время движения лодки против течения.
Время движения лодки против течения больше, чем по течению, на 1 час, поэтому составим уравнение:  .
Ответ: 2.
2. Прочитайте задачу: «От турбазы до станции турист доехал на велосипеде за 5 ч. На мопеде он мог бы проехать это расстояние за 3 ч. Известно, что на мопеде он едет со скоростью на 8 км/ч больше, чем на велосипеде. Чему равно расстояние от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено расстояние (в км) от турбазы до станции.
1) .
Ответ: 2.
2. Прочитайте задачу: «От турбазы до станции турист доехал на велосипеде за 5 ч. На мопеде он мог бы проехать это расстояние за 3 ч. Известно, что на мопеде он едет со скоростью на 8 км/ч больше, чем на велосипеде. Чему равно расстояние от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено расстояние (в км) от турбазы до станции.
1)  3) 3)  2)
2)  4) 4) 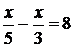 Решение. Пусть х км — расстояние от турбазы до станции. Тогда
Решение. Пусть х км — расстояние от турбазы до станции. Тогда  км/ч — скорость, с которой турист едет на велосипеде; км/ч — скорость, с которой турист едет на велосипеде; 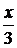 км/ч — скорость, с которой турист едет на мопеде. Известно, что скорость на мопеде на 8 км/ч больше скорости на велосипеде: запишем уравнение км/ч — скорость, с которой турист едет на мопеде. Известно, что скорость на мопеде на 8 км/ч больше скорости на велосипеде: запишем уравнение  .
Уравнение может быть записано и в другом виде, например, .
Уравнение может быть записано и в другом виде, например,  , но его легко преобразовать к виду: , но его легко преобразовать к виду:  .
Ответ: 3. .
Ответ: 3.
|
Реши сам:
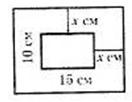
1. (Демо 2010 задание 11) Прочитайте задачу: «Фотография имеет форму прямоугольника со сторонами 10 см и 15 см. Ее наклеили на белую бумагу так, что вокруг всей фотографии получилась белая окантовка одной и той же ширины. Площадь, которую занимает фотография с окантовкой, равна 500 см2. Какова ширина окантовки?».
Пусть ширина окантовки равна х см. Какое уравнение соответствует условию задачи?
 1)
1) 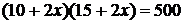
2) 
3) 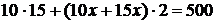
4) 
2. Прочитайте задачу.
Расстояние между двумя пристанями 24 км. Лодка проплыла от одной пристани до другой и вернулась обратно, затратив на весь путь 5 часов.
Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.Обозначьте буквой х собственную скорость лодки (в км/ч) и составьте уравнение по условию задачи.
1)  2)
2)  3)
3) 
3. Прочитайте задачу: «Периметр прямоугольника равен 20 см. Длины его смежных сторон относятся как 3: 2. Найдите длины сторон этого прямоугольника».
Пусть a и b – стороны прямоугольника, причем a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)  3)
3) 
2)  4)
4) 
4. Прочитайте задачу: «Периметр прямоугольника равен 10 см. Длины его смежных сторон относятся как 3: 2. Найдите длины сторон этого прямоугольника».
Пусть a и b – стороны прямоугольника, причем a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)  2)
2)  3)
3)  4)
4) 
5. Прочитайте задачу: «Периметр прямоугольника равен 30 см. Длины его смежных сторон относятся как 4: 1. Найдите длины сторон этого прямоугольника».
Пусть a и b – стороны прямоугольника, причем a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)  2)
2)  3)
3)  4)
4) 
6. Прочитайте задачу: «Периметр прямоугольника равен 10 см. Длины его смежных сторон относятся как 4: 1. Найдите длины сторон этого прямоугольника».
Пусть a и b – стороны прямоугольника, причем a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)  2)
2)  3)
3)  4)
4) 
7. Прочитайте задачу: «В трех группах детского сада 70 детей. В старшей группе в 3 раза меньше, чем в старшей, а в средней на 15 больше, чем в младшей. Сколько детей в старшей группе?»
Какое уравнение соответствует условию задачи, если буквой х обозначено число детей в старшей группе?
1)  2)
2) 
3)  4)
4) 
8. Прочитайте задачу: «Периметр прямоугольника равен 30 см. Длины его смежных сторон относятся как 2: 1. Найдите длины сторон этого прямоугольника».
Пусть a и b – стороны прямоугольника, причем a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)  2)
2)  3)
3)  4)
4) 
9. Прочитайте задачу: «В первый день школьник прочитал 29 страниц, во второй – 34 страницы, и вместе это составило 0,3 числа страниц в книге. Сколько страниц в книге?»
Какое уравнение соответствует условию задачи, если буквой х обозначено число страниц в книге?
1)  2)
2)  3)
3)  4)
4) 
10. В классе 25 учащихся. При посадке деревьев в школьном саду каждая девочка посадила по 2 дерева, а каждый мальчик – по 3 дерева. Всего было посажено 63 дерева, Сколько в классе девочек?
Пусть в классе х девочек. Какое уравнение соответствует условию задачи?
А.  Б.
Б.  В.
В.  Г.
Г. 
11. В спортивной секции занимается 26 детей. Каждая девочка имеет по 2 медали, а каждый мальчик – по 3 медали. Всего мальчики и девочки имеют 68 медалей. Сколько в секции занимается мальчиков?
Пусть в секции х мальчиков. Какое уравнение соответствует условию задачи?
А.  Б.
Б. 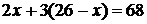
В.  Г.
Г. 
12. В кружке занимается 20 детей. К празднику каждая девочка сделала по 4 сувенира, а каждый мальчик – по 3 сувенира. Всего было сделано 72 сувенира. Сколько в кружке занималось девочек?
Пусть в кружке х девочек. Какое уравнение соответствует условию задачи?
А.  Б.
Б. 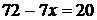
В.  Г.
Г. 
Вернуться в содержание






