| Теория | Практика |
Прогрессии
1. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.
Число d – разность прогрессии.  ; ;  Формула n -го члена:
Формула n -го члена:  Свойство прогрессии:
Свойство прогрессии:  Сумма n -членов:
Сумма n -членов:  или или 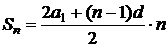 2. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и тоже число q, называется геометрической прогрессией.
Число q – знаменатель прогрессии.
2. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и тоже число q, называется геометрической прогрессией.
Число q – знаменатель прогрессии.  ; ;  Формула n -го члена:
Формула n -го члена:  Свойство прогрессии:
Свойство прогрессии:  Сумма n -членов:
Сумма n -членов:  , ,  Если
Если  , то прогрессия называется бесконечно убывающей геометрической прогрессией. , то прогрессия называется бесконечно убывающей геометрической прогрессией.
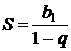
| 1. Последовательность ( ) - арифметическая прогрессия, в которой ) - арифметическая прогрессия, в которой  и и 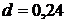 . Найдем пятидесятый член этой прогрессии.
Имеем: . Найдем пятидесятый член этой прогрессии.
Имеем:  .
2. Геометрическая прогрессия задана условиями: .
2. Геометрическая прогрессия задана условиями:  , ,  . Какое из данных чисел является членом данной прогрессии?
1) 6 2) 12 3) 24 4) 27
Решение: Выпишем несколько первых членов прогрессии: 3, 9, 27; число 27 является ее членом.
Ответ: 4.
Другой способ. Если заметить, что члены прогрессии — это степени числа 3, то можно сразу указать ответ, так как среди приведенных чисел, 27 является единственным числом, отвечающим этому условию.
3. Формулой n -го члена . Какое из данных чисел является членом данной прогрессии?
1) 6 2) 12 3) 24 4) 27
Решение: Выпишем несколько первых членов прогрессии: 3, 9, 27; число 27 является ее членом.
Ответ: 4.
Другой способ. Если заметить, что члены прогрессии — это степени числа 3, то можно сразу указать ответ, так как среди приведенных чисел, 27 является единственным числом, отвечающим этому условию.
3. Формулой n -го члена  задана последовательность, какое из следующих чисел не является ее членом:
А) задана последовательность, какое из следующих чисел не является ее членом:
А) 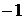 Б) Б)  В) В)  Г) Г)  .
Решение: можно непосредственно вычислять один за другим члены последовательности —
Получим .
Решение: можно непосредственно вычислять один за другим члены последовательности —
Получим  , , 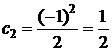 , ,  , , 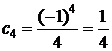 , ,  . первые три указанных числа являются членами последовательности, а это означает, что верный ответ дан под буквой Г. Можно «для убедительности» найти и . первые три указанных числа являются членами последовательности, а это означает, что верный ответ дан под буквой Г. Можно «для убедительности» найти и  , т.е. число , т.е. число  действительно не является членом последовательности. действительно не является членом последовательности.
|
Реши сам:
1. (Демо 2010 задание 12) Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие 
1)  2)
2) 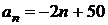 3)
3)  4)
4) 
2. Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее. 1)  2) 1,2,4,8 3)
2) 1,2,4,8 3)  4)
4) 
3. Геометрическая прогрессия задана условиями:  ,
,  . Какое из данных чисел является членом данной прогрессии? 1) 6 2) 12 3) 24 4) 27
. Какое из данных чисел является членом данной прогрессии? 1) 6 2) 12 3) 24 4) 27
4. Для каждой арифметической прогрессии, заданной формулой n -го члена, укажите ее разность d.
А)  Б)
Б)  В)
В) 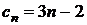
1)  2)
2)  3)
3)  4)
4) 
Ответ:
| А | Б | В |
5. Для каждой арифметической прогрессии, заданной формулой n -го члена, укажите ее разность d.
А)  Б)
Б)  В)
В) 
1)  2)
2)  3)
3)  4)
4) 
Ответ:
| А | Б | В |
6. Геометрическая прогрессия задана условиями:  ,
,  . Какое из данных чисел является членом данной прогрессии?
. Какое из данных чисел является членом данной прогрессии?
1) 10 2) 16 3) 18 4) 24
7. Геометрическая прогрессия задана условиями:  ,
,  . Какое из данных чисел является членом данной прогрессии?
. Какое из данных чисел является членом данной прогрессии?
1) 27 2) 22 3) 15 4) 12
8. Последовательности заданы несколькими первыми членами. Одна из них — геометрическая прогрессия. Укажите ее.
1)  3)
3) 
2)  4)
4) 
9. Какое из чисел является членом арифметической прогрессии, заданной формулой а n = 2n+1.
А. -10 Б. 0 В. 11 Г. 8
10.Найдите десятый член арифметической прогрессии 3; 1;….
А. 21 Б. 20 В. - 15 Г. - 20
11. Найдите сумму одиннадцати первых членов арифметической прогрессии, если
а1= - 5, d= - 3
А. - 220Б. -200 В. -150 Г. -100
12. Найдите первый член арифметической прогрессии, если разность равна 2, а двадцатый член этой прогрессии равен.28.
А. -5; Б, 4; В. -10; Г. 0
13. Какое из чисел является членом арифметической прогрессии, заданной формулой а n = 3n - 1.
А.13 Б. 0 В.8 Г. - 8
14. Найдите восьмой член арифметической прогрессии -3; 2;….
А. 21 Б. 32 В. - 16 Г. - 20
15. Найдите сумму пятнадцати первых членов арифметической прогрессии, если а1=4, d= - 5
А. 220Б. -275 В. -150 Г. -465
Вернуться в содержание






