| Теория | Практика |
Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и тоже число q, называется геометрической прогрессией.
Число q – знаменатель прогрессии.  ; ;  Формула n -го члена:
Формула n -го члена:  Свойство прогрессии:
Свойство прогрессии:  Сумма n -членов:
Сумма n -членов:  , ,  Если
Если  , то прогрессия называется бесконечно убывающей геометрической прогрессией. , то прогрессия называется бесконечно убывающей геометрической прогрессией.
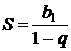
| 1. В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии.
Решение.
1) Пусть ( ) - данная геометрическая прогрессия. Составим систему ) - данная геометрическая прогрессия. Составим систему
 .
Далее: .
Далее:  , , 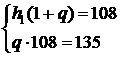 . Отсюда . Отсюда  , ,  .
2) .
2)  , ,  Ответ: 48, 60, 75.
2. (Демо 2010, Задание 19). В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии.
Решение. 1) Пусть (
Ответ: 48, 60, 75.
2. (Демо 2010, Задание 19). В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии.
Решение. 1) Пусть (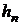 ) - данная геометрическая прогрессия. Составим систему ) - данная геометрическая прогрессия. Составим систему
 .
Далее: .
Далее:  , , 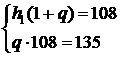 . Отсюда . Отсюда  , ,  .
2) .
2)  , ,  Ответ: 48, 60, 75.
Ответ: 48, 60, 75.
|
| Модель 1 Баллы | Критерии оценки выполнения задания |
| 4 | Ход решения верный, оба его шага выполнены, получен верный ответ. |
| 3 | Ход решения верный, решение доведено до конца, но допущена одна вычислительная ошибка и ответ отличается от правильного. |
| 0 | Другие случаи, не соответствующие указанным критериям |
| Модель 2 Баллы | Критерии оценки выполнения задания |
| 3 | Ход решения верный, оба его шага выполнены, получен верный ответ. |
| 2 | Ход решения верный, решение доведено до конца, но допущена одна вычислительная ошибка или описка и ответ отличается от правильного. |
| 1 | Верно найдены и первый член прогрессии, но решение не завершено. q Или: ход решения верный, но допущены две вычислительные ошибки или описки. |
| 0 | Другие случаи, не соответствующие указанным критериям. |
Реши сам:
1. Найдите сумму всех натуральных чисел, кратных пяти и меньших 200.
2. Сумма первых четырех членов геометрической прогрессии равна 40, знаменатель прогрессии равен 3. Найдите сумму первых шести членов этой прогрессии.
3. Найдите сумму всех натуральных чисел, кратных трем и не превосходящих 150.
4. Сумма первых трёх членов геометрической прогрессии равна 39, знаменатель прогрессии равен -4. Найдите сумму первых четырёх членов этой прогрессии.
5. В геометрической прогрессии сумма первого и второго членов равна 60, а сумма второго и третьего членов равна 84. Найдите первые три члена этой прогрессии
6. В геометрической прогрессии  ,
,  . Является ли членом этой прогрессии число 192?
. Является ли членом этой прогрессии число 192?
7.Найдите сумму всех отрицательных целых чисел, кратных трем и
больших - 170.
8.Сумма первых пяти членов геометрической прогрессии равна - 61, знаменатель прогрессии равен -3. Найдите сумму первых шести членов этой прогрессии.
9.Сумма первых трёх членов геометрической прогрессии равна 39, знаменатель прогрессии равен -4. Найдите сумму первых шести членов этой прогрессии.
10. Найдите сумму всех натуральных чисел, не превосходящих 150, которые не делятся на 5.
11. В геометрической прогрессии  ,
,  . Есть ли среди членов этой прогрессии число 144?
. Есть ли среди членов этой прогрессии число 144?
12. Найдите сумму первых шести членов геометрической прогрессии, если ее четвертый член равен  , а знаменатель равен
, а знаменатель равен  .
.
13. Найдите сумму первых шести членов геометрической прогрессии, если ее пятый член равен 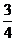 , а знаменатель равен
, а знаменатель равен  .
.
14. Сумма первого и четвертого членов геометрической прогрессии равна 36, а сумма второго и пятого членов равна 72. Сколько членов этой прогрессии, начиная с первого, нужно сложить, чтобы их сумма была равна 124?
15. Разность пятого и первого членов геометрической прогрессии равна 80, а разность шестого и второго членов равна 240. Сколько членов этой прогрессии нужно сложить, чтобы их сумма была равна 364?
Вернуться в содержание






