В силу того, что для решения задач в практике используется, в основном, десятичная позиционная система счисления, особый интерес и для математической теории представляют те дроби, знаменатель которых является какой-либо степенью числа 10, т.е. дроби вида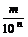 
. Дроби такого вида объединяются в одну группу, и их называют десятичными дробями.
Распространим запись натурального числа в десятичной позиционной системе счисления на дроби, имеющие знаменателем степень числа 10. Нам известно, что любое натуральное число п можно записать так: n = ak × 10 k + ak -1 × 10 k -1 + … + a 1 × 101 + a 0 × 100, где 0 £ а i £ 9, ak ≠ 0.
По аналогии с этой записью составим сумму, включив в нее и отрицательные степени числа 10, т.е.
n = ak ×10 k + ak -1 × 10 k -1 + … + a 1×101 + a 0×100+ 
(*),
где аi (i = 0, 1, …, k) и вj (j = 1, 2, …, е) – цифры, т.е. 0 £ аi £ 9 (ak ¹0) и 0 £ вj £ 9.
П р и м е р. 81,302 = 8 · 10 + 1 +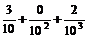 
.
Очевидно, что число n, представляющее собой сумму натуральных чисел и обыкновенных дробей, есть положительное рациональное число.
Его записывают так: n = 
, отделяя запятой целую часть от дробной.
Действительно, если в сумме (*) все слагаемые привести к одному знаменателю и сложить их как обыкновенные дроби, то получим:
,
т.е. 
Þ n × 10 е =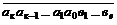 
,
значит, n · 10 е Î N и можно сделать вывод о том, что, если рассматривать обыкновенные дроби, знаменатель которых есть степень числа 10, то знаменатель в записи положительного рационального числа можно опустить, т. к. его значение точно определяется положением запятой, отделяющей цифры целой части от цифр дробной части, т.е. 
, причем сохраняется основное свойство десятичной записи числа: из каждых двух соседних цифр правая цифра имеет разрядную единицу в 10 раз меньшую, чем левая.
Таким образом, десятичной дробью называется обыкновенная дробь со знаменателем равным степени 10, записанная в десятичной позиционной системе счисления. Из этого определения вытекает два важных свойства десятичных дробей.
Свойство 1. Умножение десятичной дроби на 10 s достигается переносом запятой на s цифр вправо, а деление десятичной дроби на 10 s – переносом запятой на s цифр влево.
Действительно, если записать десятичную дробь в виде обыкновенной дроби, т.е.
,
то деление на 10 s увеличит знаменатель в 10 s раз,т.е. получится знаменатель 10 s + e , а это значит, в десятичной записи n = 
дробная часть должна содержать e + s цифр, т.е. запятая окажется перенесенной на s цифр влево. Точно так же рассматривается случай переноса запятой при умножении на 10 s.
Свойство 2. Если приписать к десятичной дроби любое число нулей справа, или отбросить нули, стоящие в конце десятичной дроби, то значение десятичной дроби не изменится.
Действительно, если к дроби вида n = приписать несколько нулей, то в записи (*) добавятся новые слагаемые вида 
, 
и так далее, которые не изменят значение исходной дроби. Если в записи дроби последними цифрами являются нули, то в записи (*) отбросятся слагаемые, равные 0, что так же не изменит значение исходной дроби.
Свойство 2 позволяет сформулировать правило приведения десятичных дробей к общему знаменателю.
Если у первой дроби после запятой стоит к цифр, а у второй s цифр, причем к < s, то для приведения этих дробей к общему знаменателю, достаточно приписать к первой дроби s – к нулей справа. Тогда у обеих дробей число цифр после запятой будет одинаковым, значит, дроби имеют один и тот же знаменатель.
Таким образом, все десятичные дроби можно считать приведенными к общему знаменателю. Поэтому десятичные дроби легко сравнивать по значению, используя правило сравнения двух обыкновенных дробей с равными знаменателями.
Правило сравнения двух десятичных дробей формулируется так: из двух десятичных дробей больше та, у которой больше целая часть. Из двух десятичных дробей с равными целыми частями больше та, у которой больше первый из неравных десятичных знаков.
П р и м е р. 102,84 > 100,93, т.к. 102 > 100.
102,84 < 102,86, т.к. 4 < 6.
Выше сказано, что все десятичные дроби можно считать приведенными к общему знаменателю, что означает, что сложение и вычитание десятичных дробей сводится к соответствующим операциям над их числителями, т.е. к сложению и вычитанию натуральных чисел.
П р и м е р. 23,45 + 11,2441 = 23,4500 + 11,2441 = 34,6941.
Сформулируем правило сложения десятичных дробей.
Для того, чтобы сложить две десятичные дроби нужно:
1) уравнять в этих дробях число десятичных знаков после запятой, приписывая к одной из них справа несколько нулей;
2) не обращая внимания на запятые, сложить полученные при этом натуральные числа;
3) в полученной сумме отделить запятой столько знаков, сколько было отделено в каждом из слагаемых.
Можно произвести сложение десятичных дробей и в «столбик», например, так:
Так как сложение десятичных дробей сводится к сложению натуральных чисел, то сложение десятичных дробей обладает свойством коммутативности и ассоциативности.
Правило вычитания десятичных дробей формулируется аналогично правилу сложения десятичных дробей.
Например, 2,35 – 1,268 = 2,350 – 1,268 = 1,082.
Можно вычитание выполнить и в «столбик».
(Нули не пишем, подразумеваем их наличие).
При выводе правила умножения десятичных дробей воспользуемся известным нам правилом умножения обыкновенных дробей:
.
Сформулируем правило умножения десятичных дробей. Для того, чтобы умножить две десятичные дроби нужно:
1) отбросить в записи данных десятичных дробей запятые;
2) перемножить получившиеся натуральные числа;
3) в произведении отделить запятой столько последних цифр, сколько их было отделено до начала умножения в первом и втором множителе вместе.
Например,
Так как правило умножения десятичных дробей является частным случаем умножения обыкновенных дробей, то умножение десятичных дробей обладает свойствами коммутативности и ассоциативности.
При выводе правила деления десятичных дробей воспользуемся правилом деления обыкновенных дробей.
Обыкновенные дроби делятся так: 
: 
= 
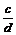, следовательно, 
: 
= 
= 
, (s > к).
Сформулируем правило деления десятичных дробей. Для того, чтобы разделить десятичную дробь на десятичную, надо:
1) в делителе перенести запятую в конец числа (отбросить ее), сделать делитель целым;
2) чтобы частное не изменилось, в делимом надо перенести запятую вправо на такое же количество десятичных знаков, какое было в делителе;
3) после этого деление производится обычным способом «углом». Запятая в частном ставится в момент использования всех цифр целой части делимого.
Например. 31,8836: 2,36.
 |
