Теорема 1 (О связи НОД и НОК). НОД (а, в) · НОК (а, в) = а · в.
Доказательство.
Пусть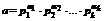 
и 
, тогда 
, используя ассоциативность и коммутативность умножения, перегруппируем множители следующим образом: а × в = 
, где d i ≤ ti, i = 1, 2, …, к.
Т.е. поступили мы так: выбрали 
и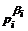 
и сравнили ai и b i. Если a i ≥ b i, то 
во 2-ой скобке, а 
– в 1-ой скобке. Но ведь тогда
,
,
т.е. а · в =НОД(а, в)·НОК(а, в).
П р и м е р.
Запишем равенство 12 ·240 = 60 · 48, получим 2880 = 2880.
Теорема 2 (облегчающая вычисление НОД и НОК).
1) НОД (а 1, а 2, … а n) =НОД (НОД(а 1, а 2), а 3, …, аn),
2) НОК (а 1, а 2, … а n) =НОК (НОК(а 1, а 2), а 3, …, аn).
Теорема позволяет при отыскании НОД и НОК нескольких чисел производить это последовательно, заменяя пару чисел их НОД и НОК.
Доказательство. 1) Пусть даны числа а 1, а 2, …, аn своими каноническими разложениями.
,
,
,
… …….. …….
.
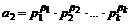НОД (а 1, а 2) = 
, где ti – наименьшее из чисел a i, b i, i = 1, 2, …, к.
Обозначим через d i – наименьшее из чисел a i, b i, ci, …, g i, тогда d i является наименьшим из чисел ti, ci, …, g i.
НОД 
, отсюда
НОД(а 1, а 2, …, аn) = НОД (НОД (а 1, а 2), а 3, а 4, …, аn).
2) Точно так же доказывается и вторая часть.
НОК 
, где r i – наибольшее из чисел a i, b i, i = 1, 2, …, к.
НОК 
, где mi – наибольшее из чисел a i, b i, ci, …, g i и является наибольшим из чисел ri, ci, …, g i, отсюда
НОК (а 1, а 2, …, аn) = НОК (НОК (а 1, а 2), а 3, а 4, …, аn).
П р и м е р. Применяя теорему 2, найдем НОД (1320, 3600, 1485).
1320 = 23 · 31 · 5 · 11,
3600 = 24 · 32 · 52 ·110,
1485 = 20 · 33 · 5 · 11.
НОД (1320, 3600) = 23 · 3 · 5 = 120,
НОД (120, 1485) = 20 · 3 · 5 = 15.
Значит, НОД (1320, 3600, 1485) = 15.
НОК (1320, 3600) = 24 · 32 · 52 · 11 = 39600
НОК (39600, 1485) = 24 · 33 · 52 · 11 = 118800.
Значит, НОК (1320, 3600, 1485) = 118800.
Теорема 3. Пусть m – некоторое натуральное число, тогда
НОД (ma1, ma2, …, man) = m НОД (а 1, а 2, …, аn),
НОК (ma1, ma2, …, man) = m НОК (а 1, а 2, …, аn), то есть общий множитель можно выносить за знак НОД и за знак НОК.
Доказательство. Запишем каноническое разложение чисел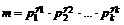 
,
НОД (а 1, а 2, …, аn) = 
, НОК (а 1, а 2, …, аn) = 
. Ясно, что 
есть наименьший, а 
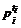– наибольший среди степеней простого числа pi, встречающихся в канонических разложениях чисел а 1, а 2, …, аn, но тогда 
будет наименьшим, а 
– наибольшим среди степеней простого числа p i в разложениях чисел mа 1, mа 2, …, mаn. pi – это любое число из простых множителей чисел а 1, а 2, …, аn. Значит, получили m НОД (а 1, а 2, …, аn) =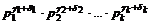 
= = НОД (mа 1, mа 2, …, mаn).
Аналогично, m НОК (а 1, а 2, …, аn) = 
= НОК (mа 1, mа 2, …, mаn).
Следствие 1.
Пусть m – есть некоторый общий делитель чисел в 1, в 2, …, вn, тогда
НОД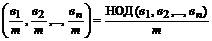 
;
НОК 
,
т.е. если данные числа разделить на m, то их НОД и НОК также разделятся на m.
Доказательство. По теореме 3 имеем:
m НОД (а 1, а 2, …, аn) = НОД (mа 1, mа 2, …, mаn), разделим обе части равенства на m, получим
НОД (а 1, а 2, …, аn) = 
.
Обозначим mai = вi Þ ai = 
. Тогда:
. Что и требовалось доказать. Точно также выводится равенство относительно НОК.
Следствие 2.
d = НОД (а 1, а 2, …, аn)Û 
.
Доказательство. Необходимость.
Дано НОД (а 1, а 2, …, аn) = d, доказать, что 
.
По следствию 1, имеем
НОД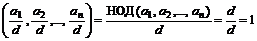 
.
Достаточность.
Дано НОД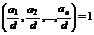 
, доказать, что НОД (а 1, а 2, …, аn) = d.
Обе части данного равенства умножим на d,
тогда d НОД 
.
По теореме 2 НОД (а 1, а 2, …, аn) = d. Что и требовалось доказать.
П р и м е р ы на применение следствия.
Пусть в1 = 33, в2 = 55, в3 = 99 Þ m = 11
1. 
.
=НОК (3, 5, 9) Þ НОК (33, 55, 99) = 11 · 45 = 495.
2. Пусть в 1 = 33, в 2 = 55, в 3 = 99;
НОД (33, 55, 99) = 11. Тогда НОД (
)= 1.
