Действия над натуральными числами – мерами величин

В нижеследующих определениях будем считать, что числа p, q Î N, а, в, с – отрезки, е – единичный отрезок.

Определение суммы натуральных чисел.

р + q = m_е (а), если а = в + с, m_е (в) = р, m_е (с) = q.

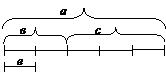Таким образом, сумму двух натуральных чисел определяют через длину суммы отрезков в и с (рис. 1).

 

 

Рис. 1

р + q = n (В   С), если В С = Æ.   n (В) = р. n (С) = q.

Аналогия с теоретико-множественным подходом представлена на рис 2.

B                   C

        

р _эл.                 q _эл.

 

       Рис. 2

Замечание. Здесь и далее в этом параграфе «эл» – это сокращение слова «элементов».

Определение разности натуральных чисел.

р – q = m_е (с), если а = в + с, m_е (а) = р, m_е (в) = q.

Таким образом, разность двух натуральных чисел определяют через длину «разности» двух отрезков а и в.

p – q = n (A\B),если В Í А, n (A) = p, n (B)= q.

Аналогия с теоретико-множественным подходом представлена на рис. 3.

А

р_эл.                      А \ В

                   (? = эл)

  Рис. 3

Определение произведени я натуральных чисел.

p · q = т_{е 1} (а), если т_{е 1} (е) = р, т_e (а) = q, е ₁ – новый единичный отрезок (рис. 4).

 

                       а

               Рис. 4

Таким образом, умножение натуральных чисел отражает переход к новой (более мелкой) единице длины е ₁ по сравнению со старой единицей длины е.

Аналогия с теоретико-множественным подходом представлена на рис 5.

p · q = n (A ₁ A ₂ ... A_q),

если A_i A_j =Æ (i ≠ j).

n (А ₁) = n (А ₂) =... = n (A_q) = p.

                                                                                  Рис. 5

Определение частного натуральных чисел.

1 случай. p: q = т_{е 1} (а), если т_е (а) = р, т_е (е ₁) = q; т_{е 1} (a) Î N, т.е. в отрезок а отрезок е ₁ укладывается целое число раз (рис. 6).

2 случай. р: q = т_е (е ₁), где т_е (а) = р, т_{е 1}(a) = q, m_e (е ₁) Î N (рис. 7).

a Рис. 6	a Рис. 7

Единичный отрезок е ₁ не задан, он получается в результате дробления отрезка а на q равных отрезков.

Таким образом, деление натуральных чисел связано с разбиением отрезка и отражает переход к новой (более крупной) единице длины е ₁, по сравнению со старой единицей длины е.

Аналогия с теоретико-множественным подходом представлена на рисунках 8, 9.

1 случай. Множество А, в котором р элементов, разбито на q равночисленных подмножеств А ₁, А ₂,..., А_q, в каждом из которых по q элементов.

Тогда р: q = n, где n – число подмножеств разбиения. Т.е. 1 случай – это задача на нахождение числа подмножеств разбиения.

 

                                                     Рис. 8

2 случай. Множество А, в котором р элементов, разбито на q равночисленных подмножеств А ₁, А ₂,..., А_q. Тогда р: q = n, где n – число элементов в каждом из подмножеств разбиения.

Т.е. 2 случай – это задача на нахождение числа элементов в подмножествах разбиения.

 

Контрольные вопросы и упражнения

1. При каких условиях натуральное число n называют мерой отрезка а?

2.  Какова общая схема решения задач, связанных с обоснованием выбора арифметического действия?