Определение. Говорят, что число а делится на число в, если существует такое число c Î N 0, что а = в · с.
В том случае, когда а делится на в пишут: а 
в. Читают: «а делится на в»; «а кратно в»; «в – делитель а». Например, 12 делится на 6, так как существует такое с = 2, что 12 = 6 · 2, иначе 12 
6.
Замечание. Записи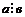 
и а: в не равносильны. Первое обозначает, что между числами а и в имеет место отношение делимости (возможно нацело число а разделить на число в). Второе – есть обозначение частного чисел а и в.
Отношение делимости обладает рядом свойств.
1°. Нуль делится на любое натуральное число, т.е.
(" в Î N) [0 в ].
Доказательство. 0 = в · 0для любого в, отсюда по определению следует, что 0 в.
2°. Ни одно натуральное число не делится на нуль, т.е. (" а Î N) [ а 
0].
Доказательство (от противного). Пусть существует c Î N 0, такое, что а = 0· с, но по условию а ≠ 0,значит ни при каком с это равенство не выполняется. Значит, наше предположение о существовании с было неверным и а 0.
3°. Любое целое неотрицательное число делится на единицу, т.е.
(" а Î N) [ а 1].
Доказательство. а = 1· а => а 1.
4°. Любое натуральное число делится само на себя (рефлексивность), т.е.(" а Î N) [ а а ].
Доказательство. а = а · 1Þ а а.
5°. Делитель в данного натурального числа а не превышает этого числа, т.е. (а в Ù а > 0) Þ (а ≥ в).
Доказательство. Так как а в, то а = в · с, где c Î N 0. Определим знак разности а – в.
а – в = вс – в = в (с – 1),поскольку а > 0, то с ≥ 1, следовательно, в (с – 1) ≥ 0,значит а – в ≥ 0 Þ а ≥ в.
6°. Отношение делимости антисимметрично, т.е.
(" a, в Î N 0)[(a в Ù в а) Þ а = в ].
Доказательство.
1 случай. Пусть а > 0, в > 0,тогда имеем:
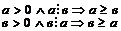(по свойству 5°). Значит, а = в.
2 случай. Пусть хотя бы одно из чисел а или в равно 0.
Пусть а = 0, то в = 0по 2°, т.к. иначе в не могло бы делиться на а. Значит а = в.
7 °. Отношение делимости транзитивно, т.е.
(" a, в, с Î N 0) [(a в Ù в с)Þ а с ].
Доказательство. а в Þ ($ к)[ а = вк ]; в с Þ ($ ℓ)[ в = cℓ ].
а = вк = (сℓ) к = с (ℓк), ℓк – произведение двух неотрицательных целых чисел ℓ и к и потому само является целым неотрицательным, т.е. а с.
8°. Если каждое из чисел а и в делится на с, то их сумма а + в делится на с, т.е. (" a, в, с Î N 0) [(a с Ù в с) Þ (а + в) с ].
Доказательство, а с Þ а = ск, в с Þ в = cℓ.
а + в = ск + cℓ = с (к + ℓ), т.к. к + ℓ –целое неотрицательное число, значит (а + в) с.
Доказанное утверждение справедливо и в случае, когда число слагаемых больше двух.
Если каждое из чисел а 1,..., ап делится на с, то их сумма а 1+... + ап делится на с.
Кроме того, если числа а и в делятся на с, причем а ≥ в, то их разность а – в делится на с.
9°. Если число а делится на с, то произведение вида ах, где x Î N 0, делится на с, т.е. а с Þ (" x Î N 0)[ ax с ].
Доказательство. а с Þ а = ск, но тогда ах = скх = с (к · х), к, x Î N 0, значит ах с.
Следствие из 8°, 9°.
Если каждое из чисел а 1, а 2,..., ап делится на с, то каковы бы ни были числа х 1, х 2, ..., хn число а 1 х 1 + а 2 х 2 +... + аnхn делится на с.
10°. Если ас делится на вс, причем с ≠ 0, то а делится на в, т.е. (ас вс Ù с ≠ 0) Þ а в.
Доказательство.
ас = вс · к; ас = (вк) · с Ù с ≠ 0 Þ а = вк => а в.
Признаки делимости
Встречаются задачи, в которых, не производя деления, требуется установить делится или нет натуральное число а на натуральное число в. Чаще всего такие задачи возникают, когда число а надо разложить на множители. В подобных задачах пользуются признаками делимости. Признак делимости – это предложение, позволяющее ответить на вопрос, делится или нет некоторое число на данный делитель, не производя самого деления.
Применяя признак делимости, делить все-таки приходится, конечно. Из школы хорошо известен признак делимости числа на 3. Делится ли число 531246897 на 3? Для ответа на вопрос определим сумму цифр этого числа 5 + 3 + 1 + 2 + 4 + 6 + 8 + 9 + 7 = 45, т.к. 45 делится на 3, то данное число делится на 3.
Итак, вопрос о делимости данного натурального числа сведен к вопросу о делимости меньшего натурального числа.
Признаки делимости зависят от системы счисления. Рассмотрим некоторые признаки делимости в десятичной системе счисления.
