Ранее было дано аксиоматическое определение умножения целых неотрицательных чисел.
В начальной школе используется подход к определению умножения, основанный на понятии суммы одинаковых слагаемых.
Теорема 1. Если в > 1, то произведение чисел а и в равно сумме в слагаемых, каждое из которых равно а.
Доказательство. Обозначим сумму в слагаемых, каждое из которых равно а, через а · в и, кроме того, положим, что а · 1 = а. Тогда, по определению суммы, имеем:
.
Значит, операция а · в подчиняется тем же требованиям, что и операция умножения, определенная ранее, а именно а · 1 = а и а · (в +1) = а · в + а. В силу единственности умножения получаем, что а · в = в · а.
Таким образом, если а и в – целые неотрицательные числа, то
а) а · в =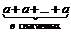 
при в > 1;
б) a · 1 = а при в = 1;
в) a · 0 = 0 при в = 0.
Для вывода законов умножения целых неотрицательных чисел удобнее другое теоретико-множественное истолкование произведения. Оно связано с декартовым произведением множеств. Рассмотрим сначала следующий пример. Найдем декартово произведение множеств А = { а, в, с } и В = { х, у }. Оно состоит из пар, которые мы запишем в виде прямоугольной таблицы.
(а, х), (а, у),
(в, х), (в, у),
(с, х), (с, у).
В каждой строке таблицы все пары имеют одинаковый первый элемент, а в каждом столбце – одинаковый второй элемент. При этом никакие две строки не имеют хотя бы одной одинаковой пары. Отсюда следует, что число элементов таблицы равно 2 + 2 + 2 = 6. С другой стороны n (А) = 3, n (В) = 2, 3 · 2 = 6. На этом примере видим, что число элементов в декартовом произведении двух конечных множеств равно произведению чисел элементов в этих множествах.
Теорема 2. Пусть А и В – конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство n (А × В) = n (А) · n (В).
Доказательство. Пусть А = { а 1, а 2,..., аq }, В = { в l, в 2, в 3,..., вk }, причем k > l. Составим декартово произведение А × В и запишем в виде таблицы:
(а 1, в l), (а 1, в 2), (а 1, в 3),..., (а 1, в k),
(а 2, в 1), (а 2, в 2), (а 2, в 3),..., (а 2, в k)
… … … … …
(аq, в 1), (аq, в 2), (аq, в 3),..., (аq, вk).
Число элементов в первой строке равно k, т.к. это элементы вида (a 1, вi), где 1 ≤ i ≤ k и т.д. в строке с номером q число элементов равно k. Всего 
элементов в таблице.
Сумма q слагаемых, каждое из которых равно k, это есть k · q. Итак, n (А × В) = k · q = n (А) · n (В). При k = 1, множество В содержит один элемент и число элементов декартова произведения равно q · 1 = q.
При k = 0 В = Æ, тогда q · 0 = 0.
Свойства умножения:
1°. Коммутативность. (" a, в Î N 0)[ a · в = в · а ].
Так как А × В ~ В × А, то n (А × В) = n (В × А).
2°. Ассоциативность. (" a, в, с Î N 0) [(a · в) · с = а · (в · с)].
Так как (А × В) × С ~ А × (В × С) Þ n ((А × В) × С) = n (А × (В × С)).
3°. Дистрибутивность относительно сложения.
(" a, в, с Î N 0) [(а + в) · с = а · с + в · с ].
Так как (A 
B) × C ~ (A × C) (B × C), то
n ((A B) × C) = n ((A × C) (B × C)).
Контрольные вопросы и упражнения
1. Используя теоретико-множественное истолкование вычитания и его свойств, решите следующие примеры из начального курса математики:
а) 48 – 30; б)12 – 5; в) (17 – 2) – 5;
г) 84 – (70 – 16); д) 24 + (76 – 28).
2. Сформулируйте определение произведения целых неотрицательных чисел через декартово произведение множеств и, используя его, объясните, что:
а) 3 · 4 = 12; б) 4 · 1 = 4; в) 4 · 0 = 0.
3. Обоснуйте различные способы решения следующей задачи:
В вазе лежало 6 яблок и 4 апельсина, их нужно разделить между двумя детьми. Сколько фруктов получил каждый ребенок?
