Перечислим свойства вычитания и дополнения.
Для любых множеств А, В, С:
1°. 
= U,
2°. 
= Æ,
3°. А \ Æ = А,
4°. 
= A,
5°.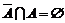 
,
6°. 
,
7°. А \ (В 
С) = (А \ В) \ С,
8°. А \ (В \ С) = (А \ В) С, если С Í А,
9°. 
,
10°. 
,
11°. (А \ В) В = А, если В 
А,
12°. A 
B = (A \ (A 
B)) B.
Свойства 1°-6° вытекают непосредственно из определения дополнения. Приведем доказательство свойства 7°.
Пусть х Î А \ (В С) Þ х Î А и х Ï B 
Þ х Î А и х Ï B и x Ï C Þ (x Î A \ B) и (x Ï C) Þ х Î (А \ В) \ С, то есть А \ (B С) Í (А \ В) \ С.
Обратное включение доказывается точно такой же цепочкой, рассматриваемой лишь с конца.
Приведем доказательство свойства 8°.
Пусть х Î А \ (В \ С) => х Î А и х Ï В \ С. Последнее утверждение может выполняться тогда и только тогда, когда выполняется хотя бы одно из условий х Ï В или х Î С. Допустим х Ï В. Тогда (т.к. х Î А) х Î А \ В и х Î (А \ В) С. Если х Î С, то также х Î (А \ В) С.
В любом случае из утверждения х Î А \ (В \ С) следует, что х Î (А \ В) С. Значит, А \ (В \ С) Í (А \ В) С.
Пусть теперь х Î(А \ В) С, тогда х Î А \ В или х Î С. Если х Î А \ В, то х Î А и х Ï В. Значит, х Î А и x Ï В \ С. Следовательно, х Î А \(В \ С) и в этом случае из х Î (А \ В) С следует, что х Î А \ (В \ С). Если же х Î С, то (по условию С Í А) х Î А. Кроме того, х Ï В \ С, т.к. х Î С. Следовательно, и в этом случае из утверждения х Î (А \ В) С следует утверждение х Î А \ (В \ С). Поскольку других возможностей нет, то в любом случае (А \ В) С Í A \ (B \ C). Учитывая первое включение, получаем, что эти множества совпадают.
Свойства 9° и 10° называются законами двойственности де Моргана[2].
Приведем доказательство свойства 9°.
Пусть x Î 
=> 
и 
и 
. Значит, 
. Обратно, пусть 
и 
=> => 
. Значит,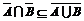 
. Итак, 
Приведем доказательство свойства 10°.
Пустъ 
=> 
=> или 
=> 
или => 
. Значит, 
.
Обратно пусть 
или 
или 
. Значит, 
.
Итак,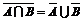 
Приведем доказательство свойства 11°.
Пусть х Î (А \ В) В, тогда х Î А \ В или х Î В. Если х Î В, то
х Î А в силу условия В А. Если же х Î А \ B то х Î А по определению разности множеств. В любом случае х Î А, т.е. (А \ В) В А. Докажем обратное включение. Пусть х Î А. Если х Î B, то х Î(А \ В) В. Если же х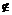 
B то х 
А \ В. В любом случае х Î (А \ В) В и включение А (А \ В) В также доказано.
Приведем доказательство свойства 12°.
Пусть х Î A В. Если х Î В, то х Î (А \(А B)) B. Если х Ï B, то х Ï A B, с другой стороны х Î A B, следовательно х Î A. Значит, х Î А \ (A В). И в этом случае х Î (А \ (А В)) В.
Докажем обратное включение. Пусть х Î (А \ (А В)) В. Тогда х Î А \ (А В) или х Î В. Если х Î B, то х Î A B, если же х Î А \ (А В }, то х Î А. В любом случае х Î A B.
Лекция 4 Тема: Декартово умножение множеств
План:
§ 1. Декартово умножение множеств
§ 2. Разбиение множества на классы
