Важную роль в принципе максимума играют вспомогательные переменные ψ0 (t), ψ1 (t) ,…, ψn (t) и функция Н, называемая гамильтонианом
(5.42)
Функции ψi (t) определяются из дифференциальных уравнений
(5.43)
Если в (5.43) подставить функцию Н (5.42), то получим систему дифференциальных уравнений относительно функций ψi (t)
(5.44)
Теперь сформулируем основную теорему принципа максимума:
Оптимальное управление и (t) с координатами u1(t),…,ur(t), доставляющее минимум функционалу J (55.2), одновременно обеспечивает максимум гамильтониану Н (5.42) при условии, что существует ненулевая непрерывная функция ψ (t) с координатами ψ1(t),…, ψr(t), удовлетворяющими уравнениям (5.43), т.е.
Особенностью принципа максимума является то, что вариационная задача нахождения функции и (t), доставляющей экстремум функционалу J, заменена гораздо более простой задачей математического анализа нахождения параметра и, доставляющего максимум вспомогательной функции Н (и).
Прежде чем перейти к примерам, наметим план решения задачи с помощью принципа максимума:
1. Записываем уравнения объекта в виде системы уравнений первого порядка (5.41), не забыв уравнения для функционала (5.40):
2. Составляем функцию гамильтониана Н:
3. Определяем значение и, максимизирующее Н, из системы уравнений
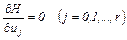(5.45)
Возможно, что максимум Н достигается на границе допустимой области управлений, тогда для некоторых j равенство (5.45) может не выполняться при ненулевой функции ψ (t).
В уравнениях (5.45) для определения и (t) содержится (2n+r+2) неизвестных: (n+1) функций уi (t), (n+1) функций ψi (t), и r функций uj (t). Для их определения имеются r уравнений (5.45), (п+1) уравнений исходной системы (5.41) и осталось составить еще (n+1) уравнений для функций ψi (t) вида (5.43).
4. Составляем уравнения (5.43) для определения ψi (t):
Из совместного решения названных (2n+r+2) уравнений находим оптимальное управление и (t).
Вопросы и задания
1. Какие возможности в решении задач оптимального управления реализованы в принципе максимума Понтрягина?
2. Какие исходные данные и в каком виде должны быть представлены перед использованием принципа максимума?
3. Сформулируйте основную теорему принципа максимума.
4. Сформулируйте план решения (алгоритм) решения задач с помощью принципа максимума Понтрягина.
5.9. Оптимальное управление объектом 2-го порядка
при ограничении на величину сигнала управления
Определим оптимальное по быстродействию управление объектом, который описывается дифференциальным уравнением 
, при ограничении на управление | u | ≤ 1: "объект должен быть переведен из состояния у (0) в состояние у (Т) за минимальное время Т ".
Уравнение после введения обозначений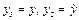 
преобразуется к системе уравнений первого порядка, что необходимо для применения принципа максимума,
(5.46)
Функционалом является время процесса 
, поэтому дифференциальное уравнение для функционала (5.40) имеет вид
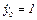(5.47)
Добавляя (5.47) к (5.46), получим полную исходную систему уравнений объекта
Примем, для определенности поиск такого управления u, которое переводит систему из состояния у10=у1 (0) и у20=у2 (0), в котором хотя бы одна координата у10 или у20 не равна нулю, в состояние у1Т=у1 (Т) =0 и у2Т=у2 (Т) =0, т.е. из произвольной точки { у10 ,y20 } в начало координат фазовой плоскости { у1 ,y2 }.
Составляем функцию гамильтониана
(5.48)
В (5.48) только последнее слагаемое зависит от u, поэтому можно обеспечить максимальное значение Н, добившись максимума этого слагаемого, т.е. необходимо, чтобы
(5.49)
Для определения u, удовлетворяющего условию (5.49), составим уравнение (5.45)
которое удовлетворяется только при ψ2 (t) =0. Однако в формулировке принципа максимума требуется существование ненулевой функции ψ2 (t), т.е. не допускается равенство ψ2 (t) =0 для всех t. Отсюда следует, что значения u, максимизирующие (5.49), следует брать на границах, т.е. подавать либо u=+1 либо u=-1. Очевидно, что для максимизации Н при ψ2 (t) >0 следует брать u=+1, а при ψ2 (t) <0 необходимо u=-1. Этот закон управления можно записать с помощью функции sign:
(5.50)
Для определения функций ψi (t)составим систему уравнений типа (5.43)
Решения этих уравнений имеют вид
(5.51)
Подставляя (5.51) в (5.50), получим окончательно
(5.52)
Так как функция ψ2=С2-С1·t может менять знак не более одного раза, то оптимальное управление (5.50) и, соответственно, (5.52) представляет собой кусочно-постоянную функцию, принимающую предельные значения +1 или -1 и имеющую не более двух интервалов постоянства. Управляющие последовательность могут быть одного из четырех типов: u= { -1 }; u= { +1 }; u= { -1, +1 }и u= { +1, -1 }.
Итак, применение принципа максимума позволило ответить на основной вопрос: каким должно быть по форме оптимальное управление u. Конкретный вид зависимости может быть найден либо после определения постоянных С1 и С2, входящих в выражение (5.52), либо после решения системы уравнений (5.46) объекта. Второй путь, как правило, проще.
Общее решение системы (5.46) имеет вид
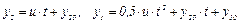(5.53)
После исключения из системы (5.53) времени t, получим фазовое уравнение
(5.54)
Фазовыми траекториями являются параболы (рис.5.13). Траектории 1-0-2, проходящие через конечную точку с координатами у1Т=0 и у2Т=0 (рис.5.14), имеют в согласно (5.54) вид
Если начальная точка {у10 , у20} находится на участке 0-1 (точка М1 на рис.5.14), то достаточно одного значения сигнала u=-1, а на участке 0-2 (точка М2) – сигнала u=+1.
Другие начальные точки могут располагаться либо над линией 1-0-2, либо под ней. Для точек типа М3 над линией 1-0-2 нужно сначала подать u=-1, а в точке М4 переключить на u=+1. Для точек типа М5 под линией 1-0-2 нужно сначала подать u=+1, а в точке М6 переключить на u=-1. Таким образом, линия 1-0-2 является линией переключения на фазовой плоскости управляемой системы.
Линия переключения состоит из отрезков двух парабол, соответствующих значениям u=+1 и u=-1, ее уравнение имеет вид
При 
нужно подать управляющий сигнал u=-1, а при 
- подать u=+1. Обобщая эти условия выбора вида сигнала: u=-1 или u=+1, - алгоритм формирования u можно записать в виде
Структурная схема оптимальной по быстродействию САУ приведена на рис.5.15.
Функциональный блок F (y2) вычисляет сигнал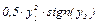 
, который складывается с сигналом у1. Затем формируется сигнал со знаком обратным знаку сигнала этой суммы, который поступает на идеальное двухпозиционное реле. Сигнал u на выходе реле принимает два значения -1 или +1. Объект управления представлен в виде двух последовательно соединенных интегрирующих звеньев.
Таким образом, оптимальная по быстродействию САУ оказалась нелинейной, в которую вошли два нелинейных звена – компаратор и функциональный блок F (y2).
На основе рассмотренного примера можно заметить, что функцию 
, а следовательно, и ψ0 (t) можно не включать в выражение для Н, если функционал не содержит в явном виде управления и, так как в этом случае слагаемое ψ0·f0 не влияет на максимизацию гамильтониана Н.
Вопросы и задания
1. Как получено выражение Гамильтониана для рассматриваемой САУ?
2. Как определен оптимальный закон изменения управляющего сигнала?
3. Как рассчитаны и построены фазовые траектории оптимальной САУ?
4. Поясните работу оптимальной САУ по ее структурной схеме.
5.10. Оптимальное управление синхронными
генераторами электростанции
по критерию устойчивости
В электрической системе, содержащей генераторы и нагрузку (рис.5.16), в установившемся режиме механический момент МД, развиваемый дизелем, уравновешивается моментом сопротивления МГ генератора. Момент сопротивления МГ определяется через электрические параметры генератора по формуле
(5.55)
При коротком замыкании (в фидере F1), включении или выключении мощных электропотребителей (в фидере F2) и т.п. из-за кратковременного неравенства моментов МД и МГ возникают большие изменения угла нагрузки θ генераторов. Если разность углов нагрузки отдельных генераторов станет равной 180О, то это является выпадением генераторов из синхронизма - тяжелейшей и опасной аварийной ситуацией, требующей немедленного отключения генераторов от сети, т.е. развалу сети электроснабжения. Ограничить в переходных режимах изменения углов нагрузки при сохранении равенства моментов МД и МГ можно, как видно из (5.55), путем соответствующего изменения э.д.с. Е генераторов, воздействуя на напряжения их возбуждения uB. Идеальным считается такое регулирование возбуждения, когда во всех режимах значение угла нагрузки отличается от номинального значения (θНОМ≈20О) на ±10О.
Для определения оптимального управления напряжением возбуждения uB, обеспечивающем быстрейшее возвращение в синхронный режим, применим принцип максимума.
Напряжение возбуждения uB ограничено снизу значением 0, а сверху – напряжением форсировки, равным 2...2,5 крат номинального возбуждения. Выбором системы отсчета можно привести напряжение возбуждения в относительных единицах к диапазону 
.
Переходные процессы в синхронном генераторе описываются семью дифференциальными уравнениями Парка-Горева относительно потокосцеплений Ψd, Ψq, Ψ1d, Ψ1q, ΨB обмоток, скольжения s и угла нагрузки θ.
(5.56)
Пятое дифференциальное уравнение является уравнением цепи обмотки возбуждения. Напряжение uB входит в него линейно, что является существенным для дальнейшего решения задачи оптимизации.
Критерием оптимального управления возбуждением или функционалом является время возвращения в синхронный режим
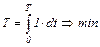(5.57)
Гамильтониан для функционала (5.57) и системы уравнений (5.56) имеет вид
,
где h0...h7 – вспомогательные функции Гамильтона.
Условием экстремума Гамильтониана Н по переменной uB является
(5.58)
Так как по теореме принципа максимума ни одна из вспомогательных функций h0...h7 не может быть тождественно равной нулю, то соотношение (5.58) невыполнимо, и максимум Н по переменной uB достигается при uB=1, если h5>0 или при uB=-1, если h5<0. Объединение этих условий выбора значения uB приводит к выражению
Следовательно, оптимальный регулятор возбуждения uB должен быть релейным, осуществляющим скачкообразный переход от –1 до +1 и обратно, т.е. чередование интервалов форсировки и полного снятия возбуждения. Для определения моментов чередования значений uB необходимо рассчитать h5 как функцию времени, решив систему сопряженных уравнений, состоящую из уравнений системы (5.56) и следующих уравнений:
Получить решение сопряженной системы уравнений чрезвычайно сложно хотя бы по одной причине – для вспомогательных функций h0...h7 не заданы начальные условия.
Однако знание вида оптимального закона управления возбуждением, как следует из изложенного выше – релейного, является решающим фактом, так как он не очевиден. Далее можно даже экспериментально определить моменты переключения напряжения возбуждения.
Вопросы и задания
1. Поясните физические процессы в электростанции, происходящие с момента короткого замыкания в сети. В чем суть проблемы обеспечения устойчивости?
2. Поясните математическую постановку задачи оптимального управления генераторами по критерию устойчивости электростанции.
3. Каким является оптимальное управление и какие возникают проблемы при его реализации?
6. АДАПТИВНЫЕ САУ
6.1. Назначение и классификация адаптивных САУ.
Структура и принцип действия
самонастраивающихся систем
Термин "адаптация" заимствован теорией управления из биологии, где им обозначают свойство приспособления организма к изменениям внешней среды. Так как элементы приспособления или адаптации существуют в любой автоматической системе, как в замкнутой, так и разомкнутой, то для выделения класса адаптивных систем необходимо дать характеристику тем условиям или требованиям, которые предъявляются к автоматическим системам управления и не могут быть качественно разрешены традиционными методами неадаптивного управления.
Прежде всего необходимость в адаптивных системах управления возникает в связи с значительным усложнением решаемых задач управления, причем специфическая особенность такого усложнения заключается в отсутствии практической возможности для подробного изучения и описания процессов, протекающих в управляемом объекте.
Неадаптивные методы управления, как правило, предусматривают наличие достаточного объема априорных сведений о внутренних и внешних условиях работы объекта еще на предварительной стадии разработки системы, которые затем используются при проектировании автоматической системы. Чем полнее априорная информация о характеристиках системы и условиях ее работы, тем обычно выше качество неадаптивного управления. В неадаптивныхсистемах неполнота информации, необходимой для управления в заданном смысле, существенно не мешает достижению цели управления, и поэтому можно не предусматривать автоматического пополнения информации в системе. Системы без пополнения информации известны давно — это обычные системы стабилизации, следящие, которые были рассмотрены в предыдущих главах.
Адаптивные системы управления работают в принципиально иных условиях, т. е. адаптивные методы способствуют достижению высокого качества управления при отсутствии достаточной полноты априорной информации о характеристиках управляемого процесса или в условиях неопределенности.
Вполне очевидно, что по мере усложнения задач, возлагаемых на автоматические системы управления, указанная неопределенность растет, т. е. становится все сложнее заранее определять характер изменения динамических свойств системы и управляемого процесса. Поэтому трудности в обеспечении надлежащего качества управления также возрастают по мере уменьшения объема априорных знаний о системе.
Благодаря адаптивным методам управления найдены достаточно эффективные способы преодоления указанных трудностей.
Эффект приспособления к изменяющимся условиям в адаптивных системах достигается за счет того, что часть функций по получению, обработке и анализу недостающей информации об управляемом процессе осуществляется уже не проектировщиком на предварительной стадии, а самой системой в процессе ее нормальной эксплуатации.
Такой частичный перенос функций способствует не только более полному использованию рабочей информации (совокупности данных о состоянии системы, получаемой непосредственно в процессе управления) при формировании управляющих воздействий, но и позволяет существенно снизить влияние неопределенности на качество управления, компенсируя в определенной степени недостаток априорного знания проектировщика об управляемом процессе.
Таким образом, к адаптивному управлению приходится обращаться тогда, когда сложность управляемого процесса достигает такого уровня, при котором влияние неопределенности или "неполноты" априорной информации об условиях работы системы становится существенным для обеспечения заданного качества процессов управления.
Поскольку адаптивные системы широко используют рабочую информацию для анализа динамического состояния системы управления и организации контролируемых изменений свойств, параметров, управляющих воздействий и структуры системы управления, то в зависимости от способов реализации контролируемых изменений в процессе нормальной эксплуатации системы можно провести следующую классификацию адаптивных систем: самонастраивающиеся системы, системы с адаптацией в особых фазовых состояниях и обучающиеся системы (рис.6.1).
Самонастраивающиеся системы (СНС) характеризуются наличием специальных контуров самонастройки, с помощью которых оцениваются динамические и статические свойства системы и формируются такие контролируемые воздействия, что система самопроизвольно приближается к определенному эталону, часто задаваемому математически в виде критерия качества функционирования. При этом контур самонастройки служит для изменения параметров или структуры основного контура с целью обеспечения заданного критерия качества управления. Обычно критерий качества управления выражается в виде функционала или функции от параметров и измеряемых координат системы. В процессе работы системы значение функционала качества изменяется и задача контура самонастройки сводится к обеспечению экстремального (минимального или максимального) значения критерия. Нахождение и поддержание экстремального значения критерия качества управления может производиться или с помощью пробных отклонений системы, или путем аналитического определения условий экстремума. В зависимости от указанных способов нахождения экстремума самонастраивающиеся системы подразделяют на поисковые и беспоисковые. В свою очередь, поисковые самонастраивающиеся системы в зависимости от применяемых методов поиска делят на системы со случайным поиском, с поиском по методу Гаусса-Зайделя, с поиском по методу градиента, с поиском по методу наискорейшего спуска. В классе беспоисковых СНС можно выделить самонастраивающиеся системы, использующие информацию о частотных характеристиках, СНС с контролем временных характеристик и границы устойчивости, СНС с эталонными моделями, градиентные СНС.
Системы с адаптацией в особых фазовых состояниях используют особые режимы или свойства нелинейных систем, например режимы автоколебаний, скользящие режимы для организации контролируемых изменений динамических свойств системы управления. Специально организованные особые режимы в таких системах либо служат дополнительным источником рабочей информации об изменяющихся условиях функционирования системы, либо наделяют систему управления новыми свойствами, за счет которых динамические характеристики управляемого процесса поддерживаются в желаемых пределах независимо от характера возникающих при функционировании изменений. Эти системы можно подразделить на релейные автоколебательные системы, адаптивные системы с переменной структурой и со скользящими режимами.
Обучающиеся системы управления характеризуются наличием специальных процессов обучения, которые заключаются в 
постепенном накапливании, запоминании и анализе информации о поведении системы и изменении законов функционирования в зависимости от приобретаемого опыта. К процессу обучения приходится прибегать тогда, когда не только мал объем априорных сведений об объекте, но и отсутствует возможность установления детальных причинно-следственных связей в структуре самой системы из-за ее сложности.
Накопление и обобщение информации в процессе обучения можно осуществлять за счет внесения «эталонного опыта» в систему извне либо путем формирования такого опыта внутри системы. Например, в первом случае обучаемой системе предъявляют последовательность ситуаций, образов или режимов, которые имеют заранее известные характеристики или различаются по принадлежности определенным классам. Поведение системы в ответ на такую обучающую последовательность ситуаций формируют на основе принципа «поощрение— наказание», т. е. правильная реакция системы на предъявленную ситуацию запоминается и используется для организации контролируемых изменений динамических свойств системы управления. В зависимости от способов накопления опыта указанные системы разделяют на обучающиеся с "учителем" и обучающиеся без "учителя" (самообучающиеся) системы.
В данном разделе курса лекций подробно рассмотрены самонастраивающиеся системы поискового и беспоискового типов.
Структурная схема самонастраивающейся системы управления представлена на рис.6.2. К основному контуру управления, состоящему из классического (неадаптивного) регулятора KР и объекта управления ОУ, добавлен блок адаптации БА, с помощью которого осуществляется коррекция параметров и алгоритма работы классического регулятора.
Основная задача самонастраивающейся системы заключается в поддержании вблизи экстремума значение функционала J, который выступает мерой качества работы системы при всех возможных изменениях входных управляющих воздействий х (t), возмущающих воздействий g (t), a также динамических характеристик объекта. Такие адаптивные системы называются также экстремальными.
Так как значение функционала качества J изменяется при действии указанных сигналов, то для выполнения основной задачи возникает необходимость в определении условий экстремума.
Если время, требующееся для определения условий экстремума, не является критическим фактором, например в случае сравнительно медленного изменения значений функционала качества в процессе управления, тогда целесообразно применять для определения условий экстремума поисковые методы.
Беспоисковые методы определения условий экстремума не требуют специальных затрат времени на поисковые движения и используют, как правило, аналитические методы определения указанных условий.
Сравнивая поисковые и беспоисковые самонастраивающиеся системы, можно сказать, что для определения условий экстремума поисковые системы нуждаются в меньшей информации, но требуют много времени на поиск, а беспоисковые системы высоким быстродействием, но требуют более полной информации об управляемом процессе.
Наиболее часто автоматический поиск применяется в системах управления, где статические характеристики объектов имеют экстремальный характер и задачей управления является нахождение и поддержание управляющих воздействий, обеспечивающих экстремальное значение управляемой величины. Когда автоматический поиск применяется для управления объектами с экстремальными характеристиками, соответствующие поисковые системы обычно называют экстремальными системами.
Идею автоматического поиска можно рассмотреть на примере определения управляющего воздействия и = и*, обеспечивающего экстремум (для определенности примем максимум) выходной величины у=у* одномерного объекта со статической характеристикой у (и). По значению у в одной точке статической характеристики объекта (рис.6.3) нельзя определить направление изменения и, соответствующее желаемому направлению изменения у. Когда текущему состоянию системы соответствует левая ветвь характеристики (точка А), величину и следует увеличить, а если текущему состоянию системы соответствует точка В, то и следует уменьшать.
Пусть система находится в точке А. Для определения правильного направления движения управляющее устройство может, например, выполнить следующие операции: вначале автоматически измерить и запомнить величину J (иА), изменить и на величину Δи и вновь измерить и запомнить у при и=иА+Δи. После этого, определяя ΔJ=J (иА + Δи)- J (иА), управляющее устройство вырабатывает рабочее воздействие, изменяющее состояние объекта в желаемом направлении.
