Расчеты статической ошибки εСТ регулирования 5 страница

а). Область правее ЛП с и=и_т. Именно в этой области задана точка с начальными условиями ε₀ и . Алгебраическое фазовое уравнение согласно (3.18) имеет вид

Это прямая линия 1-2-3, проходящая через точку с координатами ε₁=ε₀ и 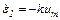, в которую САУ переходит скачком из точки 0 с начальными условиями ε₀ и . Линия 1-2-3 продлевается до ЛП, на которой ε=-ε_т.

б). Область левее ЛП с и=-и_т. Алгебраическое фазовое уравнение согласно (3.18) имеет вид

Это прямая линия 4-5, проходящая через точку с координатами ε₄=-ε_т и . Переход из точки 3 в точку 4 происходит скачком.

Линия 4-5 продлевается до ЛП, на которой ε=ε_т. Далее следует скачок в точку 2.

5. Заключение о характере переходного процесса в САУ.

Так как расчетом получена замкнутая фазовая траектория 2-3-4-5-2, то в САУ устанавливаются автоколебания. По данной циклической фазовой траектории легко рассчитать параметры автоколебаний – амплитуду А_АК и периода Т_АК. Амплитуда автоколебаний определяется непосредственно из рис.3.14

Период автоколебаний Т_АК равен сумме времен t_2-3 , t_3-4 , t_4-5 и t_5-2 движения по соответствующим участкам траектории 2-3-4-5-2. Учитываем, что движение на участках 3-4 и 5-2 происходит скачком и, поэтому, t_3-4 =0 и t_5-2=0. Ввиду симметрии участков 2-3 и 4-5 движение по ним требует одинакового времени, равного половине периода автоколебаний. Используя формулу (3.11) применительно к участку 4-5, рассчитываем полупериод автоколебаний

откуда

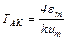
Такие же параметры А_АК и Т_АК автоколебания были рассчитаны в теме 3.1 методом припасовывания, но там расчет их был гораздо сложнее.

Вопросы и задания

1. Поясните процедуру вывода системы фазовых уравнений рассмотренной САУ.

2. Обоснуйте замкнутую форму фазовой траектории.

3. Как, используя фазовую траекторию, определить параметры автоколебаний?

 

 

3.6. Нелинейная САУ с переменной структурой

Наглядность решений, отображаемых на фазовой плоскости фазовыми траекториями дает уникальную возможность производить синтез нелинейных САУ с использованием графических возможностей фазового метода.

Рассмотрим линейную САУ 2-го порядка, изображенную на рис.3.13.

Передаточная функция замкнутой САУ имеет вид

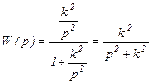
Корни характеристического уравнения чисто мнимые . С такими корнями в САУ устанавливаются незатухающие гармонические колебания (см.рис.3.5), что является признаком того, что САУ находится на грани устойчивости. Фазовой траекторией является эллипс, причем размеры полуосей эллипса зависят от величины коэффициента k (см. (3.10)): при k>1 большей полуосью является полуось по (размер полуоси по в k раз больше полуоси по у) и эллипс вытянут по вертикали, а при k<1 эллипс вытянут по горизонтали.

Из разновытянутых по осям у и эллипсов можно составить фазовую траекторию, имеющую вид сходящейся спирали (рис.3.6а).

Обозначим малый коэффициент k П-регулятора (k<1) как k_М а большой (k>1) – как k_Б. Введем в САУ логическое устройство ЛУ (рис.3.16б), осуществляющее изменение величины коэффициента передачи k П-регулятора в зависимости от сигналов состояния у и (фазовых переменных) звена 2-го порядка, которое является объектом управления.

Разработаем такое ЛУ, которое изменяло бы коэффициент k П-регулятора в соответствии с рис.3.16а:

- при ЛУ должно замыкать верхний контакт в схеме, приведенной на рис.33.2б, устанавливая большой коэффициент k_Б П-регулятора;

- при - замыкать нижний контакт, устанавливая этим малый коэффициент k_М

Так как при проверке условий и не учитывается числовое значение произведения а учитывается только знак произведения , то в основу работы ЛУ может быть положена проверка только знака произведения . Устройство для проверки знака произведения проще устройства проверки знака произведения. Для проверки знака произведения можно использовать компараторы, работа которых описывается с точностью до постоянного множителя выражениями и (см.рис.1.1).

 

Структурная схема САУ с переменной структурой (СПС), в которой подробно раскрыто логическое устройство ЛУ, приведена на рис.3.17а. При одинаковых по знаку сигналах у и выходные напряжения е₁ и е₂ компараторов К1 и К2 будут одинаковыми по величине и знаку, поэтому к обмотке реле Р будет подведено нулевое напряжение и будет замкнут его НЗ-контакт в цепи с k_Б. При противоположных по знаку сигналах у и выходные напряжения е₁ и е₂ компараторов К1 и К2 будут одинаковыми по величине, но разными по знаку, поэтому к обмотке реле Р будет подведено максимально возможное напряжение и будет замкнут его НО-контакт в цепи с k_М.

Для работы ЛУ нужны два сигнала у и . Его можно либо взять прямо из звена (рис.3.17а), либо восстановить из сигналов и или у (рис.3.17б).

График переходного процесса у_СПС в рассмотренной СПС приведен на рис.3.18. Там же приведен график незатухающих гармонических колебаний у_ЕСТ в естественной структуре (рис.3.13) при постоянном коэффициенте k.

Вопросы и задания

1. Какое свойство эллиптической фазовой траектории использовано в создании устойчивой СПС?

2. Как устанавливается алгоритм работы логического устройства в рассмотренной СПС?

3. Какова схема управляющего логического устройства и как оно работает?

 

 

3.7. Нелинейная САУ со скользящим режимом

Рассмотрим две линейные САУ 2-го порядка, изображенные на рис.3.19.

Передаточные функции этих САУ имеют вид

где знак плюс относится к схеме с отрицательной обратной связью (рис.3.19а), а знак минус – к схеме с положительной обратной связью (рис.3.19б).

Для схемы с отрицательной ОС корни характеристического уравнения чисто мнимые . С такими корнями в САУ устанавливаются незатухающие гармонические колебания (см. рис.3.5), что является признаком того, что САУ находится на грани устойчивости. Фазовой траекторией является эллипс. Для схемы с положительной ОС корни характеристического уравнения действительные и разных знаков: . С такими корнями в САУ неустойчива (см. рис.3.8). Фазовыми траекториями являются гиперболы, образующие фазовый портрет типа "седло". Таким образом, при любом знаке обратной связи САУ на рис.3.19 оказываются неработоспособными.

Введем в САУ логическое устройство ЛУ (рис.3.20а), осуществляющее переключение знака обратной связи в зависимости от сигналов состояния у и (фазовых переменных) звена 2-го порядка, которое является объектом управления.

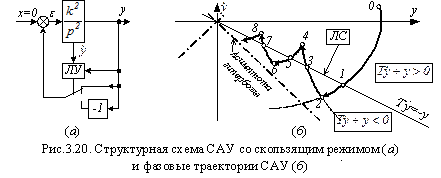
Принцип действия САУ со скользящим режимом.

На фазовой плоскости САУ отмечаются асимптоты гиперболической фазовой траектории и вводится линия переключения, она же – линия скольжения ЛС. ЛС должна располагаться относительно асимптоты и оси абсцисс так, как показано на рис.3.20б.

Пусть начальное состояние САУ задано точкой 0. ЛУ, обнаружив точку 0 над ЛС, устанавливает в САУ отрицательную ОС. Фазовой траекторией является эллипс 0-1. В точке 1 логическое устройство обнаруживает пересечение ЛС и выдает команду на изменение обратной связи на положительную. Однако из-за инерционности ЛУ такое переключение происходит с запаздыванием, пусть и небольшим. За это время САУ успевает переместиться по эллипсу в точку 2. Далее движение осуществляется по гиперболе 2-3. В точке 3 ЛУ выдает сигнал на изменение обратной связи на отрицательную. Фактически отрицательная ОС вступит в действие в точке 4. Снова движение по эллипсу 4-5-6, затем – по гиперболе 6-7-8 и т.д. В результате описанных изменений знака ОС будет происходить движение с вибрациями вдоль ЛС. При малой амплитуде забросов фазовых траекторий за ЛС (точки 2, 4, 6, 8,…) движение САУ в целом происходит по ЛС, которая описывается уравнением

(3.19)

Дифференциальное уравнение (3.19) имеет следующие принужденное, свободное и полное решения

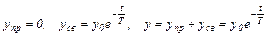(3.20)

График переходного процесса в скользящем режиме имеет вид, представленный на рис.3.21. На фоне движения в целом по экспоненте (3.20), график переходного процесса содержит колебания малой амплитуды.

Следовательно, в рассмотренной САУ со скользящим режимом осуществляется устойчивое движение по экспоненциальному закону при том, что при постоянных обратных связях исходная САУ неработоспособна.

Разработаем такое ЛУ, которое изменяло бы знак обратной связи в соответствии с рис.3.20б, а именно, если координаты у и точки фазовой траектории таковы, что:

1) точка расположена справа от оси ординат , т.е. и

2) точка расположена над ЛС, где ,

то ЛУ должно замыкать нижний контакт в схеме рис.3.20а, вводя этим отрицательную ОС.

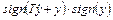Аналогично, при y>0 и одновременно при (под ЛС) логическое устройство должно замкнуть верхний контакт, вводя этим положительную ОС. Таким образом нужно проверять знак произведения или проверять знак с использованием компараторов. Структурная схема САУ со скользящим режимом с раскрытой схемой ЛУ приведена на рис.3.22.

Если выходные напряжения компараторов К1 и К2 имеют одинаковые знаки, то реле Р обесточено и сигнал обратной связи заводится через НЗ-контакт – обратная связь отрицательная. Разных знаках выходных напряжений компараторов К1 и К2 к обмотке реле приложено напряжение 2Е, реле Р включено и через замкнутый НО-контакт реле заводится положительная ОС. Для определения сигнала производной нужно применять наблюдатели, показанные на рис.3.17б.

Вопросы и задания

1. Какое свойство эллиптической и гиперболической фазовых траекторий использованы в создании устойчивой САУ со скользящим режимом?

2. Поясните принцип действия САУ со скользящим движением.

3. Как устанавливается алгоритм работы логического устройства в рассмотренной САУ со скользящим режимом движения?

4. Какова схема управляющего логического устройства и как оно работает?

 

 

3.8. Метод гармонической линеаризации.

Коэффициенты гармонической линеаризации

Метод фазовых траекторий эффективен при расчетах нелинейных САУ, порядок фазового уравнения которого не превышает 1, соответственно, порядок обыкновенного дифференциального уравнения не выше 2. При более высоком порядке дифференциального уравнения эффективными являются частотные методы. К числу таких методов относится метод гармонической линеаризации, который применяется в расчетах нелинейных САУ, в которых устанавливаются автоколебания. Метод является приближенным. С его помощью можно просто установить факт наличия автоколебаний в нелинейной САУ любого порядка и определить приближенно амплитуду А_АК и частоту ω_АК автоколебаний.

Для обоснования метода рассмотрим нелинейную САУ, со стандартной структурой, приведенной на рис.3.23. Нелинейность может быть любого вида, на рис.3.23 показана одна из возможных нелинейностей с тем, чтобы обоснование метода гармонической линеаризации было конкретным. Линейная часть ЛЧ должна быть такой, чтобы амплитудно-частотная характеристика обладала бы свойством фильтра низких частот – с увеличением частоты амплитуда выходного сигнала ЛЧ уменьшалась бы.

Пусть в нелинейной САУ существуют автоколебания. Это значит, что все сигналы САУ(ε, и и у) периодически изменяются. Реально при автоколебаниях эти сигналы изменяются не по гармоническому закону. Предположим, что выходной сигнал у САУ настолько мало отличается от синусоидального, что его можно считать гармоническим Так как ε=-у, то можно также считать сигнал ε гармоническим.

Докажем, что под таким предположением имеются веские основания. Доказательство проведем в несколько этапов.

1. Используя график нелинейности, построим график выходного сигнала и при гармоническом входном сигнале (рис.3.24).

Выходной сигнал получается периодическим, несинусоидальным, причем такой результат, очевидно, не зависит от вида нелинейности. Важно отметить, что форма выходного сигнала не зависит от частоты входного, но зависит от его амплитуды.

2. Рассчитаем спектральный состав сигнала и на выходе нелинейности.

Периодический сигнал и в разложении в ряд Фурье имеет вид

Зависимость амплитуды U_km от номера k гармоники называется спектральной характеристикой периодического сигнала. Непосредственная проверка периодических выходных сигналов для известных в ТАУ нелинейностей показал, что спектральная характеристика является падающей – чем больше номер k гармоники, тем меньше амплитуда U_km (рис.3.25а)

3. Рассчитаем спектральный состав сигнала у на выходе линейной части.

Выше было оговорено, что АЧХ линейной части является падающей типа изображенной на рис.3.25б. Амплитуды гармонических составляющих выходного сигнала у линейной части рассчитываются по формуле

В результате такого определения амплитуд Y_km как результата перемножения падающей спектральной диаграммы сигнала и и падающей АЧХ ЛЧ, спектральная диаграмма сигнала у будет резко падающей. Это значит, что в сигнале у будут малы по амплитуде не основные (высшие) гармоники и, поэтому, этими гармониками можно пренебречь. В таком случае сигнал у можно считать синусоидальным. Этим доказывается выдвинутое выше предположение о синусоидальности сигнала у.

Из полученного при доказательстве результата вытекают следующие утверждения:

1. Так как в выходном сигнале у линейной части можно пренебречь высшими гармониками, то нет смысла учитывать высшие гармоники в ее входном сигнале и. Это значит, что выходной сигнал и нелинейности можно считать гармоническим.

2. Так как при гармоническом входном сигнале ε выходной сигнал и нелинейности является гармоническим, то нелинейность в автоколебательной нелинейной САУ можно считать линейным звеном (рис.3.26), которое имеет передаточную функцию W (p) и частотную характеристику W (jω).

3. Так как вид и, следовательно, гармонический состав выходного сигнала нелинейности зависит только от амплитуды входного сигнала, то для эквивалентного описания нелинейности нужно использовать передаточную функцию W (p) и амплитудную характеристику W (A).

Для вывода передаточной функции W (p) нелинейности исключим в выходном сигнале и (рис.3.26) гармонические функции и , используя гармонические зависимости ε и . Выводим, используя входной сигнал ε:

(3.21)

Подставляем выражения гармонических функций (3.21) в выражение и:

(3.22)

Введем обозначения так называемых коэффициентов q и q' гармонической линеаризации:

(3.23)

Коэффициенты q и q' гармонической линеаризации вычисляются по формулам коэффициентов ряда Фурье. Для всех типовых нелинейностей эти коэффициенты рассчитаны и приводятся в справочниках по ТАУ. У нелинейностей любых типов всегда имеется ненулевой первый коэффициент q. Второй коэффициент q' равен нулю у однозначных нелинейностей (рис.2.1) и ненулевой только у нелинейностей, содержащих гистерезис.

Вводя обозначение производной , преобразуем (3.22) с учетом (3.23)

,

откуда эквивалентная передаточная функция нелинейности имеет вид

В соответствии с полученной передаточной функцией эквивалентная нелинейность представляет собой пропорционально-дифференциальное звено для нелинейностей гистерезисного типа и пропорциональное (q' =0) – для однозначных (безгистерезисных) нелинейностей.

Эквивалентная частотная характеристика нелинейного элемента имеет вид

(3.24)

Так как q и q' зависят (3.23) от амплитуды A входного гармонического сигнала нелинейности, то частотная характеристика (3.24) на самом деле зависит от амплитуды А и, поэтому, ее корректнее называть амплитудной характеристикой нелинейности

Вопросы и задания

1. Какие существуют показания к применению метода гармонической линеаризации?

2. Какие особенности гармонического состава сигнала на выходе нелинейного элемента и на выходе подключенного к нему линейного звена?

3. Приведите обоснование того, что в нелинейной САУ с автоколебательном режиме нелинейный элемент допустимо считать линейным звеном.

4. Что такое "коэффициенты гармонической линеаризации и как они вычисляются?

5.Приведите вывод передаточной функции нелинейного звена.

 

 

3.9. Исследование нелинейных САУ

методом гармонической линеаризации

Рассмотрим автоколебательную САУ со структурой, изображенной на рис.3.27. Если в соответствии с методом гармонической линеаризации считать нелинейный элемент линейным с передаточной функцией W_НЭ(р), то вся САУ является линейной и незатухающие гармонические колебания в ней возникнут, если САУ будет находиться на грани устойчивости. В соответствии с критерием устойчивости Найквиста САУ находится на грани устойчивости, если годограф частотной характеристики разомкнутой САУ проходит через точку с координатами (-1, j0):

(3.25)

Преобразуем (3.25)

(3.26)

и введем обозначение отрицательной обратной амплитудной характеристики нелинейности

и, поэтому, (3.27)

Слева и справа последнего равенства находятся выражения в комплексных переменных. Графическим образом левой части является частотная характеристика W_ЛЧ (jω) на комплексной плоскости, координаты точек которой зависят от частоты ω. Графическим образом правой части является отрицательная обратная амплитудная характеристика V_НЭ (A) нелинейного элемента на той же комплексной плоскости, координаты точек которой зависят от амплитуды А. Равенству графически соответствует пересечение указанных годографов (рис.3.28).

В точках пересечения по годографу W_ЛЧ (jω) определяется возможная частота автоколебаний, а по годографу V_НЭ (A) определяется возможная амплитуда автоколебаний. Можно доказать, что действительным автоколебаниям соответствует та точка пересечения годографов, после которой годограф V_НЭ (A) уходит в бесконечность. Такой точкой на графике является точка б. Значит, в рассмотренном на рис.3.28 примере в САУ устанавливаются автоколебания с частотой ω₃ и амплитудой А₄. В точке а при параметрах ω₅ и амплитудой А₂ колебательный процесс не является устойчивым и он либо затухает, либо расходится.

Графический метод определение параметров автоколебаний в нелинейной САУ является универсальным и позволяет найти решение при передаточных функциях линейной части любого порядка. Для САУ с малым порядком передаточной функции линейной части (не выше 2-го порядка), возможно аналитическое решение уравнения (3.27).

Рассмотрим пример расчета параметров автоколебаний гармоническим методом в САУ, изображенной на рис.3.13.

Частотная характеристика линейной части имеет вид

(3.28)

Амплитудная характеристика гистерезисного двухпозиционного реле имеет вид

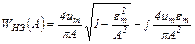(3.29)

Уравнение (3.26) может быть записано в виде

После подстановок в него выражений (3.28) и (3.29) получим

(3.30)

Уравнение (3.30) распадается на два уравнения

(3.31)

Из первого уравнения системы (3.31) находим амплитуду автоколебаний

А_АК=ε_т ,

а из второго – частоту и период автоколебаний

Точные параметры автоколебания, определенные в теме 3.5, имеет значения

Погрешность в определении периода автоколебаний Т_АК гармоническим методом объясняется тем, что этот метод является приближенным. Действительный график автоколебательного процесса имеет треугольную форму (рис.3.3), который существенно отличается от синусоидального графика.

Вопросы и задания

1. Поясните графическое определение параметров автоколебаний гармоническим методом.

2. Поясните аналитическое определение параметров автоколебаний гармоническим методом.

 

 

3.10. Устойчивость нелинейных САУ

Для нелинейной САУ с невысоким порядком дифференциального уравнения линейной части (не выше 3-го порядка) устойчивость может быть определена прямым методом путем расчета фазовых траекторий. Если в результате расчета получены сходящиеся фазовые траектории, подобные приведенным на рис.3.6а и рис.3.7а, или фазовая траектория является замкнутой, то САУ будет устойчива. Здесь к устойчивым отнесены нелинейные САУ, в которых существуют автоколебания – незатухающие негармонические колебания. Отнесение автоколебательных САУ к устойчивым объясняется тем, что для многих нелинейных САУ такой режим является нормой.