Вопросы и задания
1. Какие элементы входят в САУ курсом судна и какие их передаточные функции?
2. Зачем элементы рулевого привода дважды охвачены жесткими обратными связями?
3. Как исследовать на устойчивость САУ курсом судна?
4. Как обеспечить устойчивость САУ курсом судна в любых условиях его эксплуатации? Каковы ошибки удержания судна на заданном курсе?
1.22. Сущность процесса синтеза САУ.
Частотный метод синтеза линейных САУ
Синтез САУ представляет собой процедуры определения вида и характеристик корректирующего устройства или регулятора, с помощью которых система с исходным набором звеньев и их характеристик при заданных внешних задающих и возмущающих воздействиях работает с заданным качеством.
Методы синтеза классифицируются по критериям (показателям качества), используемых при синтезе, характеристиками входных сигналов, структурой исходной схемы и алгоритм решения задачи синтеза.
Синтез КУ следящих систем производится частотным методом с использованием ЛАЧХ по обобщенной структурной схеме САУ, приведенной на рис.1.77.
Исходные данные для синтеза:
1. Передаточная функция WН (p) неизменяемой части САУ.
2. Показателями качества (критериями синтеза) являются:
- максимальная ошибка регулирования εт в следящем режиме;
- показатель колебательности М.
Ошибка регулирования εт является прямым показателем качества, а показатель колебательности М – косвенным. Зная М, можно по рис.1.47 найти перерегулирование σ.
3. Характеристиками входного сигнала являются: максимальные скорость 
и ускорение 
его изменения.
Этапы синтеза:
1. Строится ЛАЧХ неизменяемой части системы LН, например, вида, изображенного на рис.1.78.
2. Строится желаемая ЛАЧХ LЖ синтезированной САУ (рис.23.2). Желаемая ЛАЧХ LЖ состоит из четырех участков: низкочастотного (НЧ), среднечастотного (СЧ), высокочастотного (ВЧ) и сверхвысокочастотного (СВЧ).
Построение НЧ участка. Форма LЖ на НЧ участке определяется требованием точности εт с учетом параметров и входного сигнала. Участок состоит из двух отрезков, исходящих из контрольной точки К с координатами ωК и LK, с наклонами –1 и –2. Сначала определяется базовая частота
.)
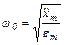Затем рассчитываются координаты контрольной точки К:
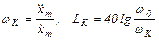
Ниже отмеченных прямых находится запретная область. Если LH проходит через запретную область, то заданная точность εт в следящем режиме не будет обеспечена и, поэтому, необходимо вводить корректирующее устройство КУ.
Построение СЧ участка. Форма LЖ на CЧ участке определяется требованием обеспечения заданного показателя колебательности М с учетом параметров и входного сигнала. СЧ участок состоит из одного отрезка с наклоном –1. Границы отрезка по оси частот определяются двумя частотами сопряжения wt и 
которые определяются через постоянные времени
В диапазоне частот СЧ участка проверяется то, чтобы резонансный выброс ЛАЧХ LНd не заходил в запретную область.
Построение ВЧ участка. ВЧ участок влияет только на показатель колебательности М, располагается в диапазоне частот от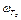 
до граничной wГР, равной wГР»40w0, и должен состоять из одного отрезка с наклоном -2. Однако с целью получения наиболее простой схемы корректирующего устройства КУ допускается введение на ВЧ участке дополнительных изломов с последующим пересчетом частоты 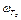. Упрощение схемы КУ достигается при условии, что в диапазоне частот от 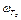до wГР желаемая ЛАЧХ LЖ будет повторять все изломы ЛАЧХ LНd. В нашем примере нужно повторить излом на частоте w2 с одновременным пересчетом постоянной времени и частоты сопряжения правого конца СЧ участка:
Построение СВЧ участка. СВЧ участок располагается правее частоты wГР. Он не влияет ни на один показатель качества и его форма определяется только требованиями получения наиболее простой схемы корректирующего устройства КУ. Упрощение схемы КУ достигается при условии, что желаемая ЛАЧХ LЖ будет повторять все наклоны ЛАЧХ LН.
3. По ЛАЧХ LЖ восстанавливается желаемая передаточная функция САУ. Так для приведенной на рис.23.2 ЛАЧХ LЖ передаточная функция будет
При известной передаточной функции WH (р) неизменяемой части передаточная функция КУ находится из выражения
Вопросы и задания
1. Сформулируйте постановку задачи и исходные данные для синтеза следящей САУ.
2. Какие исходные данные определяют форму НЧ участка желаемой ЛАЧХ? Что такое "запретная область"?
3. Какие исходные данные определяют форму СЧ участка желаемой ЛАЧХ?
4. Как строятся ВЧ и СВЧ участки желаемой ЛАЧ?
2. САУ СО СЛУЧАЙНЫМИ СИГНАЛАМИ
2.1. Типы случайных процессов и их характеристики
Многие судовые системы работают в условиях действия на них случайных сигналов, например, сил ветра и волн, действующих на корпус судна, мощности электрической нагрузки электростанции при включении и выключении электроприемников в случайные моменты времени.
Случайным процессом называется функция времени x (t), которая в момент времени t принимает случайное значение. Если многократно в течение интервала времени Т вести наблюдение (вести запись) за случайным сигналом х, то каждый раз будет получена реализация случайного процесса, не совпадающая со всеми предшествующими реализациями (рис.2.1). Поэтому ни о каком строгом математическом описании графика случайного процесса не может быть речи. Реально можно определить и затем использовать в расчетах САУ некоторые обобщенные (интегральные) характеристики случайных процессов.
Числовые характеристики случайных процессов
Для решения задач ТАУ достаточным является использование следующих характеристик случайных процессов: функции распределения, плотности вероятности, математическое ожидание, корреляционные функции.
Функцией распределения
называется вероятность того, что в момент времени t значение x (t) не превысит заданного хЗАД.
Плотностью вероятности называется частная производная по х от функции распределения
Плотности вероятности подчиняется формуле
,
которая отражает очевидный факт, что случайная величина x (t) в любой момент времени из бесконечного интервала -∞<t<∞ примет какое-то конкретно значение.
Математическое ожидание процесса x(t) в заданный момент времени t
(2.1)
является средним значением по множеству реализаций случайного процесса x (t).
На рис.2.1 показаны значения тх (t1) и тх (t2) из множества реализаций { x1 (t), x2 (t) ,…,xn (t)}, которые при ограниченном числе п реализаций находятся по формуле усреднения
(2.2)
Вычисления математического ожидания по точной формуле (2.1) или по приближенной (2.2) неудобны тем, что для них требуется информация о бесконечно большом числе реализаций случайного процесса. Из-за реальной ограниченности числа реализаций п в формуле (2.2) применен знак приближенного равенства 
.
Вычисление математического ожидания может быть упрощено для случайных процессов, обладающих свойствами стационарности и эргодичности.
Случайный процесс называется стационарным, если среднее значение по множеству реализаций на любом временном интервале длительностью Т (рис.2.1) является одним и тем же постоянным числом
тх (t) =idem при 
,
где t0 – любой момент начальный момент времени t интервала Т.
Стационарный случайный процесс называется эргодическим, если среднее значение по множеству реализаций равно среднему значению по времени
На основании свойств стационарности и эргодичности можно вычислить математическое ожидание тх на основе только одной достаточно продолжительной реализации случайного процесса, например, процесса х2 (t) (рис.2.1).
Свойства стационарности и эргодичности не являются очевидными и на практике строго не выполняются. Эти свойства можно принимать в качестве гипотезы, но с обязательной последующей проверкой в эксперименте. Такие способы проверки существуют, которыми устанавливается также уровень достоверности гипотезы.
Дисперсия Dx или среднеквадратичное значение центрированного случайного процесса x(t):
, (2.3)
где 
- центрированный случайный процесс.
Корреляционные функции:
Корреляционные функции характеризуют взаимозависимость (тесноту связей) между значениями случайных сигналов, отстоящих друг от друга по времени на величину τ. В зависимости от вида случайных сигналов, между которыми устанавливается теснота связей, корреляционные функции подразделяются на автокорреляционные и взаимные корреляционные.
а). Автокорреляционная функция
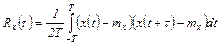(2.4)
Численное значение автокорреляционной функции характеризует тесноту связей между парами значений случайного сигнала x (t), которые отстоят друг от друга по времени на величину τ. Чем больше значение Rx (τ), тем сильнее значение x (t+τ) зависит от значения x x (t). При Rx (τ) =0 значение x (t+τ) не зависит от значения x (t).
Значение автокорреляционной функции Rx (τ) при τ=0 совпадает со значением дисперсии
(2.5)
б). Взаимная корреляционная функция
(2.6)
Численное значение взаимной корреляционной функции характеризует тесноту связей между парами значений случайных сигналов x (t) и у (t), которые отстоят друг от друга по времени на величину τ. Чем больше значение Rxу (τ), тем сильнее значение у (t+τ) зависит от значения x (t). При Rxу (τ) =0 значение у (t+τ) не зависит от значения x (t).
Вопросы и задания
1. Дайте определение случайному процессу и функции распределения.
2. Дайте определения математическому ожиданию для случайных процессов общего вида, а также для стационарных и эргодических.
3. Дайте определение дисперсии и корреляционной функции.
2.2. Прохождение стационарного случайного сигнала
через линейное звено
Выходной сигнал линейного, на вход которого поступает сигнал со случайными характеристиками, является также случайным. Необходимо уметь рассчитывать характеристики случайного выходного сигнала по передаточной функции линейного звена и характеристики случайного выходного сигнала. Для решения указанной задачи потребуется еще одна характеристика случайного процесса – спектральная плотность Sx (ω).
Спектральной плотностью случайного процесса называется Фурье-преобразование от автокорреляционной функции
(2.7)
Существует обратное Фурье-преобразование
(2.8)
Исследования свойств спектральной плотности Sx (ω) показывает, что она является всегда четной функцией Sx (ω) = Sx (- ω), т.е. ее значение не зависит от знака частоты ω. Это свойство четности позволяет видоизменить формулу (2.8)
Это определение Rx (τ) и свойство (2.5) даёт следующую формулу определения дисперсии
, (2.9)
которая является центральной в расчетах прохождения случайного сигнала через линейное звено.
У спектральной плотности Sx (ω), введенной чисто формально преобразованием (2.7), имеется четкий физический смысл, а именно, Sx (ω) является энергетической характеристикой случайного процесса. Любой случайный процесс теоретически можно представить в виде суммы гармонических составляющих в диапазоне частот ω=0…∞. Вводится определение величины энергии случайного процесса в окрестности dω гармонической составляющей с частотой ω
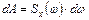
С этим определением Sx (ω) полная энергия случайного процесса выразится как
(2.10)
Сопоставляя (2.10) с (2.9), можно сделать заключение, что дисперсия Dx также является энергетической характеристикой случайного процесса x (t). Для обоснования такой трактовки дисперсии рассмотрим электрическую цепь (рис.2.2), в которой ток i в резисторе R создаёт источник шумов с э.д.с. еШ. Э.д.с. еШ изменяется случайным образом и ее происхождение связано с тепловым движением электрических зарядов в элементах, входящих в электрическую цепь, таких как соединительные проводники, резисторы и т.д.
Мощность шумов рШ, выделяемая в резисторе R, равна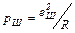 
, а средняя мощность источника шумов за время 2Т составит
(2.11)
При математическом ожидании те сигнала еШ равном нулю его дисперсия согласно (2.3) будет следующей
(2.12)
Из сопоставления (2.11) и (2.12) следует, что дисперсия De сигнала еШ прямо пропорциональная средней мощности РСР источника шумов. С учетом формулы (2.9) получаем пропорцию
РСР ~ 
,
которой и доказывается энергетический смыл спектральной плотности.
Рассмотрим пример расчета автокорреляционной функции и спектральной плотности для гармонического одночастотного сигнала х(t) со случайной фазой α (рис.2.3)
Среднее значение данного сигнала нулевое: тх=0. Согласно (2.4) автокорреляционная функция равна
(2.13)
Полученное выражение (2.7) не зависит от случайной величины α, а предсказуемость значения х (t) от через время τ зависит от величины этого времени. Так через время τ равное полупериоду 
гармонического сигнала, корреляционная связь максимальна и последующее за x (t) значение x (t+τ) абсолютно предсказуемо, а при временном сдвиге 
, где п – целое число, последующее за x (t) значение x (t+τ) абсолютно непредсказуемо.
Спектральная плотность согласно (2.7) равна
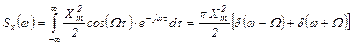(2.14)
Полученное выражение (2.14) не зависит от случайной величины α, а мощность случайного сигнала x (t) переносится целиком на частотах ±Ω.
Графики x (t), Rx (τ) и Sx (ω) для рассмотренного примера приведены на рис.2.3.
Теперь можно решать задачу определения характеристик Sy (ω), Ry (τ } и Dy выходного случайного сигнала при известных характеристиках Sy (ω), Ry (τ } и Dх входного сигнала (рис.2.4).
При известной передаточной функции W (p) линейного звена для него может быть определена функция веса k (t). Случайный сигнал y (t) может быть найден по интегралу свертки
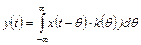
Вычисления по (2.4) автокорреляционной функции Rх (τ }, затем вычисления по (2.7) спектральной плотности дают следующий результат
(2.15)
где А (ω) – АЧХ линейного звена.
Дисперсия случайного сигнала определяется согласно (2.9) формулой
Вопросы и задания
1. Дайте определение спектральной плотности. Какой ее физический смысл?
2. Как через спектральную плотность определить дисперсию?
3. Как определить спектральную плотность и дисперсию выходного сигнала линейного звена при известной спектральной плотности входного сигнала?
2.3. Расчет ошибок регулирования в линейной САУ
при воздействии на нее полезного сигнала с помехой
Рассмотрим замкнутую САУ (рис.2.5), отрабатывающей сигнал задания х (t), и на которую действует сигнал помехи g (t), приложенный к входу объекта управления. В ошибке регулирования помимо регулярной составляющей, зависящей от входного сигнала х (t), присутствует случайная составляющая, зависящая от случайного сигнала g (t). Считаем известными передаточные функции регулятора WP (p) и объекта управления WОУ (p).
Рассчитаем среднеквадратичную ошибку регулирования
В соответствии с (2.12) подкоренное выражение является дисперсией, а в соответствии с (2.9) дисперсия вычисляется через спектральную плотность. Поэтому можно записать
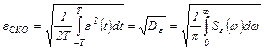(2.16)
Результат (2.16) показывает, что для расчета среднеквадратичной ошибки регулирования εСКО необходимо иметь выражение спектральной плотности Sε (ω) сигнала ошибки ε (t).
По структурной схеме рассчитываем изображение ошибки регулирования ε (р):
откуда
, (2.17)
где WУ (p) и WB (p) - передаточные функции САУ, соответственно, по управлению и возмущению.
Считая сигналы х (t)и g (t) некоррелированными между собой (это значит, что мгновенные значения сигнала х (t) не зависят от сигнала g (t) и наоборот), в соответствии с (2.15) спектральная плотность сигнала ошибки ε (t) будет равна
(2.18)
Формула среднеквадратичной ошибки будет иметь вид
(2.19)
Аналитические выражения АЧХ АУ (ω) и АВ (ω), входящие в выражение (2.19), выводятся из заданных передаточных функций регулятора WP (p) и объекта управления WОУ (p) с учетом определений WУ (p) и WВ (p), отмеченных в (2.17). Аналитические выражения спектральных плотностей Sх (ω) и Sg (ω) определяют либо аналитически (для сигнала х (t) задания), либо статистической обработкой реально наблюдаемых в эксперименте сигналов (для сигнала g (t) помехи). Некоррелированность сигналов х (t) и g (t) также должна быть доказана расчетом. Если все же сигналы х (t) и g (t) окажутся коррелированны с большой степенью связи между ними, то ошибку εСКО следует вычислять по выражению, расширенному в сравнении с (2.19). В расширенное выражение входят дополнительные слагаемые, которые содержат взаимные спектральные плотности, вычисленные через взаимные корреляционные функции (2.13) по формуле
Вопросы и задания
1. Как в САУ, находящейся под действием сигналов задания и помех, найти операторное изображение сигнала ошибки?
2. Как в САУ, находящейся под действием сигналов задания и помех, найти спектральную плотность сигнала ошибки?
3. Как в САУ, находящейся под действием сигналов задания и помех, найти среднеквадратичное значение сигнала ошибки?
2.4. Пример судовой САУ, отрабатывающей
полезный сигнал с помехой
Рассмотрим САУ курсом судна (рис.2.6), состоящей из судна с передаточной функцией WС (p) и авторулевого с передаточной функцией WАР (p). Входным сигналом является сигнал задания х (t) курса судна, а выходным – сигнал у (t) фактического курса. На корпус судна действуют силы ветра и волн, которые обозначены сигналом помехи g (t).
Передаточные функции авторулевого и судна имеют вид
Сигнал задания курса х (t) принимаем постоянным: х (t)= X=const. Для него спектральная плотность имеет вид
Определенная экспериментально спектральная плотность сигнала помехи, вызванная действием волн на корпус судна, имеет вид
В соответствии с (2.17) по структурной схеме на рис.2.6 имеем изображение ошибки регулирования
Спектральная плотность ошибки регулирования согласно (2.18) имеет вид
Квадрат значения εСКО среднеквадратичной ошибки регулирования согласно (2.19) равен
(2.20)
Подинтегральное выражение в формуле (2.20) среднеквадратичной ошибки представляет собой дробь, в числителе и знаменателе которой содержатся многочлены по четным степеням переменной ω. Стандартный вид этой дроби позволил вычислить интеграл в общем виде и результаты таких вычислений сведены в таблицу, которую можно найти в задачниках и справочниках по расчетам САУ.
Эффективным средством уменьшения среднеквадратичной ошибки εСКО регулирования является применение в авторулевом Д -регулятора. За счет изменения постоянной времени ТД возможно уменьшение ошибки εСКО в заданных условиях плавания и загрузки судна. Для определения оптимального значения ТД.ОПТ, при котором εСКО становится минимальной, необходимо при вычислении выражения (2.20) параметру ТД не придавать числовое значение, а оставить его буквой. Тогда выражение квадрата ошибки будет получено в виде функциональной зависимости
Условием выбора оптимального значения ТД.ОПТ является равенство нулю производной от 
:
Настройкой ТД.ОПТ достигаем минимальной среднеквадратичной ошибки регулирования.
Вопросы и задания
1. Какой вид имеют сигналы задания и помехи в САУ курсом судна и каковы выражения их спектральных плотностей?
2. Как определяется среднеквадратичное значение ошибки судна на курсе?
