5. Поясните свойства неооднозначности оригиналов и z-изображений импульсных сигналов и как эту неоднозначность свести к минимуму?
4.4. Дискретные передаточные функции звеньев
Пусть на вход непрерывной части с передаточной функцией WНЧ(р) поступают импульсы xИ (t), сформированные амплитудно-импульсным модулятором АИМ из непрерывного сигнала x (t) (рис.4.12). Выходной сигнал у (t) непрерывной части является суммой реакций на отдельные импульсы xИ (t), поступившие на ее вход.
Для реализации возможности расчета с использованием z -изображений реакции непрерывной части на поступающие на её вход прямоугольные импульсы, перейдем к эквивалентной импульсной САУ, изображенной на рис.4.13.
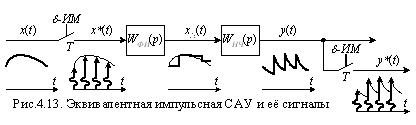
Входной непрерывный сигнал x (t) преобразуется дельта-импульсным модулятором δ-ИМ в импульсную функцию x* (t). Сигналы x* (t) импульсной функции поступают на формирователь импульсов, являющийся линейным звеном с некоторой передаточной функцией WФИ (р), который импульсы x* (t) превращает в реальные прямоугольные импульсы xИ (t). На выходе непрерывной части с передаточной функцией WНЧ (р) образуются действительный сигнал у (t). Установим на линии сигнала у (t) дельта-импульсный модулятор δ-ИМ, работающий с периодом Т синхронно с модулятором сигнала x (t). В результате модуляции будут получена импульсная функция у* (t). У этой импульсной функции площади отдельных импульсов будут равны значениям выходного сигнала у (t) в дискретные моменты времени.
Определим передаточную функцию WФИ (р) формирователя импульсов исходя из заданных сигналов на его входе и выходе (рис.4.14). Выходной единичный импульс 1И (t) ФИ может быть заменен разностью дух единичных скачков 1 (t) и 1 (t-Т), которые сдвинуты относительно друг друга на период Т, т.е. 1И (t) =1 (t) -1 (t-Т). Изображения по Лапласу входного и выходного сигналов имеют вид
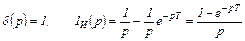
Передаточная функция ФИ определим как
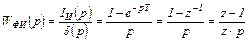
Два последовательно соединенных линейных звена на рис.4.13 заменяем одним звеном, называемым приведенной непрерывной частью, с передаточной функцией
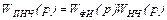
Схема с рис.4.13 превратится в схему, приведенную на рис.4.15.
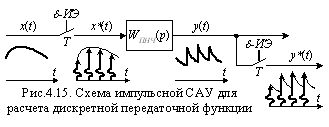
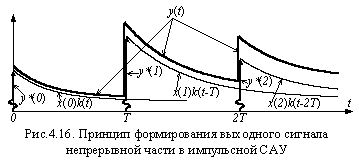
От входной х* (t) и выходной у* (t) импульсных функций существуют соответствующие z -изображения x (z) и y (z). Установим связь между импульсными функциями х* (t) и у* (t) с использованием рис.4.16.
Входной сигнал х* (t) представляет собой (см. (4.3)) сумму δ -импульсов, сдвинутых по оси времени на п тактов и имеющих площадь, равную х (п). Реакцией приведенной непрерывной части на каждый δ -импульс является функция веса k (t-nT), сдвинутая вправо на п тактов и умноженная на площадь входного импульса, которая равна х (п). На рис.4.16 показаны графики х (0) k (t), х (1) k (t-T), х (2) k (t-2T) как реакции приведенной непрерывной части на импульсы х*(0), х*(1),х*(2) входного сигнала х* (t). Суммой графиков х (0) k (t), х (1) k (t-T), х (2) k (t-2T),…. является выходной сигнал у (t). Дельта-импульсный модулятор из сигнала у (t) формирует импульсную функцию у* (t), состоящую из импульсов у* (0), у* (1), у* (2),….
Импульсная функция выходного сигнала у (t) по определению (см. (4.3)) равна
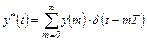(4.9)
Выходной сигнал у (t) согласно рис.4.16 определяется выражением
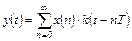(4.10)
Подставляем (4.10) в (4.9)
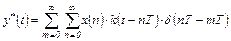(4.11)
Применив к (4.11) преобразование Лапласа и затем, перейдя к z -изображению, получим
(4.12)
Выражение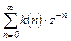 
называется дискретной передаточной функцией (ДПФ) звена
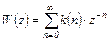(4.13)
Согласно (4.12) определение дискретной передаточной функции такое же, как и в линейной САУ, а именно, есть отношение изображений выходного и входного сигналов звена
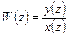(4.14)
Смысл дискретной передаточной функции заключается в том, что она связывает между собой решетчатые функции и, следовательно, амплитуды импульсов на входе и выходе звена. Если известна решетчатая функция x (z) входного сигнала, то с использованием дискретной передаточной функции W (z) можно рассчитать решетчатую у (z) функцию выходного сигнала звена. Результат (4.14) свидетельствует, что импульсные САУ в отношении решетчатых функций или амплитуд импульсов являются линейными САУ.
ДПФ можно вычислить либо по формуле (4.13), либо по более удобной в расчетах формуле
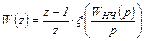, (4.15)
где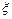 
– символ, указывающий на операцию перехода от изображения по Лапласу к z -изображению.
Числовой пример
Пусть передаточная функция звена непрерывной части имеет вид
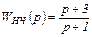
Найти ДПФ, если период следования импульсов Т=0,1 с.
Решение.
Согласно (4.15)
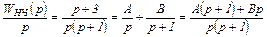(4.16)
Для определения коэффициентов А и В составляем и решаем систему уравнений
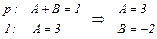
Подставляем А и В в (4.16), затем (4.16) – в (4.15) и, используя табл.4.1, находим
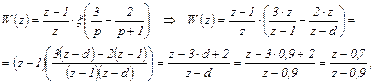(4.17)
где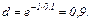 
Вопросы и задания
1. Зачем в исходную импульсную систему введены δ-ИМ, с помощью которых образованы сигналы импульсных функций от входного и выходного сигналов?
2. Поясните вывод передаточной функции формирователя импульсов.
3. Поясните принцип формирования выходного сигнала непрерывной части в импульсной САУ.
4. Что является дискретной передаточной функцией и как ее можно вычислить при заданной передаточной функции непрерывной части?
5. Поясните вычисления дискретной передаточной функции, приведенные в примере.
4.5. Дискретные передаточные функции
разомкнутых и замкнутых импульсных САУ
Звенья импульсных САУ имеют ДПФ, как и линейные звенья, и могут соединяться между собой произвольным образом, образуя структурную схему импульсной САУ. Однако подобия между структурными схемами линейных и импульсных САУ, в общем случае не существует в том смысле, что нельзя линейные звенья структурной схемы САУ просто заменить один в один звеньями импульсной САУ, оставив нетронутыми линии связи между ними. Объяснению этому то, что линейное звено с передаточной функцией WНЧ (р) превращается в звено импульсной САУ с ДПФ W (z) только при наличии двух модуляторов - на входе и выходе этих звеньев (рис.4.13).
Рассмотрим типовые соединения звеньев импульсных САУ.
На рис.4.17а приведено последовательное соединение двух звеньев, в линии связи между которыми установлен модулятор, который выходной сигнал v (t) 1-го звена преобразует в АИМ-сигнал vИ (t), являющийся входным для 2-го звена. Модуляторы условно показаны ключами, замыкающимися с периодом Т. Для такого соединения можно каждое линейное звено заменить на звено импульсной САУ с ДП
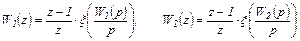
Эквивалентная ДПФ такого соединения будет такой же, как и в линейных САУ
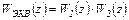(4.18)
На рис.4.17б приведено последовательное соединение двух звеньев, которые между собой связаны непрерывным сигналом v (t). Условие перехода к ДПФ по формулам нарушено. Эквивалентная ДПФ должна рассчитываться по формуле
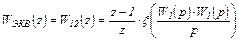(4.19)
Можно доказать, что в этом случае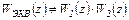 
.
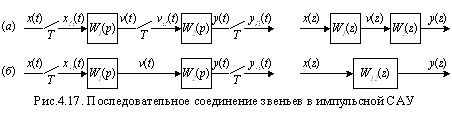
Для параллельного соединения (рис.4.18) эквивалентная ДПФ рассчитывается по формуле
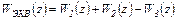(4.20)
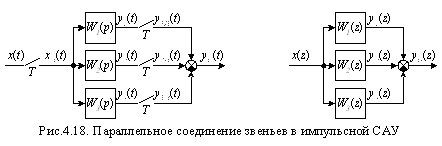
Для соединения с отрицательной обратной связью (рис.4.19) эквивалентная ДПФ замкнутой САУ рассчитывается по формуле
(4.21)
Два ключа на входе элемента сравнения преобразуют непрерывные сигналы х (t) и y (t) в импульсы хИ (t) и yИ (t), которые затем вычитаются, формируя импульс εИ (t) сигнала ошибки. Но тот же импульс εИ (t) может быть получен таким образом, когда сначала вычитаются непрерывные сигналы х (t) и y (t), образуя этим непрерывный сигнал ε (t), а затем он модулятором превращается в импульс εИ (t).
Далее будем использовать только структурные схемы линейных САУ с ДПФ, полагая, что звенья этой схемы определены корректно.
Числовой пример
Пусть ДПФ разомкнутой САУ имеет вид (4.17)
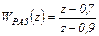
ДПФ замкнутой САУ в соответствии с формулой (4.21) будет следующей
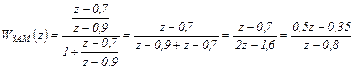(4.22)
Вопросы и задания
1. Какова эквивалентная ДПФ последовательно соединенных звеньев? Как на расчет эквивалентной ДПФ влияет вид сигнала, которым связаны звенья последовательной цепи?
2. Какова эквивалентная ДПФ параллельно соединенных звеньев?
3. Какова эквивалентная ДПФ соединения звеньев с обратной связью?
4. Поясните вычисления дискретной передаточной функции, приведенные в примере.
4.6. Методы расчета переходных процессов
в импульсных САУ
По определению (см. тема 2) переходным процессом называется реакция САУ на единичный скачок.
Если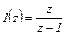 
- z -изображение входного сигнала САУ и WЗАМ (z) – ДПФ импульсной САУ, то в соответствии с определением ДПФ (41.9), z -изображение переходного процесса будет иметь вид
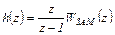(4.23)
Далее методы расчета изучим на числовых примерах.
При WЗАМ (z) вида (4.22) z -изображение переходного процесса будет следующим
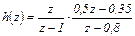(4.24)
Расчет переходного процесса в импульсной САУ состоит в определении амплитуд импульсов выходного сигнала h (z) или, что эквивалентно, - расчет решетчатой функции h (n). Существуют два метода расчета:
1) метод разложения h (z) в ряд по степеням z-n;
2) табличный метод.
1. Метод разложения (распаковки) h (z) в ряд по степеням z-n
Преобразуем (43.2) к стандартному виду
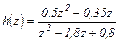
Выполним деление многочлена 0,5z2-0,35z на многочлен z2-1,8z+0,8
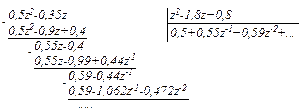
Результатом деления является ряд
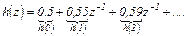, (4.25)
коэффициентами которого при степенях z-n являются значения решетчатой функции h (n) переходного процесса (см. (4.8)).
Заполним табл.4.2 и построим график переходного процесса (рис.4.20).
Таблица 4.2
Значения решетчатой функции переходного процесса
| Номер импульса п | ∞ | ||||||||||
| h (n) из ряда (4.25) | 0,5 | 0,55 | 0,59 | ||||||||
| h (n) из формулы (4.28) | 0,5 | 0,55 | 0,59 | 0,622 | 0,648 | 0,668 | 0,684 | 0,698 | 0,708 | 0,716 | 0,75 |
Достоинством метода является непосредственное определение решетчатой функции h (п) из выражения h (z) при минимуме предварительных его преобразований h (z).
Недостатком метода является то, что при заранее неизвестном установившемся значении решетчатой функции h (п) является неопределенным число необходимых делений двух многочленов.
2. Табличный метод
Преобразуем (4.24) к сумме табличных z -выражений (табл.4.1)
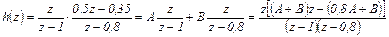(4.26)
Для определения коэффициентов А и В составляем и решаем систему уравнений
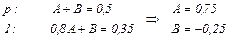
Подставляем А и В в (4.26), и, используя табл.4.1, находим оригинал h (t)
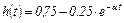, (4.27)
где α должно быть таким, чтобы было (см. табл.4.1)
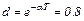
В выражении (4.27) нужно брать дискретное время, значения которого совпадают с периодом Т следования импульсов:
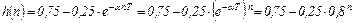(4.28)
Вычисления h (п) по формуле (4.28) даёт те же значения решетчатой функции, которые были определены 1-м методом (табл.4.2).
Имея формулу выражения переходного процесса, можно определить установившееся значение переходного процесса и его длительность в импульсах.
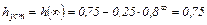
Для расчета длительности переходного процесса преобразуем (4.28)
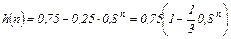
Длительность переходного процесс в импульсах находим из уравнения
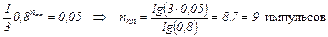
Вопросы и задания
1. Как рассчитать z-изображение переходного процесса?
2. Поясните метод расчета переходного процесса разложением в ряд.
3. Поясните табличный метод расчета переходного процесса.
4. Как рассчитать установившееся значение и продолжительность переходного процесса?
4.7. Устойчивость импульсных САУ
Устойчивость импульсных САУ можно оценивать прямым методом и с использованием критериев.
Прямой метод оценки устойчивости заключается в расчете и построении графика переходного процесса: для устойчивой САУ значение h (∞) должно быть конечной величиной, которое называется установившемся значением hуст переходного процесса. Однако расчет и построение графика являются достаточно трудоемкими операциями.
Несколько проще суждение об устойчивости может быть вынесено на основе анализа корней zi характеристического уравнения ДПФ (характеристическое уравнение составляется путем приравнивания к нулю знаменателя ДПФ замкнутой САУ). Эти корни определяют значения параметра di (см. табл.40.1), равного, соответственно, для устойчивого экспоненциального и затухающего колебательного процессов
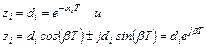(4.29)
Значение αi затем входит в показатель экспоненты выражения оригинала h (t). САУ будет устойчива, если значения αi для всех корней zi будет положительным, а, согласно (4.29), все корни zi характеристического уравнения по модулю меньше 1: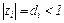 
.
Прямые методы имеют тот недостаток, что позволяют судить об устойчивости для САУ с невысоким порядком характеристического многочлена ДПФ (не выше 2-го порядка). В общем случае задача оценки устойчивости проще решается с помощью критериев устойчивости.
После соответствующих преобразований выражения ДПФ оценка устойчивости может быть произведена критериями Гурвица, Михайлова, Найквиста. Рассмотрим применение критерия Гурвица, который базируется на анализе характеристического многочлена D (z) ДПФ замкнутой импульсной САУ. Предварительно в D (z) производится следующая замена
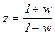(4.30)
Данная замена обладает тем свойством, что при | z | <1 переменная w имеет отрицательную действительную часть (Re (w)< 0), что доказывается следующими преобразованиями:
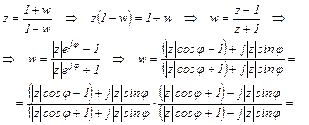
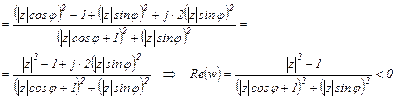
Следовательно, выражение D (w) должно быть проверено на отрицательность действительных частей его корней. Это как устанавливается с использованием критериев устойчивости Гурвица, Михайлова, Найквиста и др.
Примеры:
1. Исследуем с использованием критерия Гурвица устойчивость импульсной САУ, если ее ДПФ имеет 1-й порядок
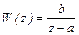
Решение.
В характеристическом многочлене D (z) =z-a выполняем замену (4.30):
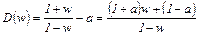
В соответствии с критерием Гурвица САУ 1-го порядка устойчива, если все коэффициенты характеристического многочлена D (w) положительны
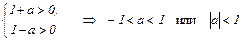
2. Исследуем на устойчивость импульсную САУ, если ее ДПФ имеет 2-й порядок
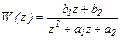
Решение.
В характеристическом многочлене D(z)=z-a выполняем замену (44.2)
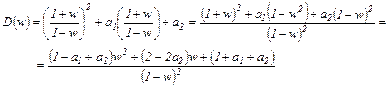
В соответствии с критерием Гурвица САУ 2-го порядка устойчива, если все коэффициенты числителя многочлена D (w) положительны
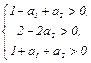(4.31)
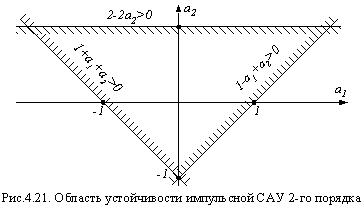
Графическое решение системы неравенств (4.31) показано на рис.4.21. Область устойчивости отмечена штриховкой.
Вопросы и задания
1. При каких значениях корней характеристического уравнения ДПФ импульсная САУ будет устойчивой?
2. Почему неприменимы критерии устойчивости Гурвица, Михайлова и Найквиста к характеристическому многочлену D ( z ), а к характеристическому многочлену D ( w ) применимы?
3. При каких значениях коэффициентов характеристического многочлена ДПФ 1-го порядка САУ устойчива?
4. При каких значениях коэффициентов характеристического многочлена ДПФ 2-го порядка САУ устойчива?
4.8. Синтез корректирующих устройств
и регуляторов импульсных САУ
Одним из требований к САУ может быть формирование заданного графика решетчатой функции переходного процесса. Так в рассчитанный в теме 4.6 переходный процесс при заданной передаточной функции непрерывной части WИЧ (р) имеет следующие недостатки:
1) установившаяся ошибка регулирования составляет 25%, что, безусловно, очень много;
2) длительность переходного процесса составляет 9 тактов, что также является слишком большой величиной.
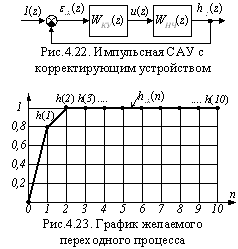
В импульсных САУ достаточно прост синтез корректирующего устройства, с которым в САУ устанавливается желаемый переходный процесс. Процесс синтеза, для большей его наглядности, рассмотрим на числовом примере. Структурная схема синтезированной САУ имеет стандартный вид (рис.4.22). В качестве корректирующего устройства выберем микропроцессорное. Это устройство работает с амплитудно-модулированными импульсными на входе и выходе (см. рис.4.5), поэтому условия для использования формулы (4.18) выполняются.
Задаемся графиком желаемого переходного процесса hЖ (п) (рис.4.23), у которого ошибка регулирования составляет 0%, а длительность переходного процесса составляет 2 такта.
Значения решетчатой функции hЖ (п) графика желаемого переходного процесса заносим в табл.4.3. Далее вычисляем значения решетчатой функции εЖ (п) =1 (п) -hЖ (п) (формула следует из рис.4.22) графика желаемой ошибки регулирования и также заносим в табл.4.3.
Таблица 4.3
Данные для желаемых графиков hЖ(п) и εЖ(п)
| Номер п импульса | … ∞ | ||||
| Значения желаемого графика hЖ (п) | 0,8 | ||||
| Значения желаемого графика εЖ (п) | 0,2 |
Значение εЖ (п) содержат конечное число ненулевых элементов и бесконечное – нулевых. Используя представление z -изображения в виде ряда (см. (4.8)), по данным табл.4.3 запишем для εЖ (п) конечный ряд
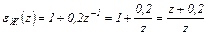
Запишем, используя hЖ (z) =1 (z) -εЖ (z), z -изображение для сигнала hЖ (z):
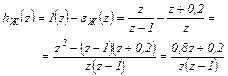
Используя определение ДПФ (см. (4.14)), определяем желаемую ДПФ разомкнутой САУ
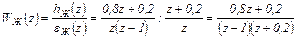
Так как согласно структурной схемы, изображенной на рис.45.1,
,
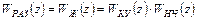то ДПФ корректирующего устройства будет иметь вид
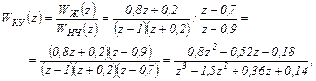(4.32)
где WНЧ (z) взято равным выражению (4.17) ДПФ непрерывной части разомкнутой САУ.
Если график желаемого переходного процесса hЖ (п) будет иметь конечное число ненулевых значений и бесконечное – нулевых (рис.4.24), то сначала составляется выражение hЖ (z) в виде конечного ряда, а затем вычисляется εЖ (z) =1 (z) -hЖ (z).
Вопросы и задания
1. Как на основании желаемого графика переходного процесса составить z-изображения выходного сигнала САУ и сигнала ошибки?
2. Как рассчитать ДПФ корректирующего устройства импульсной САУ, обеспечивающей желаемый график переходного процесса?
4.9. Реализация микропроцессорных корректирующих
устройств по заданным дискретным передаточным функциям
Пусть z -изображение для сигнала х (z) имеет вид ряда
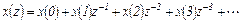
Образуем смещенное на т тактов вправо z -изображение, умноженное на ат,
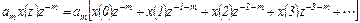
Ограничимся, для определенности, исходным и смещенными на 1 и 2 такта изображениями, и построим их графики x (n), a1x (n) z-1 и a2x (n) z-2 (рис.4.25).
Суммой исходного и смещенных z -изображений является выражение
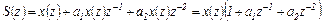(4.33)
Представим z -изображение суммы S(z) в виде ряда
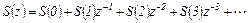
Пользуясь построениями, приведенными на рис.4.25, рассчитаем всего одно значение решетчатой функции суммы S (z)
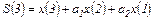
или, обобщая для произвольного п -го такта, получим
,
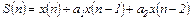причем значения решетчатой функции для тактов с отрицательными номерами (х (-1), х (-2) и т.д.) принимаются равными нулю.
Из сопоставления выражений z -изображения суммы S (z) (4.33) и значения решетчатой функции суммы S (п) для любого п- го такта (4.34) видно, что:
1) в выражение суммы (4.34) входят только значения решетчатой функции исходного сигнала (х (п), х (п-1), х (п-2)и т.д.), взятые с такими номерами импульсов, которые смещены влево (назад) относительно п -го импульса на количество тактов, равное показателю степени у оператора z в выражении S (z) (4.33);
