Максимальная погрешность замен (1.36) достигается на частоте сопряжения и составляет 6 дБ.
Пусть ωс.min минимальная частота сопряжения, определенная для передаточной функции W (p), представленной в виде (1.31). Тогда в соответствии с (1.35) и (1.38) для диапазона частот ω<ωс.min все скобки двучлены и трехчлены можно принять равными 1 и приближенные передаточная функция, АЧХ и ЛАЧХ будут иметь вид:
(1.38)
где V=lg ω.
В осях V – L первый участок ЛАЧХ LI при ω<ωс.min, представляет собой прямую линию, проходящую через точку 20 lg K с коэффициентом наклона –20 ν дБ/дек. Так как наклоны всех участков ЛАЧХ будут иметь наклоны кратные числу 20, то наклон будем обозначать просто как –ν.
Предположим, что частота сопряжения ωс.min порождена скобкой двучленом 
, находящейся в числителе передаточной функции (т.е. 
). Тогда при ω≥ωс.min согласно (1.34) приближенные передаточная функция, АЧХ и ЛАЧХ будут иметь вид:
(1.39)
В осях V – L второй участок ЛАЧХ LII при ω≥ωс.min, представляет собой прямую линию, проходящую с наклоном – (ν-1) через конечную точку первого участка на частоте ωс.min.
Аналогично можно построить 3-й, 4-й и все последующие участки ЛАЧХ, которые всегда будут прямыми линями с наклонами кратными числу 20.
Обобщением изложенного является следующий алгоритм построения ЛАЧХ:
1). По выражению (1.31) находим все частоты сопряжения ωс, упорядочиваем их по возрастанию от значения ωс.min до значения ωс.mах.
2). Составляем выражение передаточной функции WI (p) первого для первого участка ЛАЧХ. Задаемся любой частотой из диапазона ωI<ωс.min и вычисляем ординату LI (ωI) первого участка ЛАЧХ. Через точку с координатами ωI и LI (ωI) проводим прямую линию с наклоном –ν до частоты сопряжения ωс.min.
3). Все последующие отрезки ЛАЧХ строим по следующим двум правилам (без вычислений):
а) при переходе частоты сопряжения, порожденной скобкой двучленом 
, наклон ЛАЧХ изменяется на единицу, а порожденной скобкой трехчленом 
- наклон изменяется на два;
б) при переходе частоты сопряжения, порожденной скобкой числителя, наклон ЛАЧХ изменяется в положительную сторону, а порожденной скобкой знаменателя – наклон ЛАЧХ изменяется в отрицательную сторону.
Числовой пример
Построить ЛАЧХ для САУ с передаточной функцией вида
Решение:
1). Приводим W (p) к стандартному виду типа (1.31):
где 
.
2). Рассчитываем частоты сопряжения и логарифм от них
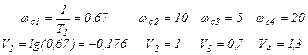(1.40)
3). Подготавливаем плоскость V – L к построению ЛАЧХ (рис.1.9), для чего отмечаем на ней вертикальными пунктирными линиями значения V1, V2, V3 и V4, взятые из (1.40).
4). Составляем выражение передаточной функции WI (p) первого для первого участка ЛАЧХ
Учитывая минимальное значение частоты сопряжения ωс.min=0,67, задаемся частотой ωI=0,1 из диапазона ωI<ωс.min и вычисляем ординату LI (ωI) первого участка ЛАЧХ
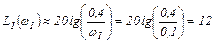дБ.
Через точку с координатами ωI=0,1 и LI (ωI) =12 проводим прямую линию с наклоном –1 (так как ν=1)до частоты сопряжения ωс.min=0,67.
5). Все последующие отрезки ЛАЧХ строим по двум вышеназванным правилам (без вычислений).
Так как частота сопряжения ωс1=0,67, разделяющая I -й и II- й участки ЛАЧХ, порождена скобкой двучленом числителя, то наклон линии II- го участка будет равен 0, что следует из вычислений –1+1=0.
Так как частота сопряжения ωс3=5, разделяющая II -й и III- й участки ЛАЧХ, порождена скобкой трехчленом знаменателя, то наклон линии III- го участка будет равен -2, что следует из вычислений 0-2=-2.
Так как частота сопряжения ωс2=10, разделяющая III -й и IV- й участки ЛАЧХ, порождена скобкой трехчленом числителя, то наклон линии IV- го участка будет равен 0, что следует из вычислений –2+2=0.
Так как частота сопряжения ωс4=20, разделяющая IV -й и V- й участки ЛАЧХ, порождена скобкой двучленом знаменателя, то наклон линии V- го участка будет равен -1, что следует из вычислений 0-1=-1.
ЛАЧХ построена.
Вопросы и задания
1. Как привести передаточную функцию к стандартной форме, пригодной для расчетов ЛАЧХ?
2. Какие замены применяются к выражению АЧХ и какова погрешность таких замен?
3. Как рассчитывается 1-й участок ЛАЧХ и как определяется его положение и наклон?
4. По каким правилам строятся участки ЛАЧХ, следующие за 1-м?
5. Поясните расчеты и построения ЛАЧХ на основе числового примера.
1.5. Типовые позиционные звенья САУ
Звенья САУ могут иметь передаточную функцию с полиномами числителя и знаменателя произвольного порядка
(1.41)
Для полиномов, составляющих числитель и знаменатель выражения передаточной функции (1.41), можно найти корни, которые могут быть только одного из четырех типов: нулевыми р=0, действительными р=-α, комплексными р1,2=-α±jβ и мнимыми р1,2=±jβ. С учетом найденных корней полиномы могут быть представлены в виде произведения выражений, соответственно, типа
(1.42)
Звенья САУ, передаточная функция которых содержит кроме постоянных чисел не более двух выражений типа (1.42) в числителе или знаменателе, называют типовыми звеньями. Всем типовым звеньям даны названия.
Типовые звенья подразделяются на позиционные, интегрирующие и дифференцирующие. Позиционные звенья имеют для установившегося режима статические характеристики вида y=kx, аинтегрирующие и дифференцирующие таких характеристик не имеют.
Виды типовых позиционных звеньев:
1. Безинерционное (пропорциональное) звено имеет передаточную функцию и описывается алгебраическим уравнением, соответственно, вида
W(p)=k, y=kx
Примерами безинерционных звеньев служат рычажная передача (рис.1.10а), потенциометрический датчик перемещения (рис.1.10б).
В этих звеньях выходной сигнал у повторяет без задержки по форме входной сигнал х.
Выражение переходного процесса
y=kx
Частотне характеристики
2. Апериодическое (инерционное) звено 1-го порядка имеет передаточную функцию и описывается уравнением вида
где k, Т - коэффициент передачи и постоянная времени звена.
Примерами этого звена служат интегрирующая RC- цепь (рис.1.11а), 'электродвигатель, обмотки которого разогреваются во время работы (рис.1.11б).
Выполним вывод передаточной функции для RC- цепи. Используя закон Ома, получим
Переходный процесс описывается выражением
где вместо x=1(t), как должно быть для переходного процесса, принято фактическое значение сигнала x, благодаря чему рассчитывается реакция звена на скачок произвольной величины.
График переходного процесса приведён на рис.1.11в. Установившееся значение yуст, равное kx, достигается на бесконечности: t®¥. Время переходного процесса tпп, определяемое по моменту окончательного вхождения графика в 5% зону допуска от ууст, составляет 3T. Звено обладает самовыравниванием. Свойство самовыравнивания состоит в том, что звено самостоятельно без применения дополнительного регулирования приходит к постоянному по величине установившемуся значению.
Частотные характеристики
и их графики, приведенные на рис.1.12.
3. Инерционное звено 2-го порядка имеет передаточную функцию
Особенность звена в том, что его характеристическое уравнение имеет действительные корни.
Примерами этого звена служит RLC -цепь (рис.1.13а) при большом сопротивлении R резистора 
, электропривод, приводящий во вращение нагрузку с большим моментом инерции J (рис.6.4б).
Переходный процесс описывается выражением
где с1 и с2 - постоянные интегрирования.
График переходного процесса (рис.1.14а) имеет точку перегиба. Время переходного процесса tпп можно определить только графически.
Частотные характеристики
и их графики, приведенные на рис.1.15.
4. Колебательное звено имеет передаточную функцию
где T - период свободных (незатухающих) колебаний;
ξ - параметр затухания, принимающий значения 0<ξ<1.
Особенность звена в том, что его характеристическое уравнение имеет комплексно сопряженные корни.
Примерами этого звена служит RLC -цепь (рис.1.13а) при малом сопротивлении R резистора 
, электропривод, приводящий во вращение нагрузку с малым моментом инерции J (рис.1.13б). Переходный процесс описывается выражением
где 
- резонансная частота с учётом затухания колебаний.
График переходного процесса приведён на рис.1.14б. Чем меньше значение параметра ξ, тем медленнее затухает переходный процесс. Время переходного процесса можно определить только графически.
Частотные характеристики
и их графики, приведенные на рис.1.16. При ξ >0,707 резонансный пик на АЧХ отсутствует. При ξ <0,5 на ЛАЧХ имеется резонансный пик высотой Н.
Вопросы и задания
1. Что принято считать типовым звеном?
2. Приведите примеры безинерционных звеньев и их характеристики (передаточные функции, переходный процесс, частотные характеристики).
3. Приведите примеры апериодических звеньев 1-го порядка и их характеристики.
4. Приведите примеры апериодических звеньев 2-го порядка и их характеристики.
5. Приведите примеры колебательных звеньев и их характеристики.
1.6. Типовые дифференцирующие звенья САУ
К дифференцирующим звеньям относят звенья, выходной сигнал которых пропорционален производной от входного сигнала. У дифференцирующих звеньев нет статической характеристики, так как связь между входным и выходным сигналами не взаимно-однозначная, а именно, для любого постоянного входного сигнала выходной сигнал в установившемся режиме будет нулевым.
Виды типовых дифференцирующих звеньев:
1. Идеальное дифференцирующее звено имеет передаточную функцию вида
где 
– коэффициент размерности;
Т – постоянная времени дифференцирующего звена.
Примерами звена являются: тахогенератор (рис.1.17а) с малоинерционным ротором, входным сигналом которого является угол φ поворота ротора, а выходным – э.д.с. е; Д-регулятор на базе операционного усилителя ОУ (рис.1.17б).
Э.д.с. тахогенератора еТГ, как известно, прямо пропорциональна частоте вращения ω его ротора, которая равна производной 
от угла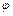 
поворота ротора:
Изображение и оригинал переходного процесса имеют вид
где δ (t)– дельта-функция (см. рис.1.3).
График переходного процесса (рис.1.18) представляет собой импульс бесконечно высокий и бесконечно узкий, площадь которого равна kT. Такой сигнал физически нереализуемый и фактически импульс всегда ограничен по амплитуде. Если входной сигнал х изменяется не скачком, то на выходе идеального дифференцирующего звена образуется сигнал у конечной формы. Например, при линейно изменяющемся входном сигнале x=v.t, изображением которого согласно табл.1.1 равно 
, изображение выходного сигнала будет 
, а оригинал согласно табл.1.1 будет равен 
.
Частотные характеристики
и их графики, приведенные на рис.1.19.
Самым ценным свойством идеального дифференцирующего звена является обеспечение им положительного фазового сдвига +90о. Благодаря этому сдвигу обеспечивается устойчивость САУ, повышается быстродействие и подавляется колебательность (раскачивание) САУ.
1. Реальное (инерционное) дифференцирующее звено имеет передаточную функцию вида
где τ – постоянная времени инерции дифференцирующего звена.
Примерами звена являются: тахогенератор (рис.1.17а) с инерционным ротором; дифференцирующие RC -цепь (рис.1.20а) и RL -цепь (рис.1.20б); гидравлический демпфер-амортизатор (рис.1.20в).
Выполним вывод передаточной функции для RC- цепи. Используя закон Ома, получим
Переходный процесс описывается выражением
График переходного процесса приведён на рис.1.21. От начального значения hнач сигнал стремится к нулю при t®¥. Время переходного процесса tпп, определяемое по моменту окончательного вхождения графика в 5% зону допуска от hнач, составляет 3τ.
Частотные характеристики
,
и их графики, приведенные на рис.1.22.
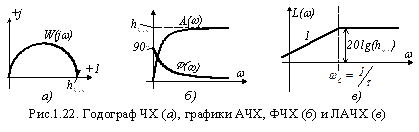
Фазовый сдвиг звена остается положительным, что благоприятно сказывается на устойчивости, быстродействии САУ, содержащих дифференцирующие звенья.
Вопросы и задания
1. Приведите примеры идеальных дифференцирующих звеньев и их характеристики (передаточные функции, переходный процесс, частотные характеристики).
2. Приведите примеры реальных (инерционных) дифференцирующих звеньев и их характеристики.
3. Какое положительное качество имеют дифференцирующие звенья?
1.7. Типовые интегрирующие звенья САУ
К интегрирующим звеньям относят звенья, выходной сигнал которых пропорционален интегралу от входного сигнала. У интегрирующих звеньев нет статической характеристики, так как связь между входным и выходным сигналами не взаимно-однозначная, а именно, при нулевом входном сигнале величина выходного сигнала в установившемся режиме может быть любой.
Виды типовых интегрирующих звеньев:
1. Идеальное интегрирующее звено имеет передаточную функцию вида
где k – коэффициент размерности; Т – постоянная времени звена.
Примерами звена являются: двигатель постоянного тока (рис.1.23а) с малоинерционным ротором, входным сигналом которого напряжение питания uя якоря, а выходным – угол φ поворота ротора; И-регулятор на базе операционного усилителя ОУ (рис.1.23б).
Изображение и оригинал переходного процесса имеют вид
График переходного процесса (рис.1.23в) представляет собой прямую линию.
Частотные характеристики
и их графики, приведенные на рис.1.24.
Самым большим недостатком идеального интегрирующего звена является отрицательный фазовый сдвиг -90о. Из-за этого сдвига САУ, содержащая идеальное интегрирующее звено, может стать неустойчивой, повышаются колебательность (раскачивание) САУ, перерегулирование.
2. Реальное (инерционное) интегрирующее звено имеет передаточную функцию вида
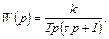
где τ – постоянная времени инерции интегрирующего звена.
Примерами звена являются: двигатель постоянного тока (рис.1.23а) с инерционным ротором; гидравлический сервопривод (рис.1.25а), у которого входным сигналом является давление масла рм, а выходным – перемещение у штока силового поршня.
Изображение и оригинал переходного процесса имеют вид
График переходного процесса приведен на рис.1.25б.
Частотные характеристики
и их графики, приведенные на рис.1.26.
3. Изодромное звено имеет передаточную функцию вида
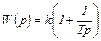(1.43)
Примерами звена являются: пропорционально-интегральный (ПИ) регулятор на базе ОУ (рис.1.27а); упруго присоединенный катаракт (рис. 1.27б), у которого входным сигналом х является сила F, а выходным – перемещение у точки, к которой приложена эта сила. Передаточную функцию (1.43) можно преобразовать к виду
,
из которого следует, что изодромное звено эквивалентно двум последовательно соединенным звеньям (рис.1.27в): идеальному интегрирующему звену с передаточной функцией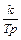 
и звену, содержащему пропорциональное и идеальное дифференцирующее звено, с передаточной функцией (Тр+1).
Изображение и оригинал переходного процесса имеют вид
График переходного процесса приведен на рис.1.28.
В начале переходного процесса наблюдается скачок величиной k, а затем от него выходной сигнал изменяется по линейной зависимости.
Частотные характеристики
и их графики, приведенные на рис.1.29.
В сравнении с другими интегрирующими звеньями изодромное звено имеет существенно меньший отрицательный фазовый сдвиг, что отчасти следует из эквивалентной структурной схемы звена, приведенной на рис.1.27в, в которую входит дифференцирующий блок (Тр+1). Значит, проблем с неустойчивостью САУ и другими плохими динамическими показателями, можно избежать.
Вопросы и задания
1. Приведите примеры идеальных интегрирующих звеньев и их характеристики (передаточные функции, переходный процесс, частотные характеристики).
2. Приведите примеры реальных (инерционных) интегрирующих звеньев и их характеристики.
3. Приведите примеры изодромных звеньев и их характеристики.
4. Какое положительное качество имеют изодромные звенья?
1.8. Структурные схемы САУ и их преобразования
В САУ, как видно из рис.В.1, входят различные элементы, каждый из которых имеет свою передаточную функцию. Соединение звеньев между собой, изображенных в виде прямоугольников с обозначением в них передаточных функций звеньев, называется структурной схемой САУ (рис.1.30 и т.д.). Со структурными схемами проводятся различные преобразования, среди которых основным является сворачивание структурной схемы в одно звено с эквивалентной передаточной функцией Wэкв . Существуют 3 типовых схемы соединения звеньев, который сворачиваются в одно звено за один приём без каких-либо дополнительных преобразований. Это - последовательное, параллельное соединения и соединение с обратной связью (рис.1.30).
Последовательное соединение на примере 3-х звеньев изображено на рис.1.30а. На линиях связи между звеньями не должно быть ни точек ветвления, ни точек слияния. Звенья друг относительно друга могут располагаться на чертеже под любым углом, могут располагаться также встречно, главное их связи между собой. Эквивалентная передаточная функция равна
Вывод этой формулы достаточно прост
Параллельное соединение на примере 3-х звеньев изображено на рис.1.30б. Главным в этом соединении звеньев является то, что все они имеют один и тот же входной сигнал, а выходные сигналы звеньев суммируются алгебраически на элементе - сумматоре. Варианты изображения сумматора сигналов показаны на рисунке, причём в варианте с секторами затемняется сектор, в котором сигнал является вычитаемым. Эквивалентная передаточная функция равна
Соединения с обратной связью на примерах отрицательной обратной связи (сигнал, пропорциональный выходному сигналу, вычитается из входного сигнала) и положительной обратной связи (сигнал, пропорциональный выходному сигналу, складывается с входным сигналом) изображены, соответственно, на рис.1.30в и рис.1.30г.
Эквивалентная передаточная функция равна
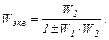(1.44)
где знак "+" при отрицательной, а знак "-" при положительной обратной связи.
Для соединения с отрицательной обратной связью вывод формулы (1.44) следующий. Согласно схемы рис.1.30в составим выражение
Из него находим отношение у/х, которое будет равно Wэкв согласно (1.44).
Если структурная схема не содержит рассмотренных типовых соединений, то их нужно создавать путём структурных преобразований.
В структурных схемах имеются объекты трёх видов: изображения звеньев, точки ветвления и точки слияния - суммирования/вычитания (рис.1.31).
Имеется 4 способа структурных преобразований, позволяющих свернуть любую структурную схему САУ:
1. Преобразования точек ветвления согласно рис.1.31а.
2. Преобразования точек слияния согласно рис.1.31б.
При этих преобразованиях количество звеньев структурной схемы не изменяется.
3. Переносы точки ветвления по цепи звеньев вперёд или назад согласно рис.1.31в.
4. Переносы точки слияния по цепи звеньев вперёд или назад согласно рис.1.31г.
При этих переносах точек ветвления и слияния в схему добавляется одно новое звено. Передаточная функция дополнительного звена должна быть такой, чтобы ни один выходной сигнал преобразованной структурной схемы не изменился. Это правило отражено на рис.1.31в и рис.1.31г.
