Методы ТАУ позволяют рассчитать реакцию на любое входное воздействие, однако систематизированные результаты, обладающие некоторыми закономерностями, можно получить для ограниченного ряда входных сигналов. В качестве типовых входных сигналов рассматривают те, которые чаще всего встречаются на практике, а также в некотором смысле являются наиболее сложными для отработки их САУ.
Реакция на единичный скачок 1(t) - переходной процесс h(t) (рис.1.2)
В электрических системах единичному скачку соответствует включение напряжения питания. Этот вид сигнала является для системы наиболее тяжелым для отработки. Если система отработает этот сигнал с заданными показателями качества, то наверняка будет качественно работать при других плавно изменяющихся сигналах.
Реакция на дельта-импульс d(t) - функция веса k(t) (рис.1.3)
Дельта-импульс d(t) имеет нулевую длительность, бесконечную амплитуду и единичную площадь (S=1). Дельта-импульсу соответствует помеха в электрических схемах и удар в механических системах. Математический аппарат и свойства функции веса широко используется в расчётах импульсных САУ.
Реакция на гармонический сигнал - частотные характеристики (рис.1.4)
Если на вход линейной системы воздействует гармонический сигнал с амплитудой Xm и фазой jx, то на выходе будет сигнал той же частоты, однако другой амплитуды Ym и фазы jy.
Изменения амплитуды Ym и фазы jy выходного сигнала y(t) зависят от частоты w входного сигнала x(t). Эти зависимости определятся следующие частотные характеристики: АЧХ (амплитудно-частотную) и ФЧХ (фазо-частотную):
АЧХ: 
- коэффициент передачи (усиления) звена на данной частоте, равный отношению амплитуд сигналов;
ФЧХ: 
- сдвиг по фазе между выходным и входным сигналами.
Частотные характеристики очень просто находятся с использованием выражения передаточной функции W(p) (см. тему 1.3).
Вопросы и задания
1. Поясните смысл и необходимость линеаризации уравнений звеньев САУ.
2. Линеаризуйте произвольно заданное нелинейное дифференциальное уравнение.
3. Поясните распространенные в САУ формы записи дифференциальных уравнений. Как перейти от одной формы записи к другой?
4. Назовите типовые воздействия, принятые в САУ, и назовите реакции на них.
1.2. Методы расчета переходных процессов,
функции веса и построения графиков
переходных процессов
Понятие переходного процесса является одним из важнейших понятий ТАУ, и особенно теории линейных систем. Поэтому умение легко, практически автоматически, рассчитывать переходный процесс во многом определяет успех дальнейшего понимания ТАУ.
Как известно, передаточная функция звена – это отношение изображения по Лапласу выходного сигнала к изображению входного, которыми в частном случае могут быть переходный процесс h(p) и единичный сигнал 1(p)=1/p,
Из этого следует, что изображение переходного процесса
(1.9)
Аналогично для функции веса
и 
(1.10)
По свойству преобразования Лапласа, умножение изображения на p, соответствует первой производной от оригинала. Поэтому функция веса определяется также как производная от переходного процесса:
(1.11)
Заметим еще раз, что все функции комплексной переменной p - h(p), k(p) и т.д., являются изображениями соответствующих функций действительной переменной t - h(t), k(t) и т.д.
Примеры расчетов переходных процессов и функции веса
Далее расчёты переходного процесса, функции веса с построением их графиков выполним на числовых примерах.
Вид переходного процесса определяется корнями характеристического уравнения, образуемого приравниванием к нулю либо многочлена знаменателя передаточной функции, либо сомножителя при у(р) в операторном уравнении.
I. Корни характеристического уравнения действительные.
Пусть задана передаточная функция САУ
Решение.
1. Раскладываем знаменатель на простейшие сомножители
Решаем относительно p характеристическое уравнение
Оно имеет следующие действительные корни:
Следовательно, характеристический многочлен можно разложить на множители следующим способом:
(1.12)
2. Определяем оригинал табличным способом
Представляем выражение h(p) в виде суммы простейших дробей, оригиналы для каждой из которых имеются в таблице 1.1:
(1.13)
Чтобы коэффициенты при степенях p в левой и правой частях равенства (1.13) были бы одинаковыми, необходимо:
Приравняв коэффициенты при одинаковых степенях p, получаем:
Решая, эту систему уравнений, получаем:
Окончательно получаем разложение h (p)на табличные выражения:
Перейдя согласно табл.1.1 от изображений к оригиналам, получим:
(1.14)
и для функции веса:
(1.15)
3. Строим графики переходного процесса и функции веса
Для построения графика надо определить время счета и шаг изменения времени.
Определение времени счета
Приводим выражение h (t) к стандартному виду, так что бы свободный член был равен 1:
(1.16)
На бесконечности 
значение h (t)стремится к установившемуся значению hуст=3, так как обе экспоненты в выражении (1.16) обращаются в нуль.
Находим время переходного процесса для каждой из экспонент.
Переходный процесс считается завершенным, когда его график h (t) попадает в 5%-зону установившегося значения, и далее не выходит из нее. В представлении переходного процесса в виде (1.16) установившееся значение для выражения, заключённого в скобки, равно 1. Поэтому время tпп1, в течение которого затухает 1-я экспонента, находится из уравнения
Аналогично находим время переходного процесса для 2-й экспоненты: 
Время tпп всего переходного процесса не равно ни tпп1, ни tпп2, но меньше большего из этих двух значений. Точное значение tпп можно найти только из графика переходного процесса. Для аналитического его определения потребовалось бы решить трансцендентное уравнение, что невозможно.
Определение шага вычислений
Шаг вычислений Δt выбираем таким образом, чтобы объём вычислений был минимальный и достаточный для построения графика. Здесь используется практическое правило: для построения гладкого графика вручную достаточно иметь 5-10 точек графика, через которые затем "на глаз" проводится весь график.
Согласно оценке (1.17) времени tпп1 для построения составляющей графика h (t), соответствующей 1-й экспоненте, шаг вычислений Δt1 должен быть равен 0,32...0,64 с. Аналогично, основываясь на оценке tпп2, находим Δt2=0,04...0,08 с. Поэтому в интервале изменения t от 0 до 0,4 с вычисления ведём с шагом Δt1=0,08 с, а далее до времени 3,2 с - с шагом Δt2=0,4 с.
Функцию веса k (t) рассчитываем по выражению (1.15) при тех же значениях t, которые использовались при вычислении h (t).
Результаты вычислений сводятся в таблицу 1.2.
Таблица 1.2
| t | 0 | 0,08 | 0,16 | 0,24 | 0,32 | 0,4 | 0,8 | 1,2 | 1,6 | 2 | 2,4 | 2,8 | 3,2 | 
|
| h (t) | 0 | 3 | ||||||||||||
| k (t) | 1 | 0 |
По данным этой таблицы строятся графики h (t)и k (t) (рис.1.5).
II. Корни характеристического уравнения комплексные
Этапы расчётов те же, что и в предыдущем примере, поэтому нумерацию этапов и названия далее не приводим.
Пусть задана передаточная функция
Решаем характеристическое уравнение
Корни комплексные, поэтому далее решение идет по другому пути.
Выделяем полный квадрат в знаменателе, а затем, как и раньше раскладываем выражение h (p) на сумму табличных выражений:
Из равенства второй и последней дробей получаем систему уравнений, использемую для расчета значений коэффициентов А, В и С,
Решая, эту систему уравнений, получаем:
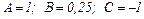
Окончательно изображение переходного процесса примет вид:
Переходим согласно табл.1.1 от изображений к оригиналам:
(1.17)
Далее находим функцию веса:
(1.18)
Определение времени счета:
Преобразуем выражение h (t)(1.17) следующим образом:
(1.19)
Сумму в скобке можно представить в виде одной функции sin:
(1.20)
Мы имеем право на замену дробей 0,242 и 0,97 на cosg и sing, соответственно, т.к. сумма их квадратов равна 1: 0,2422+0,972=1. Это свойство коэффициентов при sinw t и cosw t (в данном случае w=2) в выражении (3.28) верно всегда при выполнении преобразований, приведенных в этом выражении.
C учетом (1.20) h (t) можно представить в таком виде:
,
где 
рад (вычислить g можно по любой формуле из приведенного их ряда).
Окончательно:
(1.21)
Так как функция sin по модулю не превосходит 1, то время переходного процесса можно вычислить так же, как и раньше, из уравнения:
(1.22)
График переходного процесса колебательный и будет содержать экстремальные точки. Для их нахождения используется производная от h (t), т.е. функция веса k (t):
k (t) =0, 1,875e-0,5tsin2t+e-0,5tcos2t=0, tg2t=-1/1,875=-0,533,
откуда
te=(arctg(-0,533)+pn)/2=-0,245+pn/2 (рад), где n=1,2,3...
Значения te: te1=1,325 c, te2=2,9 c; te3=4,465 c, te4=6,03 c и т.д.
Определение шага вычислений:
Из времени tпп=6,1 с находим шаг вычислений D t=1с; Время счета t = 0..7.
Далее заполняется таблица (табл.1.3) вычислений при найденных значениях t и затем строятся графики h (t)и k (t) (рис.1.6).
Таблица 1.3
| t | 0 | 1,325 | 2 | 2,9 | 3,7 | 4,465 | 5 | 6,03 | 7 | ∞ |
| h (t) | 0 | 1 | ||||||||
| k (t) | 1 | 0 |
Вопросы и задания
1. Обоснуйте вид изображений переходного процесса h (t) и функции веса k (t), а также связи между ними
2. Поясните суть табличного метода расчета переходного процесса h (t).
3. Как определяются время tПП переходного процесса и шаг вычислений при расчете и построениях графика переходного процесса h (t) при действительных корнях характеристического уравнения передаточной функции?
4. Как определяются время tПП переходного процесса и шаг вычислений при расчете и построениях графика переходного процесса h (t) при комплексных корнях характеристического уравнения передаточной функции?
5. Как определяются экстремальные точки графика колебательного переходного процесса h (t)?
1.3. Частотные характеристики линейных САУ
Частотные характеристики линейных САУ рассчитываются через передаточные функции: если W (p) – передаточная функция, то W (jw)– частотная характеристика (ЧХ), получаемая из передаточной функции путём замены в ней p на jw.
ЧХ как комплексное число может быть представлено в показательной и алгебраической формах.
Показательная форма:
(1.22)
Эта запись позволяет найти еще две важнейшие характеристики: АЧХ и ФЧХ:
A (w) – амплитудо-частотная характеристика (АЧХ);
j (w) – фазо-частотная характеристика (ФЧХ).
Алгебраическая форма:
W(jw) =P (w) +jQ (w) (1.23)
Данное выражение порождает еще две характеристики: 
– вещественно-частотная характеристика (ВЧХ) и 
– мнимо-частотная характеристика (МЧХ).
График ЧХ на комплексной плоскости называется годографом (рис.1.7).
Между величинами A, j, P и Q существуют связи (аргумент w опущен):
(1.24)
Особенности вычислений ЧХ можно проследить только на числовом примере.
Пусть передаточная функция звена имеет вид
Частотная характеристика
(1.25)
В записи (1.25) ЧХ формально представляет собой отношение двух комплексных чисел числителя и знаменателя.
Считая (1.25) показательной формой записи ЧХ, вычисляем АЧХ и ФЧХ:
- АЧХ: 
(1.26)
- ФЧХ: 
(1.27)
ВЧХ и МЧХ рассчитываем, используя домножение числителя и знаменателя ЧХ на комплексно-сопряженное к знаменателю число:
откуда
(1.28)
Как видно, вывод выражений A (w), j (w), P (w)и Q (w)принципиально прост. Сложным являются вычисления координат точек годографа ЧХ, если принять во внимание, что при этих вычислениях нужно знать:
- до какого значения аргумента w нужно считать (полный интервал изменения w от 0 до ¥)?;
- и каким должен быть шаг Dw вычислений?
В сравнении с расчётами переходных процессов расчёты ЧХ сложнее тем, что нет простых процедур определения конечной (верхней) частоты w счёта и шага Dw. Последний, к тому же, будет неравномерным.
Здесь следует пользоваться проверенными на практике приёмами расчёта ЧХ:
1. Необходимо предугадать вчерне вид годографа, а именно, где его начало и конец, через какие квадранты комплексной плоскости и в каком порядке он пройдёт при изменении частоты w от 0 до ¥.
Прежде всего, находят точки пересечения годографа с осями координат. Для этого решают уравнения:
P (w) =0 Þ -w4+2w2+9=0 Þ w=2,04, т.е. годограф пересекает мнимую ось на частоте w5=2,04, если в качестве иллюстрации расчётов принять рис.1.7;
Q (w) =0 Þ w(0,5w2+1,5) =0 Þ w=0, т.е. годограф пересекает действительную (вещественную) ось на частоте w1=0.
Далее вычисляют значения P (w)и Q (w)при найденных частотах и на бесконечности при w=¥.
2. Определяют значение угла j (¥), с которым годограф входит в начало координат, по формуле
j (¥) =-90o (n-m), (1.29)
где n и m - степени полиномов p, соответственно, знаменателя и числителя передаточной функции.
По результатам описанных вычислений строится в черновом варианте годограф ЧХ (рис.1.7).
3. Подготавливается таблица вычислений, состоящая из 5-ти строк (табл.1.4).
Таблица 1.4
| w | w1=0 | w2 | w3 | w4=2,04 | w5 | w6 | w7 | w=¥ |
| P (w) | 0 | 0 | ||||||
| Q (w) | 0 | 0 | ||||||
| A (w) | 0 | |||||||
| j (w) | 0 | -90o | -180o |
В этой таблице прежде всего нужно заполнить первую строку - строку частот w. Все остальные строки затем заполнятся вычислениями по формулам (1.26)...(1.28).
Сначала находим частоты w2 и w3 для точек годографа, лежащих в 4-м квадранте. Очевидно, что эти частоты должны быть такими, чтобы точки годографа на этих частотах равномерно заполняли бы участок в 4-м квадранте, т.е. угол j между соседними точками был примерно равен 30о (ни в коем случае не надо стремиться получить точно 30о, а лучше задать, например, 30о 
10о). Руководствуясь этими соображениями, задаёмся частотой в пределах от 0 до 2,04 (эти значения верны только для рассматриваемого числового примера!) и вычисляем угол j. Если он равен 30о 10о, то нами найдена (точнее - угадана) частота w2. Если вычисления дали 60о 10о, то найдена частота w3. Иначе нужно снова задать значение w. Аналогично определяют частоты w5...w7 для 3-го квадранта.
После заполнения строки частот заполняется значениями вся таблица. По значениям P (w) и Q (w) строится годограф W (jw)(рис.1.7), а по значениям A (w)и j (w)строятся АЧХ и ФЧХ (рис.1.8).
Замечание к расчётам по формуле (4.7) значений угла j на калькуляторе, компьютере и по таблицам тригонометрических функций. Во всех перечисленных случаях определяется только главные значения арктангенса - ARCTG (*), - которые находятся в пределах от -90о до +90о. Действительное значение угла определяется с учётом структуры выражения, находящегося под знаком arctg, которое является отношением мнимой Q к действительной P части соответствующего комплексного числа. Если P>0, то угол лежит в 1-м или 4-м квадрантах, если P<0, то угол лежит во 2-м или 3-м квадрантах. При Р=0 угол равен 90о:
где sign (Q)- знак числа Q.
Как видно из приведенных выше приёмов расчёта ЧХ такой расчёт содержит достаточно громоздкие вычисления.
Вопросы и задания
1. Что такое "показательная" и "алгебраическая" формы записи ЧХ? Как перейти от одной формы записи к другой?
2. Как по заданной передаточной функции рассчитать выражения АЧХ А (ω) и ФЧХ φ (ω)?
3. Каковы практические приемы расчета частотных характеристик?
4. Почему при вычислениях ФЧХ φ (ω) требуется коррекция и какова эта коррекция?
1.4. Логарифмические амплитудно-частотые
характеристики - ЛАЧХ
Из частотных характеристик в ТАУ чаще всего используются асимптотические логарифмические амплитудно-частотные характеристики (ЛАЧХ). Преимущество асимптотических ЛАЧХ (далее – просто ЛАЧХ) в том, что их расчёт чрезвычайно прост при достаточно высокой точности. При использовании ЛАЧХ не существует проблем с длительным выбором (угадыванием) частот, при которых следует выполнять вычисления.
ЛАЧХ определяется выражением
, (1.30)
а асимптотической она становится благодаря специальным правилам ее построения, суть которых в том, что:
- оси координат полулогарифмические, а именно, ось ω логарифмическая неравномерная, а ось L (ω) линейная равномерная;
- ЛАЧХ состоит из отрезков прямых линий со стандартными коэффициентами наклона.
Для построения ЛАЧХ необходимо передаточную функцию W (p) привести к стандартной форме
(1.31)
Например,
Далее из (1.31) образуем АЧХ
(1.32)
В выражении АЧХ (1.32) будут всегда присутствовать максимум только четыре стандартных сомножителя видов
(1.33)
Для радикалов 
, которым в исходной передаточной функции (1.31) соответствуют скобки выражений двух- и трехчленов 
введем приближенные замены:
1) 
(1.34)
или для скобки двучлена
(1.35)
Обозначим 
и назовем её частотой сопряжения участков ЛАЧХ. Максимальная погрешность замен (1.34) достигается на частоте сопряжения и составляет 3 дБ. Это малая величина, если оценивать ее по реальным графикам ЛАЧХ (рис.1.9).
2) 
(1.36)
или для скобки трехчлена
(1.37)
