Пример сворачивания структурной схемы приведён на рис.1.32.
Исходная схема а (рис.1.32а) не имеет типовых соединений звеньев. Схема б получена из схемы а переносом назад по цепи элементов W2 и W3 точки ветвления 4. Добавлено звено W3. Схема в получена из схемы б заменой соединения с положительной обратной связью звеном W4. Схема г получена из схемы в заменой последовательно соединенных и охваченных единичной отрицательной обратной связью звеньев W1 и W4 одним звеном W5. Схема д - конечная.
Приводим вычисления по структурным преобразованиям, отображенным на рис.1.32:
Вопросы и задания
1. Какие соединения звеньев называются типовыми? Приведите их эквивалентные передаточные функции.
2. Поясните назначение структурных преобразований схем САУ. Поясните структурные преобразования над точками ветвления.
3. Поясните назначение структурных преобразований схем САУ. Поясните структурные преобразования над точками слияния.
4. Поясните на рассмотренном примере процедуры преобразования и расчеты эквивалентной передаточной функции.
5. Приведите свой вариант сворачивания структурной схемы примера.
1.9. Понятие об устойчивости САУ. Прямые методы
устойчивости. Критерий устойчивости Гурвица.
Определение допустимых настроек САУ
САУ называется устойчивой, если при t®¥ переходный процесс стремится к установившемуся значению. Учитывая то, что в линейных САУ по существу рассматриваются линеаризованные системы, то указанный вид устойчивости справедлив при малых отклонениях от первоначального устойчивого состояния. Эту устойчивость называют также "устойчивостью в малом". Иллюстрации такой устойчивости приведены на рис.1.33.
Свойство устойчивости для САУ является обязательным, так как неустойчивая САУ фактически неработоспособна.
Устойчивость можно оценить прямыми методами или при помощи критериев устойчивости.
Прямые методы оценки устойчивости.
Свойство устойчивости может быть определено по графику переходного процесса (рис.1.33г). Однако расчёт и построение графика переходного процесса требует больших вычислений.
Проще установить устойчивость без построения графика h (t), а только по корням характеристического уравнения изображения переходного процесса h (p). Каждому корню характеристического уравнения соответствует свой член, входящий как слагаемое в выражение h (t)переходного процесса. В таблице 1.5 приведены соответствия корней характеристического уравнения САУ, вид слагаемых в выражении переходного процесса и характеристики устойчивости САУ.
Оценка устойчивости либо по графику переходного процесса, либо по корням характеристического уравнения имеет тот недостаток, что её невозможно в общем случае применить к САУ, в передаточной функции которой содержится хотя бы один буквенный коэффициент, так как не существует аналитических методов решения алгебраических уравнений (именно таким уравнением является характеристическое уравнение САУ) выше 3-й степени. По этой же причине неприменима указанная оценка устойчивости на этапе синтеза САУ.
Оценка устойчивости при помощи критериев устойчивости.
В ТАУ для оценки устойчивости применяются критерии устойчивости. Критериями устойчивости называются совокупность процедур и правил, с помощью которых можно установить факт устойчивости САУ без нахождения корней характеристического уравнения. Существуют различные виды таких критериев как алгебраических, так и частотных. Ниже рассмотрены наиболее применимые в ТАУ критерии Гурвица, Михайлова и Найквиста.
Таблица 1.5
| Тип корня характеристического уравнения | Слагаемое в выражении h(t) | Переходный процесс h(t) |
| 1. p=0 | С | Устойчив |
| 2. p1=0, p2=0 (два нулевых корня) | С×t | Неустойчив |
| 3. p=a (действительный корень) | 
| Устойчив при a<0 и неустойчив при a>0 |
| 4. p=a±jb (комплексные корни) | 
| Устойчив при a<0 и неустойчив при a>0 |
| 5. p=±jb (корни чисто мнимые) | 
| На грани устойчивости |
Критерий устойчивости Гурвица
Критерий Гурвица является алгебраическим. Для оценки устойчивости используется характеристический многочлен передаточной функции замкнутой САУ. Структура САУ может быть любой.
Вводная часть к критерию Гурвица.
Пусть замкнутая САУ имеет следующую передаточную функцию
Из коэффициентов характеристического многочлена
составляем следующую матрицу
(1.45)
Порядок заполнения матрицы следующий. Сначала по диагонали матрицы располагают коэффициенты от a1 до an. Затем над диагональными элементами располагают коэффициенты с возрастающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0. Далее под диагональными элементами располагают коэффициенты с убывающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0.
Формулировка критерия Гурвица: САУ устойчива, если:
1) положительны все коэффициенты характеристического многочлена;
2) положительны все n главных (диагональных) определителей Гурвица матрицы (1.45):
(1.46)
Последний определитель не вычисляют, так как его знак совпадает со знаком Δn-1:
Δn=an×Δn-1
Если хотя бы один определитель Гурвица отрицателен, то САУ неустойчива. Если имеется хотя бы один определитель Гурвица равен нулю при остальных положительных, то САУ находится на границе устойчивости.
Числовой пример.
Определить устойчивость САУ с передаточной функцией
(1.47)
Составляем матрицу Гурвица и главные определители
Оба определителя положительны, поэтому САУ устойчива.
Определение допустимых настроек САУ.
Если передаточная функция САУ содержит хотя бы один буквенный коэффициент, значение которого может быть любым числом, то с помощью критерия Гурвица можно определить допустимые по условию устойчивости значения такого коэффициента. При двух буквенных коэффициентах возможно совместное определение допустимых значений таких коэффициентов и выделение областей устойчивости на плоскости этих коэффициентов. Покажем это на примере.
Пусть САУ управления курсом судна, представленная на рис.1.34, состоит из двух звеньев - авторулевого и судна. Передаточные функции авторулевого и судна имеют вид, соответственно,
Постоянная времени T судна зависит от загрузки судна и изменяется от 10 с при порожнем судне до 60 с при полностью загруженном. Параметром настройки авторулевого является коэффициент передачи K. Необходимо найти такие значения параметра K, при которых САУ устойчива при изменении загрузки судна.
Определяем передаточную функцию замкнутой САУ
(1.48)
Составляем матрицу Гурвица и вычисляем 2-й определитель:
(1.49)
С учётом положительности всех коэффициентов характеристического многочлена при условии (1.49) САУ будет устойчива при одновременном выполнении следующей системы неравенств
(1.50)
САУ будет находиться на границе устойчивости, если будет выполнено хотя бы одно из равенств
. (1.51)
Каждое из равенств (1.51) является на плоскости T-K границей области устойчивости (рис.1.35). Штриховкой обозначены области устойчивости по отношению к линиям границы устойчивости. Общая область a0d для всех заштрихованных областей является областью устойчивости САУ.
Пусть при порожнем судне с Тпорож установлен коэффициент передачи K1 регулятора. Этот состояние САУ отмечено точкой 1, лежащей в области устойчивости. Если после загрузки судна значение T увеличится до Tгруж, то при том же K1 САУ в точке 2 будет неустойчива. Необходимо будет увеличить K до значения K3, чтобы система оказалась в точке 3. Область, ограниченная ломаной линией abcd, будет областью устойчивости при любой загрузке судна.
Вопросы и задания
1. Дайте определение устойчивости. Назовите прямые методы устойчивости и дайте характеристику области их применимости.
2. Что представляют собой критерии устойчивости? В чем состоят их преимущества перед прямыми методами?
3. Приведите формулировку критерия устойчивости Гурвица и продемонстрируйте его использование для оценки САУ 3-го порядка с произвольной передаточной функцией.
4. Поясните процедуры определения допустимых настроек САУ по условию устойчивости.
1.10. Критерий устойчивости Михайлова.
Определение допустимых настроек САУ
Критерий Михайлова является частотным. Для оценки устойчивости используется характеристический многочлен передаточной функции замкнутой САУ. Структура САУ может быть любой.
Подготовительные операции.
Пусть замкнутая САУ имеет следующую передаточную функцию
Из коэффициентов характеристического многочлена
образуем годограф Михайлова
(1.52)
Вычисляем и строим годограф D(jω) при значениях ω = 0 … ∞ (рис.1.36).
Формулировка критерия Михайлова: САУ п -го порядка устойчива, если годограф Михайлова, начинаясь на положительной части действительной оси, проходит против часовой стрелки подряд ровно п квадрантов (рис.1.36а). Если годограф проходит п квадрантов не подряд или проходит меньше квадрантов, чем п, то САУ неустойчива (рис.1.36б). Если годограф при любой частоте проходит через начало координат, то САУ находится на грани устойчивости (рис.1.36в).
Оценка устойчивости с использованием графика годографа Михайлова наглядна, но требует громоздких вычислений по выражению (1.52). Если учесть, что для оценки устойчивости важен только факт прохождения годографом п квадрантов против часовой, а не сама форма годографа (рис.1.36а), то на этом можно существенно сократить вычисления. Достаточно найти частоты ω1, ω2, …, ωп, при которых пересекаются оси координат, упорядочить их по возрастанию и для этих частот найти последовательно знаки (+ или -) выражений Р(ω1), Q(ω2), P(ω3),…, где Р и Q - соответственно, действительные и мнимые части выражения W(jω). САУ будет устойчива, если знаки выражений Р и Q будут чередоваться согласно табл.1.6. Любое отступления от табл.1.6 свидетельствует о том, что САУ либо неустойчива, либо находится на грани устойчивости.
Числовой пример.
Определить устойчивость САУ с передаточной функцией (1.47). Характеристический многочлен от (1.47) и годограф Михайлова имеют вид
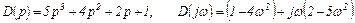
В точках пересечения годографа с действительной осью выполняется равенство
, откуда ω1=0 и 
Для этих частот рассчитываем значения Р (ω):
В точках пересечения годографа с мнимой осью выполняется равенство
, откуда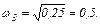 
Для этой частоты рассчитываем значение Q (ω):
Составляем таблицу по типу табл.1.6.
| ω | 0 | 0,5 | 0,632 |
| Р(ω) | + | 0 | - |
| Q(ω) | 0 | + | 0 |
Чередование знаков Р (ω) и Q (ω) правильное и, поэтому, САУ устойчива.
Определение допустимых настроек САУ.
Если передаточная функция САУ содержит хотя бы один буквенный коэффициент, значение которого может быть любым числом, то с помощью критерия Михайлова можно определить допустимые по условию устойчивости значения такого коэффициента. При двух буквенных коэффициентах возможно совместное определение допустимых значений таких коэффициентов и выделение областей устойчивости на плоскости этих коэффициентов. Покажем это на примере, рассмотрев САУ управления курсом судна, представленную на рис.1.34.
Характеристический многочлен согласно (1.48) и годограф Михайлова имеют вид
В точках пересечения годографа с действительной осью выполняется равенство
, откуда ω1=0 и 
.
Для этих частот рассчитываем значения Р (ω):
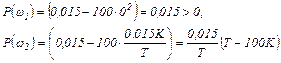
Значение Р (ω2) будет отрицательным числом при T<100K или K>0,01.T, что совпадает с (1.50). При этом соотношении 
или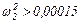 
.
В точках пересечения годографа с мнимой осью выполняется уравнение
, откуда 
Для этой частоты рассчитываем значение Q (ω):
при K>0,01.T.
Составляем таблицу по типу табл.1.6.
| ω2 | 0 | 0,00015 | >0,00015 |
| Р(ω) | + | 0 | - |
| Q(ω) | 0 | + | 0 |
Чередование знаков Р(ω) и Q(ω) правильное и, поэтому, САУ при K>0,01.T устойчива.
Вопросы и задания
1. Сформулируйте критерий устойчивости Михайлова и продемонстрируйте его использование для оценки САУ 3-го порядка с произвольной передаточной функцией.
2. Поясните процедуры определения допустимых настроек САУ по условию устойчивости.
1.11. Критерий устойчивости Найквиста.
Использование ЛАЧХ для оценки устойчивости САУ
Критерий Найквиста является частотным. САУ должна иметь структуру с единичной обратной связью (рис.1.37). Для оценки устойчивости используется частотная характеристика разомкнутой САУ.
Подготовительные операции.
Вычисляем и строим годограф Wраз (jω) частотной характеристики разомкнутой САУ при значениях ω = 0 … ∞ (рис.1.38).
Формулировка критерия Найквиста зависит от вида частотной характеристики Wраз (jω) разомкнутой САУ. Ниже рассмотрим только два вида Wраз (jω), которые чаще всего встречаются на практике.
1). Пусть разомкнутая САУ устойчива. Тогда замкнутая САУ будет устойчива, если годограф Wраз (jω) Найквиста, начинаясь на положительной части действительной оси, не охватывает точку –1 действительной оси (рис.1.38а). Если годограф охватывает точку –1 действительной оси (рис.1.38б), то САУ неустойчива (рис.1.38б), а если проходит через точку –1 действительной оси, то САУ находится на грани устойчивости (рис.1.38в).
2). Пусть разомкнутая САУ обладает астатизмом 1-го порядка, являясь САУ, находящейся на грани устойчивости. В этом случае начало годографа Wраз (jω) разомкнутой САУ при ω=0 находится на бесконечности (рис.1.39). Необходимо такой годограф дополнить дугой бесконечно большого радиуса, начинающейся на положительной части действительной оси и заканчивающийся на начале годографа Wраз (jω). Тогда к такому годографу применимы все правила, по которым оценивалась устойчивость как на рис.1.38.
Использование ЛАЧХ для оценки устойчивости САУ
Введем на построениях критерия устойчивости Найквиста косвенные показатели качества – запас по фазе γ и частоту среза ωср (рис.1.40). Запас по фазе γ характеризует удаленность годографа Wраз (jω) от точки с координатой –1 на вещественной оси. Для устойчивости САУ достаточно, чтобы запас по фазе был бы положительным. Чем больше запас по фазе, тем меньше перерегулирование на графике переходного процесса (см. рис.1.41). Считается для качественной САУ достаточно иметь запас по фазе в пределах 30о…50о.
Из построений, приведенных на рис.1.40, следует, что:
1) запас по фазе можно рассчитать по выражению частотной характеристики Wраз (jω), подставив в него значение частоты среза ωср.
2) на частоте среза ωср значение модуля частотной характеристики Wраз (jω) равно единице - 
, логарифм от такого модуля равен нулю -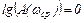 
и, следовательно, значение ЛАЧХ от частотной характеристики Wраз (jω) на частоте среза также равно нулю - 
;
3) запас по фазе γ и значение фазочастотной характеристики, вычисленное на частоте среза удовлетворяют равенству
, (1.53)
и, следовательно, запас по фазе определяется по выражению фазочастотной характеристики φ(ω), вычисленное при одной частоте – частоте среза ωср.
Описанные свойства построений, приведенных на рис.1.40, позволяют перейти к определению частоты среза из графика ЛАЧХ разомкнутой САУ (рис.1.41).
Частота среза определяется графически как точка пересечения ЛАЧХ L(ω) с осью частоты ω. Далее рассчитывается только одно значение фазы φ(ωсз) и по выражению (1.53) определяется запас по фазе γ.
Простота построения ЛАЧХ (см. тему 1.4), а также простота вычисления запаса по фазе, обусловливает простое использование критерия устойчивости Найквиста в следующей формулировке:
Замкнутая САУ устойчива, если запас по фазе для разомкнутой САУ положительный, неустойчива, если запас по фазе отрицательный и находится на грани устойчивости при нулевом запасе по фазе.
Вопросы и задания
1. Сформулируйте критерий устойчивости Найквиста для статической САУ.
2. Сформулируйте критерий устойчивости Найквиста для астатической САУ.
3. Какие косвенные показатели качества вводятся на построениях Найквиста?
4. Сформулируйте критерий устойчивости Найквиста, основанный на построениях ЛАЧХ.
1.12. Прямые показатели качества САУ. Расчет ошибок
регулирования. Статические и астатические САУ
Прямые показатели качества подразделяются на показатели качества динамического и установившегося режимов.
Показателями качества динамических режимов определяются из графика переходного процесса и основными из них являются (рис.1.42):
- перерегулирование или заброс σ, равный максимуму отклонения значения переходного процесса относительно установившегося значения процесса hycm;
- время первой установки t1, определяемое моментом первого пересечения графиком переходного процесса установившегося значения hycm;
- время переходного процесса tПП, определяемое момент окончательного входа графика переходного процесса в зону допуска, равную ±5% от установившегося значения процесса hycm.
Для всех названных динамических показателей качества невозможно в общем случае получить формулы для их расчета. Это является существенным препятствием для решения задач анализа и синтеза САУ.
Показателями качества установившихся режимов являются ошибки регулирования, равные абсолютной величине разности между заданным и фактическим значениями сигналов САУ и которые в зависимости от вида входного сигнала САУ подразделяются на статические (εСТ) и скоростные ошибки (εСК) и ошибки (εm) при отработке гармонического входного сигнала.
Для всех названных ошибок регулирования можно в общем случае получить формулы их расчета.
Из структурной схемы замкнутой САУ (рис.1.43) следуют выражения передаточной функции САУ Wε(p) по ошибке и изображения ε(р) ошибки регулирования:
Расчет ошибки εm отработки гармонического входного сигнала x=Xmsinωt производится по формуле
где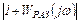 
- модуль комплексного числа 
.
Статическая (εСТ) и скоростная (εСК) ошибки равны установившимся значениям оригинала 
и 
, или в общем виде, по формуле 
. Значение вычисляют через изображение ε (р) по доказываемой в теории операционного исчисления формуле предельного перехода,
(1.54)
Выражение передаточной функции разомкнутой САУ в общем случае может быть приведено к виду:
(1.55)
где К – общий коэффициент усиления разомкнутой САУ:
ν - порядок астатизма САУ, причем ν является целым неотрицательным числом.
Для удобства вычислений по формуле (1.54) подставим в нее выражение WРАЗ(р) из (1.55) и выполним предельный переход:
(1.56)
Статическая ошибка регулирования εСТ рассчитывается при постоянном входном сигнале x (t) =X=const, а скоростная εСК - при входном сигнале x=Vt, изменяющемуся во времени с постоянной скоростью V=const. Далее расчеты статической (εСТ) и скоростной (εСК) ошибок выполним раздельно.
