(6)
матрицалық теңдеуді қарастырайық.
Егер 
ерекше емес квадрат матрица болса, онда бұл теңдеудің жалғыз шешімі болады: 
. Егер де кез келген 
-өлшемді тікбұрышты матрица болса, онда ізделінді 
шешімінің өлшемі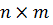 
болады, алайда бірмәнді анықталмайды. Жалпы жағдайда (6) теңдеудің шектеусіз шешімдер жиыны болады.
Анықтама 2.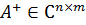 
матрицасы псевдокері немесе 
матрицасы үшін Мур-Пенроуздың жалпыланған кері матрицасы деп аталады, егер төмендегі шарттар орындалса:
(7)
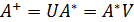(8)
Мұндағы 
, 
-қандай да бір матрицалар.
(8) шарт 
матрицасының жолы (бағаны) 
матрицаның жолының (бағанының) сызықты комбинациясы болатындығын білдіреді.
Лемма 5. Кез келген 
матрицасы үшін келесі теңдік орындалады:
(9)
Дәлелдеуі. Біріншіден, 
болғандықтан, онда матрицаларды көбейту ережесі бойынша 
мен 
матрицаларының диагональдық элементтері тең болатындығын оңай тексеруге болады.
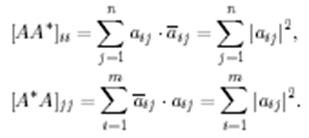(10)
Онда матрицаның ізінің анықтамасынан (10) ескеріп мынаны аламыз:
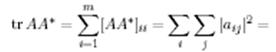
Бұдан (9) дұрыс болатындығы шығады.
Салдар 1. матрицасы үшін кез келген 
теңдіктерінен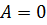 
болатындығы шығады.
Теорема 1. Кез келген матрицасы үшін Мур – Пенроуздың псевдокері матрицасы бар, жалғыз болады және келесі формуламен өрнектеледі:
(12)
мұндағы 
және 
- 
матрицасының (1) скелеттік жіктелуінің компоненттері.
Дәлелдеуі. матрицасының бар болуын дәлелдейік. Егер 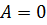болса, онда 
деп қояйық. Айталық, 
болсын. (1) жіктеуді қарастырайық және алдымен 
іздейік. Псевдокері матрицаның анықтамасынан мынаны аламыз:
Соңғы теңдікті сол жағынан 
-ға көбейтіп, мынаны аламыз:
Енді соңғы теңдікті оң жағынан -ға көбейтіп, мынаны аламыз:
.
Дәл осылай
аламыз.
(12) матрицаны қарастырайық және ол (7), (8) шарттарды қанағаттандыратындығын көрсетейік, яғни псевдокері болатыдығын.
Белгілеу енгізейік:
Онда (1) және (12) қолданып мынаны аламыз:
Мұндағы
Енді берілген матрицасы үшін екі әртүрлі 
және 
псевдокері матрицаның болмайтындығын дәлелдейік. Расында да:
, 
бұдан
, 
Белгілеу еңгізейік
(13)
Онда келесі теңдіктер орындалады:
, 
Ал бұдан
бұл (13) сәйкес мынаған тепе – тең
.
Осылайша, псевдокері матрицаның жалғыз болатындығы, және 1-теорема да дәлелденді.
1-теорема псевдокері матрицаны матрицасын скелеттік жіктеу бойынша есептеу әдісін береді.
Мысалы 2. (Псевдокері матрица). 1-мысалдағы матрицасы үшін оның 1-мысалда қолданылған скелеттік жіктеуін және (12) қолданып, псевдокері матрицасын табайық.
Біз әрбір матрицасы үшін жалғыз ғана Мур-Пенроуздың псевдокері матрицасы болатындығын дәлелдедік, және де егер матрицасы өзінің (1) скелеттік жіктелуімен берілсе, онда 
(6) түрге ие болады.
матрицасының кейбір қасиеттерін қарастырайық:
Теорема 2. (Мур-Пенроуздың псевдокері матрицасының қасиеттері). Келесі қасиеттер орынды:
1. 
2. 
3. 
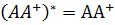, яғни 
матрицасы – эрмитті.
4. 
, яғни 
матрицасы – эрмитті.
5. 
.
6. 
, 
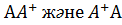матрицалардың рангтары бірдей болады.
7. 
болады, егер жол бойынша толық рангқа ие болса.
8. 
болады, егер баған бойынша толық рангқа ие болса.
9. 
.
ДӘРІС 11, 12
