Айталық 
- өлшемді 
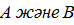матрицалары берілсін және олардың 
көбейтіндісін есептеу керек болсын. Бұны есептеудің классикалық алгоритмі мынадай (программа алгоритмдік Фортран тіліне ұқсас):
Алайда алдымен 
элементтерін нөлге айналдырып алу керек.
«Бұл бағдарламаның жақсы жағы неде?»,- деген сұрақ туындайды. Бұл сұраққа жауап беру оңай емес. Алдымен бізге қандай да бір критерий қажет – айталық осы бағдарламаны орындау уақыты болсын. Алайда уақыт тек компьютердің түріне ғана тәуелді емес.
Бұл жерде бірдене түсіну үшін көптеген бөлшектерді алып тастап, ең негізгісін қалтыру керек. Егер де барлық амалдар тізбектей орындалса, онда жұмыстың орындалу уақытын амалдар санына пропорционал деп есептеуімізге болады. біз қарай жүрейік және тек арифметикалық амалдарды есептейміз. Олардың жалпы санын алгоритмнің арифметикалық күрделілігі деп атаймыз.
Алгоритм –бұл элементар амалдардың соңғы бекітілген жиынтығынан алынған элементар амалдардың тізбегі деп есептейік. Анықтық үшін, айталық бұл төрт арифметикалық амал болсын.
Сонымен, математикалық есеп қойылды. Бұрындары классикалық алгоритм ең жақсы деп есептелген. Қазір байқайтынымыздай ол бұлай емес.
1.8 Виноград әдісі
Классикалық алгоритмді қолданбай матрицаларды көбейткен алғашқылардың бірі (60 жылдардың басында) Виноград болды. Ол келесі тепе – теңдікті қолдануға болатынын көрсетті:
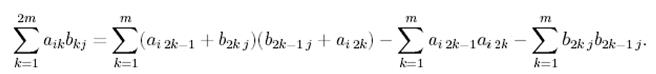
Айталық 
болсын. Барлық 
үшін екінші және үшінші қосындыны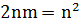 
көбейту және 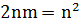қосу амалы арқылы табуға болады. Бірінші қосынды үшін 
көбейту және 
қосу амалы қажет.
Нәтижесінде – бұрынғыдай, 
амал орындалады, бірақ мұнда енді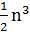 
көбейту және 
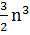қосу амалы болады. көбейту амалы қосуға қарағанда күрделі амал болғандықтан Виноград әдісінің практикалық маңызы бар.
Штрассен әдісі
1965 жылы Штрассен 
- өлшемді матрицаны тек қана 7 көбейтіндінің көмегімен көбейтуді анықтады (классикалық әдісте – 8 көбейтінді қолданылады). Штрассеннің ойлап тапқаны «көп өлшемді матрицалардың» тензорлық рангын есептеу көмегімен алынады.
1.10 
- өлшемді матрицалар үшін рекурсия
7 көбейтіндінің көмегімен есептелетін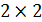 
- өлшемді матрицаларды көбейтуден 
аспайтын амлады қажет ететін 
- өлшемді матрицаларды көбейту әдісіне көшу оңай. 
ұмтылғанда 
ұмтылғандықтан, Штрассен әдісі классикалық әдістен асимптотикалық жақсырақ болып табылады.
Айталық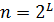 
болсын және 
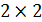матрицаларын - өлшемді блокты матрица түрінде қарастырайық:
Штрассен әдісінде - өлшемді матрицаларды көбейткенде коммутативтілік қолданылмайды. Сондықтан да бұл әдіс - өлшемді блокты матрицаларды көбейту үшін де қолданылады.
Сонымен, 
өлшемді есеп дәл осындай жеті 
өлшемді есепке келтіріледі. Бұл 7 есепті құру үшін және осы 7 есепті шешкеннен кейін қорытынды нәтижені алу үшін ретті блоктарды 18 рет қосу қажет.
Көрсетілген рекурсияны аяғына дейін «бұрмаласақ», соңғы кезеңде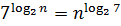 
көбейтуді аламыз. Барлық кезеңдегі қосудың жалпы саны
құрайды. (мұнда 
екендігін ескеру қажет).
Қазіргі кезде Штрассен әдісінен де аса жылдам әдістер ойлап табылған.
ДӘРІС 3,4
