
Файл-функция для этой системы при значениях A 0 = 2 и W = 2 имеет следующий вид:
function dydt = vdp1s(t,y)
dydt = zeros(2,1); dydt(1) = y(2);
dydt(2) = 1*(1-y(1).^2).*y(2)-2*y(1)+2*sin(2*t);
Фазовый портрет показан на рис. 7.
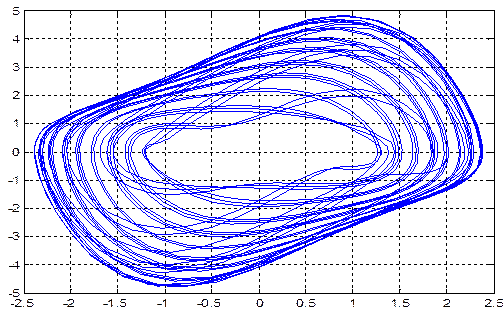
Рис. 7.
Лабораторная работа № 6 – 7
Качественный анализ линейных ДС
ЦЕЛЬ РАБОТЫ
Ознакомление с методами качественного анализа систем ОДУ
Рассмотрим линейную однородную систему с постоянными коэффициентами, которая представляет собой линейную динамическую систему (ЛДС):

| (1) |
Координатную плоскость xOy называют ее фазовой плоскостью (ФП). Через любую точку плоскости проходит одна и только одна фазовая кривая (траектория) (ФТ). В системе (1) возможны три типа ФТ:
· точка,
· замкнутая кривая,
· незамкнутая кривая.
Точка на ФП соответствует стационарному решению (положению равновесия, точке покоя) системы (1), замкнутая кривая периодическому решению, а незамкнутая непериодическому.
Положения равновесия ДС
Положения равновесия системы (1) найдем, решая систему:

| (2) |
Система (1) имеет единственное нулевое положение равновесия, если определитель матрицы системы:
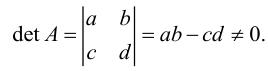
|
Если же det A = 0, то, кроме нулевого положения равновесия, есть и другие, так как в этом случае система (2) имеет бесконечное множество решений.
Качественное поведение ФТ (тип положения равновесия) определяется собственными числами матрицы системы.
Классификация точек покоя
Собственные числа матрицы системы найдем, решая уравнение:

| (3) |
Заметим, что a + d = tr A (след матрицы) и ad – bc = det A.
В СКМ MATLAB определять собственные числа и собственные вектора системы ОДУ удобно с помощью функции eig(A).
Собственные числа l i и собственные векторы ui ≠ 0 квадратной матрицы А удовлетворяют равенствам А ui = l i ui. Функция eig, вызванная с входным аргументом матрицей, находит все собственные числа матрицы и записывает их в выходной аргумент – вектор:
>> A = [2. 3; 3 5];
>> lam = eig(A)
lam =
0.1459
6.8541
>>
Для одновременного вычисления всех собственных векторов и чисел следует вызвать eig с двумя выходными аргументами.
>> [U, Lam] = eig(A);
Первый выходной аргумент и представляет собой матрицу, столбцы которой являются собственными векторами. Для доступа, например, к первому собственному вектору следует использовать индексацию при помощи двоеточия
>> u1=U(:,1)
u1 =
-0.8507
0.5257
Вторым выходным аргументом Lam возвращается диагональная матрица, содержащая собственные числа исходной матрицы.
>> Lam
Lam =
0.1459 0
0 6.8541
Проверьте, правильно ли найдены, например, второе собственное число и соответствующий ему собственный вектор. Воспользуйтесь определением:
>> A*U(:, 2) - Lam(2, 2)*U(:, 2)
ans =
1.0e-015 *
0.4441
-0.8882
Классификация точек покоя в случае, когда det A ≠ 0, приведена в таблице:

Устойчивость точек покоя
Собственные значения матрицы системы (1) однозначно определяют характер устойчивости положений равновесия:

Фазовые портреты





Бесконечное множество точек покоя
Если det A = 0, то система (1) имеет бесконечное множество положений равновесия. При этом возможны три случая:

Во втором случае любая точка покоя устойчива по Ляпунову. В первом же случае только, если l2 < 0.


Направление на фазовой кривой указывает направление движения фазовой точки по кривой при возрастании t.






