Качественный анализ нелинейных ДС
ЦЕЛЬ РАБОТЫ
Ознакомление с методами исследования нелинейных динамических систем и свосвами логистического отображения.
Исследование нелинейных ДС в MATLAB
Рассмотрим ДС представленную системой ОДУ
dx / dt = x 2 + y 2 – 17,
dy / dt = xy + 4.
Для нахождения точек равновесия этой ДС следует решить систему нелинейных уравнений:
x 2 + y 2 – 17 =0,
xy + 4 = 0.
Графическое решение этой системы осуществляется следующей программой (graf_ik.m):
x=[-sqrt(17):0.001:sqrt(17)];
y1=sqrt(17-x.^2);
y2=-sqrt(17-x.^2);
plot(x,y1,x,y2)
hold on
grid on
x1=[-4.5:0.01:-0.7];
z1=-4./x1;
plot(x1,z1,'.')
x1=[0.7:0.01:4.5];
z1=-4./x1;
plot(x1,z1,'.')
hold off

Из анализа графика следует, что имеется четыре значения х при которых функция имеет нулевые значения, это х равные –4, –1, 1 и 4.
Следующая последовательность операторов дает возможность определить соответствующие значения у -ов:
>> x=[-4 -1 1 4];
>> y=-4./x
y =
1 4 -4 -1
Таким образом, имеем следующий набор особых точек:
х у
–4 1
–1 4
1 –4
4 –1
После определения координат точки положения равновесия нужно определить характер точки. Для определения характера точки, разложим функции F 1(x, y) и F 2(x, y) в окрестности точек положения равновесия x 0, y 0, и ограничиваемся первыми тремя членами разложения:

Выписываем коэффициенты при линейных членах и получаем матрицу Якоби или Якобиан:
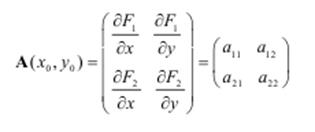
Элементы матрицы Якоби ai,j являются постоянными величинами.
Для определения матрицы Якоби в MATLAB существует функция jacobian. входящая в Symbolic Math Toolbox.
Синтаксис функции
jacobian(f,v)
Чтобы определить характер точек равновесия следует найти собственные числа матрицы Якоби l, решая характеристическое уравнение

где I – единичная матрица или же воспользоваться функцией MATLAB eig.
Для функций f 1 = x 2 + y 2 – 17 и f 2 = x * y + 4 Якобиан вычисляется следующим образом:
>> syms x y
f=[x^2+y^2-17;x*y+4];
v=[x,y];
r=jacobian(f,v)
r =
[ 2*x, 2*y]
[ y, x]
Результат определения Якобиана в особых точках с использованием функции MATLAB subs, собственных значений Якобиана с использованием функции eig(а), а также характер особых точек показан в таблице:
| >> x=-4; >> y=1; >> a=subs(r) a = -8 2 1 -4 >> eig(a) ans = -8.4495 -3.5505 | >> x=-1; >>y=4; >> a=subs(r) a = -2 8 4 -1 >> eig(a) ans = -7.1789 4.1789 | >> x=1; >> y=-4; >> a=subs(r) a = 2 -8 -4 1 >> eig(a) ans = 7.1789 -4.1789 | >> x=4; >> y=-1; >> a=subs(r) a = 8 -2 -1 4 >> eig(a) ans = 8.4495 3.5505 |
| Устойчивый узел | Седло | Седло | Неустойчивый узел |
На следующем рисунке показаны некоторые траектории, соответствующие решениям вышеприведенной системы.
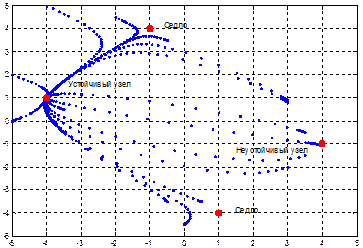
Логистическое отображение
(отображение Ферхюльста)






