Совершать полные вращения
Предположим, что мы хотим с точностью до 0.001 найти наименьшее значение начальной скорости, которая требуется, чтобы заставить маятник, начинающий движение из своего исходного положения, выполнить полное вращение один раз. Будет полезно показать решения, которые соответствуют нескольким различным начальным скоростям на одном графике.
Сначала мы рассмотрим целые значения скорости в промежутке от 5 до 10.
>> hold on
>> for а = 5:10
[t, xa] = ode45(g, [0:0.01:20], [0 а]);
plot(xa(:, 1), xa(:, 2))
end
>> hold off

Рис. 4.
Начальные скорости 5, 6 и 7 не являются достаточно большими (рис. 4), чтобы увеличить угол более π, но начальные скорости 8, 9 и 10 достаточны, чтобы заставить маятник совершать полный оборот. Посмотрим, что происходит на промежутке между 7 и 8.
Второй шаг
>> hold on
>> for а = 7.0:0.2:8.0
[t, ха] = ode45(g, [0:0.01:20], [0 а]);
plot(xa(:, 1), xa(:, 2))
end
>> hold off

Рис. 5.
Можно заметить (рис. 6), что ответ находится где-то между 7.2 и 7.4. Давайте выполним еще одно уточнение.
Третий шаг
>> hold on
>> for а = 7.2:0.05:7.4
[t, ха] = ode45(g, [0:0.01:20], [0 а]);
plot(xa(:, 1), ха(:, 2))
end
» hold off

Рис. 6.
Следует сделать вывод, что наименьшая необходимая скорость с точностью 0,01 находится где-то между 7.25 и 7.3 (рис. 7 и 8).
Четвертый шаг
for a = 7.25:0.01:7.3
[t, xa] = ode45(g, [0:0.01:20], [0 a]);
plot(xa(:, 1), xa(:, 2))
end

Рис. 7.
Для более точного анализа увеличим область графика, где происходит смена режима колебания.

Рис. 8.
Видно, что наименьшая необходимая скорость находится где-то между 7.29 и 7.3.
Следует продолжить нахождение более точного значения скорости смены режима колебания.
Динамика осциллятора Ван дер Поля при w2 = 2 и c = 1
Предельный цикл – устойчивый режим периодических колебаний в нелинейных системах после завершения переходных процессов
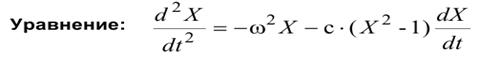

Файл-функция, для этих параметров, имеет следующий вид (см. Андреев 2013, с. 117):
function dydt = vdp1(t,y)
dydt = zeros(2,1); dydt(1) = y(2);
dydt(2) = 1*(1-y(1).^2).*y(2)-2*y(1);
При начальном положении на предельном цикле (х0 = 2, v0= 0) вызов файл-функции имеет следующий вид:
[t,y] = ode23(@vdp1,[0 25],[2;0]);
Следующий оператор дает возможность получить зависимость х и v от времени
plot(t,y(:,1),t,y(:,2)), grid on
Результат показан на рис. 1.

Рис. 1.
Следующий оператор дает возможность получить фазовый портрет системы (рис. 2):
plot(y(:,1),y(:,2)), grid on

Рис. 2.
Если взять начальные данные вне цикла (х0 = -0.5, v0= 5) вызов файл-функции имеет следующий вид:
[t,y] = ode23(@vdp1,[0 25],[-0.5;5]);
Результат показан на рис. 3.

Рис. 3.
Фазовый портрет показан на рис. 4.
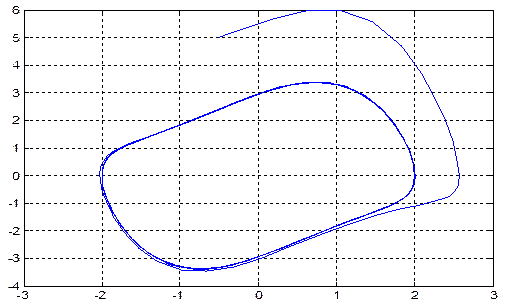
Рис. 4.
Если взять начальные данные внутри цикла (х0 = -0.05, v0= -0.05) вызов файл-функции имеет следующий вид:
[t,y] = ode23(@vdp1,[0 50],[-0.05; -0.05]);
Результат показан на рис. 5.

Рис. 5.
Фазовый портрет показан на рис. 6.
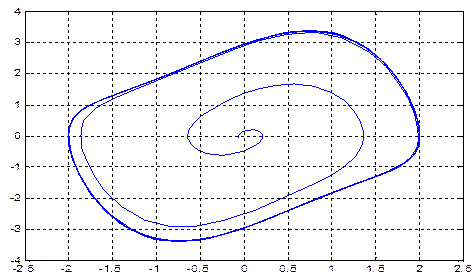
Рис. 6.






