Запомните 
| Умножение | двухдесятичных | дробей | выполняется так: | |||
| 1) | числа | перемножаются | без | учета | запятых. | |
2) запятая в произведении ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.
Например:
1,1 • 0,2 = 0,22; 1,1 • 1,1 = 1,21; 2,2 • 0,1 = 0,22.
Примеры умножения десятичных дробей в столбик:
Запомните
При умножении любой десятичной дроби на10,100,1000и т.д.запятая вдесятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.
Примеры:
70,1 · 10 = 701
0,023 · 100 = 2,3
5,6 · 1 000 = 5 600
Запомните
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001; и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.
Считаем и ноль целых!
Примеры:
12 · 0,1 = 1,2
0,05 · 0,1 = 0,005
1,256 · 0,01 = 0,012 56
БИЛЕТ №24
Деление десятичных дробей.
Для деления десятичной дроби на натуральное число пользуемся следующими правилами.
Запомните
1. Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
2. Ставим в частном запятую, когда заканчивается деление целой части делимого.
Если целая часть делимого меньше делителя, то в частном ставим 0 целых.
Пример:
0,806: 31 =
Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части.
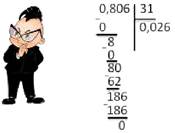
Не забываем записывать ответ в пример:
0,806: 31 = 0,026
Запомните
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Примеры:
310,1: 10 = 31,01
27,56: 100 = 0,2756
0,75: 10 = 0,075
Запомните
При делении на десятичную дробь, сначала переносим запятую в делимом
и делителе вправо на столько знаков, сколько их после запятой в делителе. А затем выполняем деление на натуральное число.
Например:
543,96: 0,3 = 5439,6: 3 = 1813,2;
237: 0,03 = 23700: 3 = 7900
БИЛЕТ№25
Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде
Десятичной.
Десятичную дробь представляют в виде обыкновенной дроби, записав
ее со знаменателем. При этом число целых искомой обыкновенной дроби равно числу целых десятичной дроби. В числителе искомой
дроби пишем цифры, стоящие после запятой (десятичные знаки), а в знаменателе записываем 1 с количеством нулей, которое равно
количеству десятичных знаков. Далее, если возможно, производят сокращение дроби.
Если десятичные знаки начинаются нулями, их в числитель обыкновенной дроби писать не нужно.
Запомните
Обыкновенную дробь можно перевести в конечную десятичную дробь, если
её знаменатель раскладывается только на множители 2 и 5, которые могут повторятся.
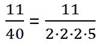
Примеры:
Дробь 11/40 можно преобразовать в конечную десятичную. Её знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
Не все обыкновенные дроби можно представить в виде конечной десятичной дроби.
Например, если делить 2 на 3, то сначала получим ноль целых, потом шесть десятых, а затем при делении всё время будет повторяться остаток 2, а в частном — цифра 6. Такое деление закончить без остатка невозможно и поэтому дробь 2/3 нельзя представить в виде конечной десятичной дроби.
Запомните
Если в записи десятичной дроби одна цифра или группа цифр начинают
повторяться бесконечно много раз, такую дробь называют периодической дробью.
В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.
Вместо 0,666... пишут 0,(6) и читают «ноль целых и шесть в периоде».
