СПРАВОЧНЫЙ МАТЕРИАЛ
ПО ПОДГОТОВКЕ К ОТВЕТУ НА ТЕОРЕТИЧЕСКИЙ ВОПРОС
ПЕРЕВОДНОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ В 6-ом КЛАССЕ
БИЛЕТ №1
Натуральные числа. Сложение натуральных чисел. Законы сложения.
Запомните 
Натуральные числа —это числа,начиная с1,получаемые при счете предметов.
1,2,3,4,5...
Наименьшее натуральное число —1.
Наибольшего натурального числа не существует.
При счёте число ноль не используется, поэтому ноль не считается натуральным числом. Всего цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью этих цифр можно записать любое
натуральное число.
Переместительный закон сложения
Запомните
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так: a + b = b + a
В этом равенстве буквы a и b могут принимать любые натуральные значения и значение 0.
Пример:
90 + 20 = 20 + 90 = 110
Сочетательный закон сложения
Запомните
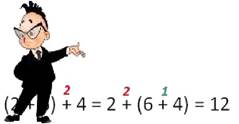
Чтобы к сумме двух чисел прибавить третье число можно к первому числу
прибавить сумму второго и третьего числа.
В буквенном виде:
(a + b) + c = a + (b + c)
Например:
6 + 4 + (3 + 2) = 6 + (4 + 3) + 2 = (6 + 4) + 3 + 2 = 15
Обратите внимание, этот закон действует только, если все действия в примере
сложение!
Запомните
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
БИЛЕТ №2
Умножение. Законы умножения.
Свойства умножения
Переместительное свойство умножения
Запомните 
От перестановки множителей произведение не меняется.
a · b = b · a
Пример:
11 · 4 = 4 · 11 = 44
Сочетательное свойство умножения
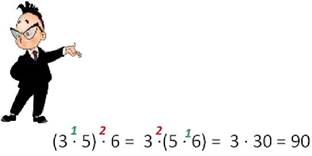Запомните
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
a · (b · c) = (a · b) · c
Свойство нуля при умножении
Запомните
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
a · 0 = 0
0 · a · b · c = 0
Если в произведении один из множитель равен нулю, то само произведение будет равно нулю.
a · 0 = 0
0 · a · b · c = 0
Распределительное свойство умножения относительно сложения
Запомните
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.
(a + b) · c = a · c + b · c
Например: 8 · (6 + 5) = 8 · 6 + 8 · 5 = 48 + 40 = 88
Распределительное свойство умножения относительно вычитания
Запомните
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так: (a − b) · c = a · c − b · c
Например: 8 · (6 - 5) = 8 · 6 - 8 · 5 = 48 - 40 = 8
Запомните
При умножение любого числа на 1 получается это же число.
a · 1 = a
Например: 18 · 1=18
БИЛЕТ №3
Степень с натуральным показателем
Запомните
Степенью натурального числа a называют произведение нескольких множителей,
каждый из которых равен а.
Например:
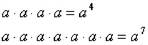
Квадрат числа а
Произведение a умножить на a называют второй степенью или квадратом числа a. Запомните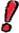 
Например:
4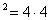 
Квадраты первых десяти натуральных чисел вы легко вспомните
с помощью таблицы умножения:
И ие квадраты чисел также можете легко найти. Куб числа а
Запомните
