Запомните 

Чтобы сложить отрицательные числа,нужно сложить их модули и
поставить перед суммой знак минус.
Пример. (−3,2) + (−4,3) = − (3,2 + 4,3) = −7,5
Сложение чисел с разными знаками
Если числа имеют разные знаки, то действуем несколько по-иному, чем при сложении чисел с одинаковыми знаками.
· Отбрасываем знаки перед числами, то есть берём их модули.
· Из большего модуля вычитаем меньший.
· Перед разностью ставим тот знак, который был у числа с большим модулем.
Пример сложения отрицательного и положительного числа.
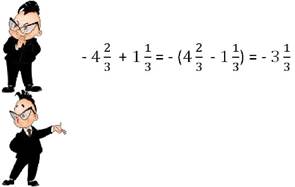
0,3 + (−0,8) = −(0,8 − 0,3) = −0,5
Пример сложения смешанных чисел.
Запомните 
Чтобы сложить числа с разными знаками надо:
· из большего модуля вычесть меньший модуль;
· перед полученной разностью поставить знак числа, имеющего больший модуль.
БИЛЕТ №19
Умножение и деление положительных и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Запомните 

Чтобы умножить два числа с одинаковыми знаками надо:
· перемножить модули чисел;
· перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).
Примеры умножения отрицательных и положительных чисел.
(−3) · (−6) = + 18 = 18
2 · 3 = 6
Умножение чисел с разными знаками
 Запомните
Запомните 
Чтобы умножить два числа с разными знаками, надо:
· перемножить модули чисел;
· перед полученным произведением поставить знак «−».
Примеры умножения отрицательных и положительных чисел.
· (−0,3) · 0,5 = −0,15
· 1,2 · (−7) = −8,4
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с
правилом раскрытия скобок.

| Запомните | + · (+) =+ | + · (−) =− | ||||
| Минус на минус даёт плюс, | ||||||
| − · (−) =+ | − · (+) =− | |||||
| Плюс на минус даёт минус. | ||||||
| В «длинных» примерах, в которых есть | только действие | |||||

умножение, знак произведения можно определять по количеству отрицательных множителей. При чётном числе отрицательных множителей результат будет положительным, а при
нечётном количестве — отрицательным.
Пример.
(−6) · (−3) · (−4) · (−2) · 12 · (−1) =
В примере пять отрицательных множителей. Значит, знак результата будет «минус». Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 · 3 · 4 · 2 · 12 · 1 = 1728
Конечный результат умножения исходных чисел будет:
(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728
Правила деления отрицательных чисел

Запомните 
Чтобы разделить два отрицательных числа надо:
· модуль делимого разделить на модуль делителя;
· перед результатом поставить знак «+».
Примеры деления чисел с одинаковыми знаками:
(−9): (−3) = + 3
Запомните 

Чтобы разделить два числа с разными знаками, надо:
· модуль делимого разделить на модуль делителя;
· перед результатом поставить знак «−».
Примеры деления чисел с разными знаками:
(−5): 2 = −2,5
28: (−2) = −14
Для определения знака частного можно также пользоваться следующей таблицей.






+: (+) =+ +: (−) =−

−: (−) =+ −: (+) =−
БИЛЕТ№20
 Раскрытие скобок и заключение в скобки
Раскрытие скобок и заключение в скобки
Выражение а+(b+с) можно записать без скобок:
а +(b+с) = а + b + с
Эту операцию называют
раскрытием скобок.
Пример 1. Раскроем скобки в
выражении а + (- b + с).
Решение. а + (- b + с) = а + ((-b) + с) = а + (-b) + с = а - b + с.
Запомните 
Если перед скобками стоит знак " + ",то можно опустить скобки и этот знак" +", сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком " + ".
- 2,87 + (2,87 - 7,639) = - 2,87 + 2,87 - 7,639 = 0 - 7,639 = - 7,639.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
Значит: -(а + b) = -a - b.
Запомните 
Чтобы раскрыть скобки, перед которыми стоит знак " - ",надо заменить этотзнак на " + ", поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Значит:
9,36 - (9,36 - 5,48) = 9,36 + (-9,36 + 5,48) = 9,36 - 9,36 + 5,48 = 0 + 5,48 = 5,48.
Запомните 
Если сумма заключается в скобки, перед которыми стоит знак «+», то знаки
слагаемых, заключённых в скобки, оставляют без изменения.
-а+b-с= +(-а+b-с)

Примеры.
1) -4+9-5= +(-4+9-5)
2) -96+22= +(-96+22)
3) 56-28+23-4= +(56-28+23-4)
Запомните 
Если сумма заключается в скобки, перед которыми стоит знак «-», то знаки слагаемых, заключённых в скобки, меняют на противоположные.
а-b+с-d= -(-a+b-c+d)
Примеры.
1) 123-25+37= -(-123+25-37)
2) -56+38-49= -(56-38+49)
3) 35-77+65= -(-35+77-65)
БИЛЕТ№21







