Переход из состояния x в состояние может осуществиться в любой момент времени. Обозначим Xi(t) – случайное событие, система в момент времени t находится в состоянии i.
P(Xi(t))=pi(t) – функция времени, а не этапа, переходные вероятности.
Введем обозначения:
вероятность того, что система, находившаяся в момент t в состоянии xi за временной промежуток [t,t+дельта t). Эта вероятность может быть равна нулю в одном из трех случаев:
1) в момент времени t система находилась в состоянии xi и находилась в нем на протяжении всего рассматриваемого временного промежутка;
2) в момент t система находилась в xi, но за рассматриваемый промежуток перешла в другое состояние, отличное от xj;
3) В момент времени t система не находилась в состоянии xi.
Во всех других случаях вероятность строго положительна, однако стремится к нулю при дельта t стремящемся к нулю.
Предел отношения 
Из определения следует, что плотности вероятностей перехода могут принимать любое неотрицательное значение в том числе и больше 1. 
Граф состояний системы, дуги которого нагружены плотностями переходных вероятностей называется размеченным графом системы.
Из определения следует асимптотическая формула: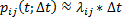 
Вероятности состояний системы могут быть найдены как решения нормальной системы дифференциальных уравнений следующего вида:
i= 
Первое правило составления системы Колмогорова:
1. Для того, чтобы составить i-е уравнение системы в левой его части следует записать производную 
. Справа произведение суммы плотностей вероятностей дуг, исходящих из i-го состояния на вероятность этого состояния, взятое со знаком минус и добавить к нему сумму парных произведений плотностей вероятностей дуг, входящих в i-е состояние и вероятностей состояний, из которых осуществляется переход в xi.
2. Второе правило по матрице плотности. Справа – сумма элементов i-й строки матрицы 
умноженная на вероятность i-го состояния и это произведение берется со знаком минус. Со знаком плюс, каждый элемент i-го столбца умножается на вероятность состояния одноименного номеру строки и эти произведения берутся со знаком плюс. Решение системы Колмогорова находится методами теории обыкновенных дифференциальных уравнений.
Нормальная система диф уравнений имеет вид: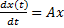 
Решением системы называется n-ка функций, которая при подстановке в систему обращает каждое ее уравнение в верное числовое равенство.
Общим решением x(t) называется вектор функции, зависящий от аргумента t и n произвольных состояний, которая является решением системы при любом конкретном выборе значения произвольных состояний.
