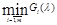Обобщенный критерий Гурвица для безопасной и опасной ситуаций. 3
Понятие ситуации риска, основные постулаты риск-менеджмента, формализация ситуации риска, принципы доминирования. 4
Меры риска, масштабные и вероятностные. 5
7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода. 6
8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску. 7
Понятие кривой безразличия. Три типа кривых безразличия. 7
Понятие идеального эксперимента, обоснование его целесообразности. 8
Понятие неидеального эксперимента, алгоритм обоснования его целесообразности. 8
Смешанные стратегии как инструмент уменьшения риска. 8
Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности. 9
Интенсивность несклонности к риску, премия за риск (подход Марковица). 11
Формула Эрроу-Пратта. 11
Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения. 12
Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана. 13
Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена. 13
19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения. 14
20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора. 15
Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов). 15
Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления. 16
Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток. 17
Вероятностные характеристики простейшего потока. 17
Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс. 18
Процессы гибели и размножения, финальные вероятности состояний. 19
27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний. 20
Системы массового обслуживания, их основные компоненты и характеристики функционирования. 20
Многоканальные системы массового обслуживания с отказами. 21
Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди. 22
1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия.
Математически ЗПР при многих критериях в строго детерминированной ситуации задается картежом: <A, (f1, f2, …, fm)>; fi – функция, количественно характеризующая i-тый критерий. 
Для каждого локального критерия Ki и выражающей его функции fi рассмотрим множество оценок по этому критерию: 
Y – множество векторных оценок А, и на этом множестве вводится бинарное отношение доминирования по Парето. Говорят, что векторная оценка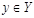 
доминирует по Парето 
:
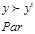если 
и существует такой i: 
Множество недоминируемых по Парето векторных оценок составляет Парето оптимальное множество или границу Парето: Отношение доминирования по Парето переносится непосредственно на сравниваемые А. Говорят, что Аа из множества А доминирует А а’ из множества А по Парето, если векторная оценка Аа доминирует по Парето векторную оценку Аа’: 
Недостаток критерия Парето состоит в том, что он незначительно сокращает множество возможных исходов и как следствие допустимых альтернатив.
Методы сокращения/суждения Парето – оптимального множества
1.Задание пороговых значений критериев. Исходная оптимальная задача заменяется задачей поиска А 
, удовлетворяющей системе неравенств:
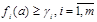; γi – пороговое значение соответственного критерия, которое не может быть ухудшено. 
«-» не позволяет отыскать единственное решение, а лишь отбирает приемлемые варианты, оценка которой по всем критериям превосходит установленные пороги.
2.Субоптимизация, сокращение границы Парето. Один из критериев, например, 1-ый, объявляется главным, а остальные переводятся в разряд ограничений: 
3. Лексикографическая оптимизация. Предполагался, что все локальные критерии ранжированы по их значимости (упорядочены). Сначала рассматривается задача оптимизации по наибольшему значимому критерию. Если А стремится к мах значению и эта А единственна, то она и принимается в качестве оптимальной. Если таких А несколько, то на множестве, составленном из них, рассматривается задача максимизации. Если А конечное число, то за конечное число шагов будет выбрана опт. А.
Методы построения обобщенного критерия, свертки критериев – процедура, которая агрегирует набор оценок по заданным локальным критериям в итоговую числовую оценку, выражающую совокупную ценность этого набора для ЛПР. Обобщенный критерий задаётся функцией, сохраняющей исходную упорядоченность альтернатив (лучшим альтернативам соответствует большие значения обобщенного критерия). Задание обобщенного критерия превращает многокритериальную задачу в задачу одномерной оптимизации. Обобщенный Критерий не позволяет в полной мере использовать всю инфу, которая имеется в векторной оценке. Частные критерии оценки проекта можно разделить на 2 группы: критерии отражающие результат и критерии связанные с затратами. Предположим, удалось построить обобщенный показатель рез-та R и обобщенный показатель затрат С. Обобщенной оценкой проекта может служить показатель эффективности: 
. Обобщенные критерии обычно строятся в форме свёрток:
1)максимин свёртка: 
(подтянем худшего). На практике чаще пользуются нормированной свёрткой, когда задаются эталонные значения 
для каждого критерия и отклонения от этих эталонов минимизируется 
2)Мультипликативная свёртка 
. Используется когда все локальные критерии критически важны для ЛПР и обращение в 0 хотя бы одного из них лишает смысла весь результат.
3)Аддитивная свёртка 
2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора.
Метод предназначен для ранжирования (упорядочения) объектов в применении к следующей задаче: имеется конечное множество объектов {p1, p2, …, pm}, требуется ранжировать их, приписав каждому из объектов весовой коэффициент, который в совокупности образует вектор весовых коэффициентов или вектор приоритетов.
Предположим, что весовые коэффициенты известны, составим из них матрицу отношений A=(aij).
Матрица А обладает тем свойством, что вектор приоритетов является собственным вектором этой матрицы отвечающей собственному числу (λ).
Еe собственным вектором называется нетривиальный вектор x удовлетворяющий матричному уравнению AX=λX.
На практике вектор приоритетов находится построением и анализом матрицы парных сравнений, которая в определенной степени заменяет матрицу отношений (А).
Шкала превосходства
| Количественная оценка | Содержательное описание степени превосходства |
| Равная важность | |
| Умеренное превосходство | |
| Существенное превосходство | |
| Значительное превосходство | |
| Подавляющее превосходство | |
| 2, 4, 6, 8 | Промежуточные значения между соседними оценками |
| Обратные величины |
По своему построению матрица парных сравнений является положительной и обратно симметричной. Для того, чтобы матрица парных сравнений выражала непротиворечивые суждения ЛПР она должна дополнительно удовлетворять условию согласованности.
Формальным обоснованием требования согласованности является следующее утверждение: если матрица А является согласованной, то существуют положительные числа альфа, что aij=αi/αj.
Матрица парных сравнений, отражающая субъективное мнение ЛПР, может быть несогласованной. Важно лишь, чтобы степень несогласованности не превышала какой-то предельный уровень.
Измерение степени согласованности базируется на двух фактах из линейной алгебры.
1.Если в положительной матрице А выполняется аii = 1, то 
. Из этого следует, что в идеально согласованной матрице 
, остальные собственные числа = 0.
2.Собственный числа являются непрерывными функциями от элементов матрицы.
Из этих утверждений следует что если матрица парных сравнений мало отличается от идеально согласованной матрицы отношений, то λmax матрицы парных сравнений мало отличается от m. Для количественной оценки возможных отклонений вводится коэффициент согласованности
RI - стохастический индекс согласованности
CI – это индекс согласованности
CR<=0,1 – согласованность считается приемлемой, в противном случае нет.
Собственное число и собственный вектор матрицы А находятся приближенно. Для этого на ряду с матрицей парных сравнений А рассматривается нормализованная матрица N того же порядка, состоящая из чисел nij, полученные делением кажд эл-та столбца на сумму эл-тов кажд столбца.
Если все столбцы матрицы N одинаковы, значит матрица А является идеально согласованной и любой столбец матрицы N может быть выбран в качестве вектора приоритета. В противном случае элементы матрицы А усредняются по строкам, т.е. сумма элементов в каждой строке делится на число элементов в этой строке и это число принимается за приоритет этого объекта 
.В совокупности и образуют вектор приоритета.
Для проверки непротиворечивости полученного результата необходимо найти λmax и проверить согласованность. По определению λmax находится из решения матричного уравнения, которое равносильно линейной система, где i-е уравнение имеет вид:
(по определению)
Просуммируем эти уравнения.
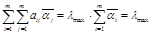(сумма равна 1)
Для того чтобы найти λmax достаточно матрицу парных сравнений А умножить на приближенный вектор приоритетов и получившиеся произведения сложить (в формуле ниже 
– вектор).
3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица.
1.Критерии Лапласа (недостаточного обоснования). Все состояния природы считаются равновероятными, и каждое из них реализуется с вероятностью 1/n. Каждая стратегия ЛПР Ai оценивается средней величиной: 
. Если матрица А – матрица выигрышей, то оптимальная стратегия, доставляющая максимум 
, проигрыш – минимум 
2.Критерий Вальда (пессимистический, по наихудшему варианту): Оценивает каждую стратегию ЛПР по наихудшему варианту развития событий.А – матрица выигрышей 
; А – матрица проигрышей 
.
3.Критерий Сэвиджа. Применение этого критерия требует предварительного построения матрицы рисков Rij = (rij). А – матрица выигрышей 
- максимальный элемент j – столбца 
. А – матрица проигрышей 
- минимальный элемент j – столбца 
. Другое название – матрица сожалений (об упущенной выгоде). В независимости от того, какой была исходная матрица (выигрыша/проигрыша), матрица риска всегда является матрицей потерь (проигрыша). Решение по матрице рисков находится в силу минимаксного варианта критерия Вальда: каждая стратегия ЛПР оценивается максимальным риском, ей присущим, а затем этот максимальный риск минимизируется.
4. Критерий Гурвица.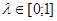 
-показатель оптимизма ЛПР. Каждая стратегия оценивается числом Gi(λ), построение которого зависит от типа матрицы:
А – матрица выигрышей 
. Обобщенная оценка стратегии 
.
А – матрица проигрышей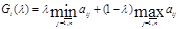 
. Обобщенная оценка стратегии 
