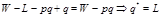Функция полезности — функция, показывающая убывание предельной полезности блага с ростом его количества
Алгоритм построения функции полезности:
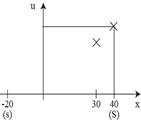
1.из некоторых соображений ограничиваем интервал рассматриваемых денежных сумм, приняв в качестве этого интервала [s, S] ([-20; 40]);
2.вводим произвольную, но логическую шкалу полезности (логич в том смысле, что большим ден суммам отвеч большее значение полезности): U(s) = 0; U(S) = 100 (ед. полез-ти).
3.для каждого значения 
рассчитывают нейтральную вероятность p0 такую, что обладание денежной суммой в x ед. равносильно участию в лотерее, где вероятность выиграть S равна p0, а s руб. – (1 – p0).
0,9 – много; 0,8 – мало; 0,85 – мало; p0 = 0,875 – хватит.
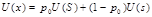; x0,5 – середина
Виды отношений к риску. Простой лотереей называется лотерея с двумя исходами L{x1, x2; p}, x1 > x2. p – вероятность получить выигрыш x1. (1 – p) – вероятность получить выигрыш x2.
Ожидаемый выигрыш в простой лотерее: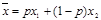 
. Опр. Гарантированным эквивалентом простой лотереи наз ден сумма В, обладание которой для ЛПР равносильно участию в лотерее. Из сопоставления ожидаемого выигрыша 
и гарантированного эквивалента В выявляется склонность ЛПР к риску: 1.если ожидаемый выигрыш 
, значит ЛПР склонен к риску; 2.если ожидаемый выигрыш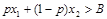 
, значит ЛПР не склонен к риску; 3.если ожидаемый выигрыш 
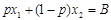, значит ЛПР нейтрален к риску.
Введем полезность простой лотереи аналогично тому, как это делалось в алгоритме построения функции полезности:
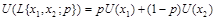
Имея в виду, что шкала полез-ти явл произв-ой, но логич (большим ден. суммам отвеч больш. Знач полез-ти), применим функ-ию полез-ти к соотн 1-3:
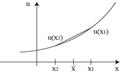
1. 
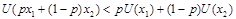. График функции полезности является выпуклым вниз
2. 
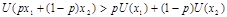. ЛПР не склонен к риску
3. 
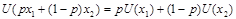. ЛПР нейтрален к риску
1.ЛПР склонен к риску 
| 2.ЛПР не склонен к риску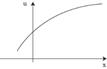 
|
3.ЛПР нейтрален к риску
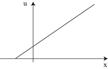
| 4.“Экстремист” – боится долговых обязательств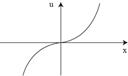 
|
5.“Зануда” – индифферентен, ему все равно
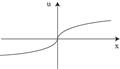7.Обладание малым очень радует, чем больше долг, тем мрачнее
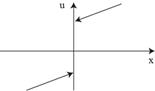
| 6.Типичный человек: сначала рискует, после достижения определенной суммы не рискует, но готов рискнуть малой суммой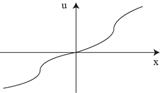 
|
8.Настроение человека, у которого есть долг (имеет долг в а руб.)
|
Применение функции полезности в страховании:
Пусть финансовое состояние ЛПР оценивается W. Предполагается, что можно оценить вероятность р, с которой ЛПР теряет часть своего богатства в размере L. ЛПР может купить страховой полис, в соответствии с которым, ему возмещается ущерб в размере q. Плата за страхование составляет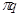 
, где 
- доля страховки в объеме нанесенного ущерба. Определить оптимальное страховое возмещение q*, при которой ожидаемая полезность ЛПР будет наибольшей.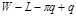 
- наступление страхового случая. 
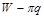- не наступление страхового случая
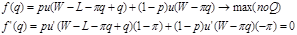
При не наступлении (1-р)= 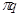. Средний ожидаемый доход: 
В условиях конкуренции страховая компания получает выгоды за счет взносов.
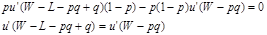
В предп-ии, что ф-ия полез-ти явл строго монотонной, а ее график – строго выпукл вверх, первая произв-я функции полез-ти также облад св-ом монот-ти, и потому из рав-ва произ-ых можно сделать вывод о рав-ве их аргум-ов.
Последнее означает, что из равенства производных следует равенство их аргументов. 
