Если ЛПР не склонен к риску, график его функции полезности является выпукл вверх. В случае, если существ вторая произвольная от функции полезности, это равносильно тому, что 
<0. Однако непосредственно использовать 
для количественно оценки несклонности к риску нельзя. Шкала полезности является хоть и логической, но произвольной в том смысле, что линейное преобразование функции полезности, сохраняя упорядочение альтернатив, меняет значение функции и ее производных.
Необходимо, чтобы мера несклонности к риску обладала следующими условиями: 1.Показывала субъективное отношение к риску.
2. Была инвариантна относительно линейного преобразования функции полезности, т.е. оценок для функции u(x), v(x)=αu(x)+β, α>0.
В то же время отношение 1 и 2 произвольной не меняется при линейной трансформации и именно оно может быть использовано как количественная мера интенсивности несклонности к риску. Альтернативный подход состоит в том, что интенсивность несклонности к риску измеряется с помощью индивид-ой премии за риск. Пусть ЛПР обладает гарантированным доходом W0 одновременно с простой лотереей 
. Свяжем с простой лотереей случайную величину выигрыша Х, ее математическое ожидание 
. Введем полезность одновременного обложения простой лотереи и гарантированного дохода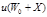 
. Вместе с Х эта полезность является случайной величиной и говорить о ее оптимизации можно в смысле ее математического ожидания: 
Если ЛПР не склонен к риску, он готов уступить участие в простой лотерее за денежную сумму, меньше, чем 
на некоторую величину 
которая называется премией за риск. Величина премии за риск определяется из условия: 
.Абсолютное большинство функций полезности является монотонно возрастающими и потому имеют обратные. Берем функцию 
от обеих частей последнего равенства 
.
Сама формула называется формулой Марковица. Полученная фор-ла выраж премию за риск через субъект особ-ти ЛПР и хар-ки самой лотереи, заключается в величине Х.
Формула Эрроу-Пратта.
Величина премии за риск определяется из условия:
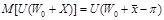
- безрисковый эквивалент одновременного обладания простой лотереей и гарантированным доходом. (формула Марковица). Величину премии за риск желательно разделить на составляющие, одна из которых выражает субъективные особенности ЛПР, а другая характеристики самой лотереи., заключ. в случ. величине Х. 
.
Раскладываем обе части этого равенства по ф-ле Тейлора в окрестности точки 
:
Где 
. (
) = DX.
приравниваем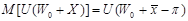 
. Получаем:
. где DX – хар-ка L (лотереи);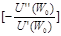 
- коэффициент несклонности к риску.
- формула Эрроу-Пратта.
