+ начало 5 вопроса
Мера риска – это абсолютная (относительная) величина или вероятностный показатель возможных отклонений результатов хозяйственной деятельности в заданных условиях в течение определенного времени. Абсолютная величина результатов выражается в денежной форме и характеризует их среднее значение или разброс относительно среднего значения. Относительная величина выражается в дольном или процентном отношении к ожидаемым результатам. В качестве вероятностной меры риска обычно используют закон распределения случайной величины, устанавливающий связь между ее возможными значениями и вероятностями их реализации. Рассматривая риск с точки зрения его оценки, необходимо решить следующую задачу:
1.выделить и формализованно описать все возможные варианты окружающей обстановки (состояния природы);
2. рассчитать или оценить вероятности реализации этих вариантов;
3.количественно оценить каждую ситуацию принятия решения, которая на содержательном уровне понимается как пара, составленная из стратегии ЛПР и состояния окружающей среды.
Вероятности реализации отдельных вариантов обстановки рассчитываются количественными методами, либо оцениваются на качественном уровне. Количественные методы делятся на 3 группы: 1.прямые вероятностные методы m/n (количество случайных наблюдений / общее число); 2.приближенные методы (возвращение кредита); 3.косвенный (метод аналогий).
Информация, получаемая при решении перечисленных задач, обобщенно представляется законом распределения случайной величины, который для случайной величины дискретного типа представляет собой ряд распределения:
| Возможные значения случайной величины xj | x1 | x2 | … | xn | x1<x2<…<xn |
| Вероятности их реализации pj | p1 | p2 | … | pn | 
|
| Кумулятивная функция (распределения) | F(x1) | F(x2) | … | F(xn) | F(x) = 0, x <= x1 F(x) = 1, x > xn |
Fx(x) = P(X < x). Для случайной величины дискретного типа: функция распределения 
.
7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода.
Критерий ожидаемого значения. Каждая стратегия ЛПР оценивается по среднему ожидаемому значению: Ai: 
. Если А – матрица выигрышей, то стратегия находится из условия максимизации: 
. Если А – матрица проигрышей, то стратегия находится из условия минимизации: 
.
Критерий минимальной вариации. Каждая альтернатива Ai оценивается присущим ей риском, измеренным стандартным отклонением σi или коэффициентом вариации Vi. Оптимальной считается та альтернатива, для которой эта оценка является наименьшей. 
; 
.
Критерий предельного уровня. Исходя из некоторых соображений, устанавливается предельное значение случайной величины, характеризующее качество решения. Любая альтернатива, превышающая установленный порог, считается оптимальной. Критерий предельного уровня не дает единственного оптимального решения. Скорее он соответствует приемлемому способу действия – это недостаток. Достоинство: применение критерия не требует точной информации о законе распределения случайной величины. При назначенном предельном уровне достаточно приближенной информации о ситуации принятия решения.
4. Критерий наиболее вероятного исхода. Каждая случайная величина, описывающая исход применения той или иной стратегии, заменяется детерминированной величиной. За эту величину принимается то значение случайной величины, которое достигается с наибольшей вероятностью: Ai:
| ai1 | ai2 | … | ain |
| p1 | p2 | … | pn |
.
(ai с волной)
Главный недостаток: этот критерий нельзя применять в том случае, когда закон распределения случайной величины не имеет четко выраженного максимума.
8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску.
Пусть критерий X показывает выигрыш ЛПР. Оптимальной стратегией ЛПР считается та, которая доставляет максимум функции: 
. λ – числовой параметр, характеризующий несклонность ЛПР к риску. Оценить приемлемый для ЛПР уровень λ можно с помощью неравенства Чебышева:
(вероятность отклонения от математического ожидания больше, чем на а).
Применяя обобщенный критерий, ЛПР оценивает каждую свою стратегию числом: 
. Ситуация риска, т.е. то, что истинное значение случайной величины X окажется меньше расчетной оценки значит, что: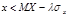 
(подводим под неравенство Чебышева); 
. Если λ =3 => p = 90%. Если количественный показатель X представляет собой проигрыш ЛПР, то оптимальной считается та стратегия, которая доставляет минимум функции: 
