Эквивалентность ставок на разных периодах

Интерес так же представляют случаи, когда ставится вопрос о нахождении значений эквивалентных ставок (то есть ставок, приводящих к одинаковым результатам наращения или дисконтирования) для различных по длительности периодов времени на которых действует каждая из ставок.

Примером может служить следующая задача: для операции наращения по годовой ставке простых процентов i на временном отрезке n_i найти эквивалентную годовую ставку сложных процентов ic на временном отрезке n_ic, где n_i, n_ic для простоты будем считать целыми числами полных лет.

По аналогии с рассмотренным выше, воспользуемся определением эквивалентности ставок и приравняем для каждого периода времени n_i, n_ic коэффициенты наращения по каждой из ставок простой i и сложной i_c. Тогда согласно соотношению (6.1) получим выражение

, (6.4)

из которого легко можно найти значение искомой эквивалентной ставки i_c

(6.5)

Распространяя подобные рассуждения на остальные случаи определения соотношений, выражающих эквивалентность ставок, при различных по длительности сроках t_i = n_i + t _i / T, t_ic = n_ic + t _ic / T, t_d = n_d + t_d / T, t_dc = n_dc + t _dc / T (здесь и далее индексами i_c, i_c, d, d_c будем обозначать временные отрезки n и t, на которых действует соответствующая ставка) полученные результаты также сведем в табл. 6.4 для процессов наращения и табл. 6.5 для процессов дисконтирования.

Таблица 6.4

i =
d =	(1 – (1 + ti ´ i))/ td
ic =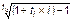
dc =

.

Таблица 6.5

i =
d =	(1 – 1/(1 + ti ´ i))/ td
ic =
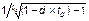
dc =

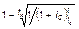
С использованием полученных данных из табл. 6.4, 6.5 теперь можно легко определять значения эквивалентных ставок для произвольных и различных по величине сроков t, на которых действуют рассматриваемые ставки.

Рассмотрим пример: пусть свободные денежные средства, могут быть размещены на срок 3,5 года под простую ставку i = 12%. Требуется определить значение сложной ставки i_c, которая за 2 года даст ту же наращенную сумму.

Для решения этой задачи достаточно воспользоваться выражением (6.5) из которого, после подстановки данных и вычислений получим i_c = 16,61%.

Следует отметить, что в задачах о нахождении эквивалентных значений ставок с одинаковыми временными сроками операций наращения или дисконтирования можно говорить о том, что эквивалентные ставки приводят к одинаковым финансовым результатам. В то время как в задачах о нахождении эквивалентных значения ставок при различных временных периодах использовать термин «одинаковый финансовый результат» некорректно.

Так в рассмотренном выше примере тот же объем финансовых средств был получен раньше на полтора года при смене условий размещения исходных средств с простой ставки наращения на эквивалентную сложную ставку. Получаемый один и тот же объем денежных средств это совсем не один и тот же финансовый результат, поскольку равные по величине суммы средств были получены в разное время. Это только арифметически (бухгалтерски) одинаковый результат. В рассмотренном примере по условиям задачи он достигнут с разницей в полтора года и с точки зрения финансовой логики это более «ценный» результат, поскольку он получен раньше. Действительно, средства, полученные раньше на полтора года можно использовать снова и за полтора оставшихся года их можно приумножить.

ПРИМЕР 1. Найти значение ставки простого дисконтирования эквивалентное ставке простых процентов i = 15% за 4,5 года.

Решение: Коэффициент наращения по ставке наращения простых процентов i = 0,15 за 4,5 года равен (1 + 0,15 ´ 4,5) = 1,675. Коэффициент наращения за 4,5 года по простой ставке дисконтирования d определяется выражением 1/(1 – d ´ 4,5). Из условия эквивалентности они должны быть равны, следовательно, из соотношения 1/(1 – d ´ 4,5) = 1,675 найдем искомое значение ставки дисконтирования d = (1 – 1/1,675)/4,5 = 0,089. То есть значение эквивалентной ставки дисконтирования равно d = 8,9%.

ПРИМЕР 2. Для сложной ставки дисконтирования d_c = 2% действующей на периоде времени 2 года найти эквивалентную ставку простых процентов i.

Решение: Коэффициент дисконтирования за два года при сложной ставке дисконтирования d_c = 0,02 равен (1 – 0,02)2 = 0,9604. Коэффициент дисконтирования по простой ставке i за два года определяется соотношением 1/(1 – 2 ´ i). Приравнивая их друг другу получаем выражение 1/(1 – 2 ´ i) = 0,9604 из которого определяется значение искомой ставки i = 1 – 1/0,9604 = 0,0412 или i = 4,12%.

ПРИМЕР 3. Сколько времени потребуется для достижения результата наращения 2,5 летнего депозита со сложной ставкой i_c = 6% при использовании эквивалентной ставки дисконтирования величиной d_c = 0,5%.

Решение: Приравняем коэффициенты наращения или после подстановки значений (1 + 0,06)^2,5 = 1/ откуда выразим = 1/(1 + 0,06)^2,5 или 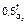= 0,8444 откуда t_dc = ℓog0,8444/ℓog0,5 = 0,236 лет. То есть примерно 86 дней.

Упражнения

1. Какая ставка наращения сложных процентов эквивалентна за четыре года ставке, дающей за это же срок коэффициент наращения равный 2,75.Ответ: 28,77%

2. Найти значение простой учетной ставки, эквивалентной сложной ставке наращения для трехлетней операции дисконтирования с коэффициентом дисконтирования 0,87. Ответ: 4,98%

3. Какой коэффициент дисконтирования даст простая ставка наращения эквивалентная сложной ставке дисконтирования в размере 2,55% на временном периоде в семь лет. Ответ: 0,83

4. Для сложной ставке наращения в 5%, действующей в течение 4 лет найти значение эквивалентное значение сложной учетной ставки для отрезке времени 3,5 года. Ответ: 5,4%

5. Каково значение простой ставки наращения эквивалентное сложной ставки дисконтирования 3% за семь лет. Ответ: 3,39%

6. За какой срок будет достигнут результат 4 летнего депозита со сложной ставкой 4%, если использовать сложную учетную ставку в вдвое меньше. Ответ: 0,72 года.

7. Определить величину простой учетной ставки с января 2003 г. по февраль 2005 г., которая эквивалентна сложной учетной ставке в 4,5% за семь с половиной месяцев. Ответ: 3,26%

8. Сколько полных лет потребуется, если использовать простую ставку наращения в 7%, что бы достичь результатов наращения по сложной учетной ставке в 11% за два года. Ответ: 3 года

ВОПРОСЫ

1. Эквивалентность ставок. Случай равенства временных периодов при определении значений эквивалентных ставок.

2. Эквивалентность ставок. Случай различных временных периодов при нахождении значений эквивалентных ставок.

3. Уравнения для определения эквивалентных значений простых и сложных ставок.

4. Уравнения эквивалентности ставок для процессов наращения и дисконтирования.

5. Условие получения уравнений для нахождения эквивалентных значений ставок при наращении.

6. Условие получения уравнений для нахождения эквивалентных значений ставок при дисконтировании.

 

Лекция 7