Цели урока: 1) повторить алгоритм вычитания трехзначных чисел без перехода через разряд;
2) перенести алгоритм вычитания трехзначных чисел с переходом через разряд на многозначные числа.
3) развивать навык устных и письменных вычислений;
4) снижать уровень тревожности на уроке;
5)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
4. Работа по учебнику
 (У) Задания 8, 7, 5*.
(У) Задания 8, 7, 5*.
Задание 5*.
1) 20: 5 = 4 (ябл.)
2) 4 • 2 = 8 (ябл.)
Ответ: в одном пакете 4 яблока, а в двух других по 8 яблок.
Задание 7. Числа, при которых неравенства будут верными, дети находят перебором. Например, в задании а):
60: 1 > 4 (да) 60: 20 > 4 (нет)
60: 5 > 4 (да) 60: 30 > 4 (нет)
Задание 8. а) 18 прямоугольников, из них 8 квадратов; 10 прямоугольников не являются квадратами. Прямоугольников (не квадратов) на 2 больше, чем
квадратов (10 - 8 = 2).
б) Прямоугольников — 11, квадратов — 6, не квадратов — 5; 6 - 5 = 1.
5. Работа в тетрадях
(П) Задания 4, 3, 6, 1, 2, 9.
Задание 1. Сначала ученики внимательно рассматривают образец приведенного в таблице примера вычитания, обращают внимание на то, как напечатаны числа в таблице, как подписаны друг под другом, объясняют значение нуля в записи числа 2043. После этого подробно рассматривается процесс «дробления» и замены 1 единицы высшего разряда 10 единицами низшего соседнего разряда: «Из трех единиц нельзя вычесть 8 единиц. Возьмем один десяток и за  меним его 10 единицами. Из нуля сотен также нельзя вычесть 5 сотен. Возьмем одну тысячу и заменим ее 10 сотнями. В таблице видно, что единиц после дробления стало 13, десятков — 3 (на один меньше), сотен — 10, тысяч — 1 (на одну меньше).
меним его 10 единицами. Из нуля сотен также нельзя вычесть 5 сотен. Возьмем одну тысячу и заменим ее 10 сотнями. В таблице видно, что единиц после дробления стало 13, десятков — 3 (на один меньше), сотен — 10, тысяч — 1 (на одну меньше).
Сейчас можно выполнять вычитание чисел поразрядно: из единиц — единицы, из десятков — десятки, из сотен — сотни, из тысяч — тысячи. При записи вычитания в столбик ученики ставят для памяти точки над теми разрядами, которые подвергались дроблению.
Аналогично объясняется вычитание чисел 5028 и 1654.
1. Вычитаю единицы: 8 ед. - 4 ед. = 4 ед. Пишу под единицами.
2. Вычитаю десятки: 2 дес. - 5 дес. — нельзя вычесть. Нужно взять одну единицу следующего разряда — сотню. Однако в разряде сотен нет единиц.
Возьмем одну единицу в разряде тысяч — это 10 сотен. Одну из этих сотен переносим в разряд десятков — это 10 десятков: 10 дес. + 2 дес. = 12 дес.
Выполняю вычитание: 12 дес. - 5 дес. = 7 дес. Пишу под десятками.
3. Вычитаю сотни. В разряде сотен — 9 единиц: 9 с.- 6 с. = 3 с. Пишу под сотнями.
4. Вычитаю тысячи. В разряде тысяч — 4 единицы: 4 тыс. - 1 тыс. = 3 тыс. Пишу под тысячами.
5. Читаю ответ: 3374.
Задание 2. Примеры решаются на доске и в тетрадях с подробным комментированием. 
 Задание 3.
Задание 3.
2000 + 24 500 + 2300 + 1700 = 30 500 (м2) = 3 га 500 м2
Физкультминутка
Задание 4. Сложение выполняется в столбик.
27 т 495 кг+ 9 т 780 кг = 27 495 кг+ 9780 кг = 37 275 кг = 37 т 275 кг
19 кг 450 г + 7 кг 080 г = 26 кг 530 г
28 м 75 см + 143 м 87 см = 2875 см + 14 387 см = 17 262 см = 172 м 62 см
5 ц 25 кг + 9 ц 87 кг = 525 кг + 987 кг = 1512 кг = 15 ц 12 кг = 1 т 512 кг
Задание 6. Получатся такие примеры:
3789 5723 4468
+ 2857+6282+3751
6646 12005 8219
Задание 9. Действия сложения и вычитания для нахождения неизвестных компонентов выполняются в столбик.
х + 23 856 = 497 943
х = 497 943 - 23 856
х = 474 087
474 087 + 23 856 = 497 943
497 943 = 497 943 -
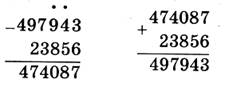 |
135 487 + а = 567834; а = 432 347.
Д) Задания 10, 11.
Задание 10.
 |


 Способ I. 84: 12 =7 (т); 7 ∙ 9 = 63 (т);
Способ I. 84: 12 =7 (т); 7 ∙ 9 = 63 (т);
84 + 63 = 147 (т).
Способ II. 84: 12 = 7 (т); 12 + 9 = 21 (рейс);
7 • 21 = 147 (т).
Задание 11.
4812; 6735; 6175; 75 179.
7. Подведение итогов урока 8.рефлексия
Урок 56






