Абсолютні статистичні величини пов'язані з фізичною і соціально-економічною суттю явищ, які вивчаються. Вони визначають їх розміри іменованими числами (наприклад, видобуток вугілля вимірюється тонами, газу - м3, тканини - м2). У більшості абсолютні величини як узагальнюючі показники - сумарні. В їх складі виділяють показники чисельності сукупності (наприклад, чисельність підприємств, сімей) і обсягу ознак (наприклад, продукція, прибуток). Розрізняють три групи вимірників:
- натуральні - відображають притаманні фізичні властивості (наприклад, міри ваги, довжини, часу). В певних випадках характеристика певних суспільних явищ вимагає одночасного використання двох і більше показників (наприклад, випуск електродвигунів характеризується їхньою кількістю - шт. і сумарною потужністю - кВт). Іноді використовуються комбіновані показники (наприклад, для електроенергії - кВт./год., вантажообороту - т/км). У разі потреби зводять воєдино кілька показників і отримують умовно-натуральні вимірники (наприклад, у сільському господарстві різні види великої рогатої худоби обчислюють умовними головами);
- трудові - використовують для вимірювання витрат праці на виробництво продукції чи виконання окремих робіт, для визначення продуктивності праці з метою раціонального використання трудових ресурсів (наприклад, люд./год., люд./день).;
- вартісні - дають змогу узагальнити і зіставити різноманітні явища (наприклад, вимірювання товарообороту, прибутку, капіталовкладень).
Багато абсолютних величин представляються у формі балансу, який передбачає розрахунок показника за такими двома розділами:
1) за джерелами формування;
2) за напрямами використання.
Відносні величини
Відносні величини відображають кількісні співвідношення соціально-економічних явищ, мають алгебраїчну форму представлення у вигляді частки від ділення двох одно- чи різнойменних величин. Знаменник - база порівняння або основа від величини. Наприклад, чисельність населення України у 1989 році становила 51,4 млн. чол., у 1959 - 41,9 млн. чол. Зіставлення цих величин говорить, що за 30 років кількість населення зросла в 1,226 рази або становила 122,6% від 1959 року, або збільшилась на 22,6%.
Співвідношення різнойменних абсолютних величин утворює відносну величину інтенсивності (Наприклад, густина населення, рівень економічного розвитку регіону, виробництво продукції на душу населення). Від величини інтенсивності характеризують ступінь поширення чи розвитку явища в певному середовищі (наприклад, показник народжуваності, інтенсивності міграційних потоків тощо).
Порівняння однойменних статистичних величин використовують для вирішення таких аналітичних задач:
- характеристика структури сукупності;
- оцінка інтенсивності розвитку явищ;
- оцінка виконання плану та дотримання норм чи стандартів.
Відповідно до цих задач виділяють такі види відносних величин:
- показники структури;
- показники координації;
- показники динаміки;
- показники виконання планового завдання;
- показники дотримання норм і стандартів.
Статистичний аналіз на основі показників розкриває зміст і значення показника, поглиблює уяву про предмет дослідження (його закономірності) здійснюється за двома напрямами:
1. розглядає зв'язки і відношення, виявляє фактори впливу на рівень і варіацію показників, оцінює ефект їх впливу;
2. вивчає динаміку показників, напрям і швидкість змін, оцінює ефект їх впливу.
Тема 5. СЕРЕДНІ ВЕЛИЧИНИ ТА ЇХ ВИДИ
Аналіз варіаційного ряду розподілу полягає у виявленні закономірностей зміни частот залежно від зміни кількісної ознаки, яка покладена в основу групування.
При аналізі варіаційних рядів найчастіше використовуються такі групи показників:
1) характеристики центру розподілу;
2) характеристики розміру варіації;
3) характеристики форми розподілу.
Центр розподілу - це значення змінної ознаки, навколо якого групуються інші варіанти. Характеристиками центру розподілу є:
- середня;
- мода;
- медіана;
- кадриль або чверть;
- десята частина.
Середня величина - це узагальнюючий показник, який характеризує сукупність однотипових явищ (процесів) за змінною кількісною ознакою. Вона показує типове характерне значення ознаки, віднесене до одиниці статистичної сукупності.
В середній величині нівелюються індивідуальні відмінності одиниць сукупності, які зумовлені дією випадкових факторів, і виділяється загальне.
Основними умовами використання середніх величин є:
1) однорідність статистичної сукупності;
2) обґрунтований вибір форми середньої величини.
Вибір форми розрахунку середніх залежить від виду ряду статистичних даних, змісту ознаки, мети використання.
Таблиця 5.1
Види середніх
| Вид середньої | Проста | Зважена | |
| арифметична | 
| 
| (5.1)-(5.2) |
| гармонійна | 
| 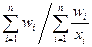
| (5.3)-(5.4) |
| геометрична | 
| 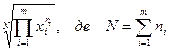
| (5.5)-(5.6) |
| квадратична | 
| 
| (5.7)-(5.8) |
| хронологічна | 
| 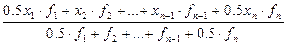
| (5.9)-(5.10) |
де xi - значення ознаки; wi - вага ознаки ( ); n - обсяг сукупності.
); n - обсяг сукупності.
Обчислення середньої арифметичної для дискретного варіаційного ряду може виконатись за формулами простої чи зваженої середньої. В інтервальному ряді попередньо визначають центральні значення відповідних інтервалів і, таким чином, переходять до дискретного ряду. Зауваження: якщо початковий чи кінцевий інтервал в ряді є відкритими, то його довжину слід брати рівною довжині ближчого інтервалу.
Середня арифметична проста - найбільш поширена форма розрахунку (наприклад, середня температура за тиждень). Наприклад. Було зроблено замовлення на 3, 4, 5, 8 грн. Середня вартість замовлення: знаходимо як (3+4+5+8)/4=5.
Середня арифметична зважена теж часто застосовується. Наприклад, в магазині було зроблено 4 замовлень по 3 грн.; 10 замовлень по 10 грн. та 6 замовлень по 20 грн. Середня вартість замовлення складає (3×4+10×10+20×6)/(4+10+6)=12,1 грн.
Якщо сукупність складається з К груп, значення середньої арифметичної розраховують за формулою:

| (5.11) |
Наприклад, знайти середнє значення успішності потоку, коли відомо середню успішність по групах та число студентів у кожній групі.
Під час розрахунку середньої арифметичної зваженої можна використати відносні частоти.

| (5.12) |
Середня гармонійна вживається тоді, коли не задана чисельність сукупності, а ваги wi визначаються як добутки значень варіанти ознаки на її чисельність.
Наприклад, розрахувати середню врожайність двох полів. Врожайність першого поля 20ц/га, а зібрали 400ц. Врожайність другого поля 25ц/га, а зібрали 1000ц.

Середня геометрична вживається при аналізі рядів динаміки для розрахунку середніх коефіцієнтів темпів зміни.
Наприклад, у 2001 році підприємство наростило випуск продукції на 21%, а у 2002 - на 44%. Знайти середній темп зростання за три роки.

Для аналізу часових рядів часто використовують середню хронологічну. Вона дуже часто вживається, коли відомості даються на певний зріз часу.
Наприклад, чисельність потоку студентів спеціальності ЕК становив на 1.09.2001р. - 160 чол., 1.09.2004р. – 200чол., 1.09.2005р. - 140 чол.

Середня квадратична належить до класу степеневих середніх. Як правило, застосовується для вимірювання варіації.
Крім середніх величин важливу роль відіграють мода і медіана.
Мода - це найбільш поширене значення ознаки. Мод може кілька для одного ряду. У інтервальному ряді після визначення модального інтервалу можна точно визначити значення моди за формулою

| (5.13) |
XМо - ліва границя модального інтервалу;
hМо - ширина модального інтервалу;
fМо - частота модального інтервалу;
fmo-1 - частота інтервалу, який передує модальному;
fmo+1 - частота інтервалу, який слідує за модальним.
Наприклад, задано такий розподіл заробітної плати
Таблиця 5.2
Розподіл заробітної плати серед працівниками підприємства
| Заробітна плата, грн.. | менше 300 | 300-400 | 400-500 | 500-600 | 600-700 | 700-900 | більше 900 |
| Кількість працівників, чол.. | 10 | 25 | 48 | 32 | 28 | 22 | 8 |
Модальний інтервал – 400-500 грн., а мода знаходиться так

Цю ж величину можна знайти методом геометричної перебудови.
Медіана - це варіанта, яка розміщена посередині впорядкованого варіаційного ряду. Медіана ділить весь ряд на дві однакові частини за чисельністю одиниць сукупності.
 , ,
| (5.14) |
де SMe - сума нагромаджених частот перед медіанним інтервалом.
Наприклад, в рамках попередньої задачі медіанний інтервал – 500-600 грн., а мода знаходиться так:
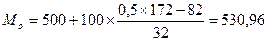
Тема 6. ПОКАЗНИКИ ВАРІАЦІЇ
Середні величини дають загальну характеристику сукупності. Типовість і надійність середньої характеристики залежить від розміру і розподілу відхилень значення ознаки від середньої.
Таблиця 6.1
Показники, за допомогою яких вимірюють відхилення від середньої
| Види відхилення | просте | зважене | |
| Середнє арифметичне лінійне відхилення | 
| 
| (6.1)-(6.2) |
| Середнє квадратичне арифметичне відхилення | 
| 
| (6.3)-(6.4) |
| Центральний момент k-ого порядку | 
| 
| (6.5)-(6.6) |
До характеристик виду розподілів також відносять
Таблиця 6.2
Характеристики форми розподілу
| Розмах варіації | різниця між найбільшим і найменшим значенням | 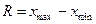
| (6.7) |
| Коефіцієнт асиметрії | характеризує несиметричність розподілу | 
| (6.8) |
| Коефіцієнт ексцесу | характеризує ширину рознесення даних у ряді розподілу | 
| (6.9) |
Крім даних величин широко застосовують такі відносні показники варіації:
Таблиця 6.3
Коефіцієнти варіації
| коефіцієнт варіації лінійний | 
| (6.10) |
| коефіцієнт варіації квадратичний | 
| (6.11) |
| коефіцієнт осциляції | 
| (6.12) |
Якщо сукупність розподілити на кілька груп за певними ознаками, то для характеристики впливу групувальних ознак на загальну варіацію ознаки використовують такі величини: 1) загальна дисперсія; 2) внутрішньогрупова дисперсія або середня з групових дисперсій; 3) міжгрупова дисперсія.
Для них задовольняється правило сумування дисперсій
 , ,
| (6.13) |
де
 , ,
| (6.14) |
 , ,
| (6.15) |
m – кількість груп; j – порядковий номер груп.
Наприклад, перевіримо правило сумування дисперсій на базі зібраних по групах 01, 02, 03 даних про кількість отриманих оцінок. В таблиці наведені первинні дані звичайним та розраховані результати нахиленим шрифтом
Таблиця 6.4
Перевірка правила сумування дисперсій
| Групи | Оцінка | Всього, студ. | Всього, бал | Середня оцінка, бал | Дисперсія, бал | ||||
| „3”, студ. | „4”, студ. | „5”, студ. | |||||||
| 4,307692 | ((3-4,043478)204+(4-4,043478)2·10+(5-4,043478)2·12)/26= | 0,520710 | |||||||
| 3,666667 | ((3-4,043478)2015+(4-4,043478)2·10+(5-4,043478)2·5)/30= | 0,555556 | |||||||
| 4,166667 | ((3-4,043478)2010+(4-4,043478)2·10+(5-4,043478)2·16)/36= | 0,694444 | |||||||
| Всього, студ. | |||||||||
| Всього, бал | 4,043478 | ||||||||
| Загальна | ((3-4,043478)2·26+(4-4,043478)2·30+(5-4,043478)2·36)/92= | 0,672023 | |||||||
| Внутрішньо групова | (0,520710·26+0,555556·30+0,694444·36)/92= | 0,600056 | |||||||
| Між групова | ((4,307692-4,043478)2·87+(3,666667-4,043478)2·87+(4,166667-4,043478)2·87)/92= | 0,071967 | |||||||
Тема 7. ВИБІРКОВЕ СПОСТЕРЕЖЕННЯ
Вибіркове спостереження – найбільш поширений вид несуцільного спостереження. Загальна сукупність однорідних об'єктів у статистиці називається генеральною сукупністю. Відібрана для дослідження частина генеральної сукупності називається вибірковою сукупністю. Наприклад, використовується для спостереження за обладнанням на промислових підприємствах, втрат при збиранні врожаю, попиту населення на певні види товарів, для обстеження сімейних бюджетів населення, вивчення громадської думки. При вибірковому спостереженні обстеженню підлягають не всі елементи сукупності, що вивчаються, а лише відібрана її частина. Порівняно з суцільним спостереженням, вибіркове має превагу, оскільки потребує менше коштів і часу, крім того дешевше обходиться статистична обробка інформації. Ці переваги мають місце лише при дотриманні наукових принципів його проведення, що дає можливість отримати репрезентативну вибірку для відображення характеристик генеральної сукупності. Вибірка називається репрезентативною, якщо кожний елемент генеральної сукупності має однакову ймовірність потрапляння у вибірку і відбір здійснюється випадковим чином. З поняттям репрезентативності тісно пов'язане поняття похибки вибірки – розбіжності між показниками генеральної і вибіркової сукупностей.
Розрізняють похибки вибірки:
1) систематичну – виникає через порушення правил випадкового вибору;
2) випадкову – виникає через недостатньо рівномірне представлення у вибірковій сукупності різних категорій генеральної сукупності.
У процесі вибіркового дослідження розрізняють два види вибіркових оцінок:
1) точкова оцінка – це значення параметра, обчисленого на основі даних вибірки (вибіркова середня);
2) інтервальна оцінка – довірчі інтервали (інтервал значення параметра з даною ймовірністю).
Найчастіше використовують такі способи відбору:
1) Простий випадковий – здійснюється за допомогою жереба або таблиць випадкових чисел. Цей спосіб дає кращі результати, якщо між елементами генеральної сукупності немає різних відмінностей.
2) Систематизований – передбачає, що основою вибірки є впорядкована чисельність елементів сукупності. Вибір елементів здійснюється через рівні інтервали. Крок інтервалу обчислюють через ділення сукупності на передбачений обсяг вибірки. Початковий елемент відбору визначають як випадкове число всередині 1-го інтервалу, другий та решта елементів залежать від початкового числа і кроку інтервалу.
3) Розшарований (районований) – спосіб формування вибірки з врахуванням структури генеральної сукупності. На відміну від попередніх відборів, цей передбачає попередню структуризацію генеральної сукупності і незалежний відбір елементів у кожній складовій частині.
4) Серійний проводиться таким чином, що обстеженню підлягають повні серії. Серія – це така сукупність елементів у генеральній вибірці, яка поєднана організаційними або територіальними зв'язками. Наприклад, перевірка успішності на потоці може проводитись шляхом обстеження лише однієї групи.
Розрізняють два види випадкового відбору:
1) повторна вибірка;
2) безповторна вибірка.
Середня стандартна похибка вибіркової середньої для безповторної вибірки:
 , ,
| (7.1) |
де N – чисельність (обсяг) генеральної сукупності; n – обсяг вибіркової сукупності.
Середня стандартна похибка вибіркової середньої для повторної вибірки:
 . .
| (7.2) |
Для невеликих за розміром вибірок відповідно використовують такі формули:
 , ,
| (7.3) |
Необхідний обсяг вибірки при дослідженні із заданою точністю встановлюють за формулою:
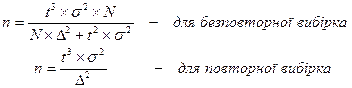 , ,
| (7.4) |
де t – коефіцієнт довіри, визначається з таблиць Стьюдента залежно від Р; D - похибка. Гранична похибка D - це максимально можлива похибка для взятої ймовірності F(t).
 . .
| (7.5) |
Взаємозв’язок між m та F(t) легко простежити на рис. 4, де величина mt задає межі охоплення функції щільності розподілу імовірнісного розподілу, а F(t) - характеризує величину площі охопленої цими межами.
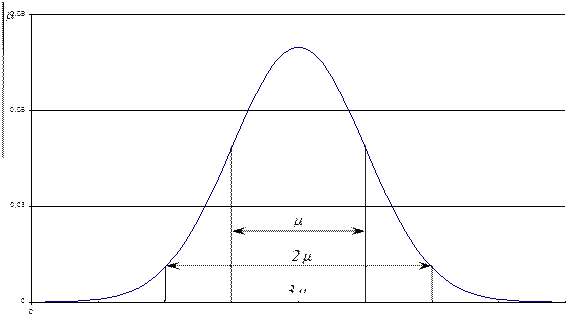
Рис. 2. Співвідношення ймовірності та величин відхилення.
Довірче число t показує, як співвідносяться гранична і стандартна похибки.
 . .
| (7.6) |
З рисунка 2 видно, що
Ø з ймовірністю 0,68 гранична похибка D не вийде за межі D = ±1m;
Ø з ймовірністю 0,95 гранична похибка D не вийде за межі D = ±2m;
Ø з ймовірністю 0,98 гранична похибка D не вийде за межі D = ±3m.
На практиці найчастіше застосовують ймовірність 0,95.
З попереднього матеріалу видно, що розмір граничної похибки залежить від величини варіації ознаки і від обсягу вибірки (m). Наприклад, проводиться вибіркове оцінювання середньої на прикладі обстеження 225 домогосподарств регіону. За результатами 1% вибірки 70% грошового доходу домогосподарств іде на харчування і середньодушові витрати на місяць становлять 82 грн. при дисперсії s2 = 8510.
Визначимо межі середньодушових витрат на харчування з ймовірністю 0,95.
 . .
| (7.7) |







