Статистична гіпотеза – це певне припущення щодо властивостей генеральної сукупності, яке можна перевірити опираючись на результати вибіркового спостереження. Суть перевірки гіпотез полягає в тому, щоб визначити, узгоджуються чи ні результати вибірки з гіпотезою, випадковими чи не випадковими є розбіжності між гіпотезою і даними вибірки. Найчастіше гіпотеза, яку треба перевірити, формулюється як відсутність розбіжності (нульова розбіжність) між невідомим параметром генеральної сукупності G і заданою величиною А, а тому її позначають
| H0:G=A. | (7.16) |
Кожній новій гіпотезі протиставляють альтернативну. При її формулюванні враховується знак відхилення. Для додатних це буде H0:G>A, а для від'ємних H0:G<A. Якщо випадкові дані суперечать гіпотезі Но, то вона відхиляється.
Спираючись на результати вибірки статистична перевірка гіпотези неминуче пов'язана з ризиками прийняття помилкового рішення:
o ризик 1 – відхилення правильної нульової гіпотези;
o ризик 2 – невідхилення нульової гіпотези, коли правильною є альтернативна.
Ці ризики є конкуруючими: зменшення одного приводить до збільшення іншого. Оскільки уникнути ризиків неможливо, а їх наслідки, як правило, різновагомі, то в кожному конкретному випадку прагнуть мінімізувати ризик понести найбільші втрати.
Таблиця 7
Гіпотези та ймовірність їх прояви
| Правильна гіпотеза | Прийнята гіпотеза | |
| a | 1-a | |
| Ho | a | 1-a |
| Ha | 1-b | b |
Правило, за яким гіпотеза Но відхиляється (приймається), називається статистичним критерієм. Матеріальною основою будь-якого критерію є статистична характеристика Z, значення якої визначається за даними вибірки, а закон розподілу відомий.
Кожне значення характеристики Z має певну ймовірність F(Z). Якщо вибіркове значення Z малоймовірне – гіпотеза Hz відхиляється. Межі мало ймовірності називають рівнем істотності. За змістом – це ймовірність ризику (a). Тому залежно від змісту гіпотези Но і наслідків відхилення рівень істотності задається у кожному конкретному дослідженні. Як правило, це 0,1; 0,05; 0,025; 0,01. Значення статистичної характеристики критерії Z (Z1-a) поділяє множину вибіркових значень Z на дві частини: 1) область допустимих значень; 2) критичну область. Залежно від того, як сформульована альтернативна гіпотеза, критична область може бути односторонньою та двосторонньою.
Якщо вибіркові значення Z потрапляють в критичну область, то гіпотеза Но відхиляється, і приймається якщо Z попадає в область допустимих значень.
Статистична гіпотеза перевіряється так: 1) формулюється Но і На; 2) вибирається статистична характеристика Z за значеннями якої перевіряють правильність гіпотези Но; 3) визначають рівень істотності і відповідно критичне йому значення (залежно від формування гіпотези це може бути одностороння чи двостороння область); 4) за результатами розраховують фактичне (вибіркове) значення статистичної характеристики Z(1-a); я кщо Z> Z1-a - гіпотеза Но відхиляється, в іншому випадку для Z< Z1-a - гіпотеза Но приймається.
Тема 8. СТАТИСТИЧНІ МЕТОДИ АНАЛІЗУ ВЗАЄМОЗВ'ЯЗКІВ
Усі явища навколишнього світу, особливо соціально-економічні, взаємопов'язані і взаємообумовлені. Кожне явище є наслідком дії певної множини причин і водночас є причиною для інших явищ. Причини і явища можуть бути пов'язані прямо або опосередковано.
Головна мета вимірювання взаємозв'язків – дати кількісну характеристику причинних зв'язків. Вивчаючи закономірності зв'язку причини та наслідки об'єднують в одне поняття – фактор. Відповідно ознаки, які характеризують фактори, називають факторними. Часто, ті ознаки, які характеризують причини називають незалежними, а ті, що характеризують наслідки, називають результативними.
Розрізняють два типи зв'язків: функціональні та стохастичні.
У разі функціонального зв'язку кожному значенню фактора х відповідає чітко визначене значення (множина значень) y. Наприклад, залежність довжини ртутного стовпчика від температури навколишнього середовища. Знаючи х в кожному випадку точно визначається результат y. На відміну від функціональних стохастичні зв'язки неоднозначні. Наприклад, залежність захворюваності населення від екологічного стану довкілля. На забруднених радіонуклідами територіях, як і на інших стан здоров'я мешканців коливається від тяжко хворого до практично здорового. Хоча в середньому там захворюваність значно вища.
Стохастичні зв'язки виявляються як узгодженість варіації двох чи більше ознак. У зв'язку y=f(x), кожному значенню х відповідає множина значень y, яка утворює так званий умовний розподіл. Якщо умовні розподіли замінюються одним параметром -  , то такий зв'язок називається кореляційним. Наприклад, при проведенні валютних операцій, протягом дня, для переведення суми в національній валюті в еквівалентну їй суму в іноземній валюті, використовують валютний курс.
, то такий зв'язок називається кореляційним. Наприклад, при проведенні валютних операцій, протягом дня, для переведення суми в національній валюті в еквівалентну їй суму в іноземній валюті, використовують валютний курс.
Можна говорити, що аналіз взаємозв'язків полягає не лише у підтвердженні (відхиленні) тверджень про наявність кореляційного зв'язку між факторною ознакою " х " і результативною "y", а й визначенні, як у середньому змінюється " y " в залежності від " х ". Ефекти впливу на " y " визначаються відношенням приростів середніх групових цих величин.
Розрізняють такі види зв'язків:
1) адаптивні (наприклад, а + b + c);
2) мультиплікативні (наприклад, a ´ b ´ c);
3) залежності середніх величин від структури сукупності.
Регресійний аналіз.
Важливою характеристикою кореляційного зв'язку є лінія регресії. Наприклад, залежність врожайності від кількості опадів описується параболічною функцією. Емпірична при використанні аналітичного групування і теоретична в моделі регресійного аналізу. Емпірична будується з використанням групових середніх резервної ознаки " y ", кожна з яких належить до відповідного інтервалу х. Теоретична лінія регресії описується функцією y = f (x). Наприклад, залежність маси чоловіка до 30 років від росту описується формулою y=x–100.
Різні явища по-різному реагують на зміну факторів. У регресійному аналізі крім звичайного, лінійного зв'язку y = a + bx використовують такі функції:
1) степеневу y = a ´ b
2) гіперболічну y = a + b/x
3) параболічну y = a + b x + с x2
Звичайно є ще й інші форми представлення. При визначенні зв'язку між собівартістю та обігом продукції використовується рівняння регресії.
Метод найменших квадратів
Нехай задано деякий набір спостережень, які складаються із впорядкованих пар 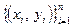 . Ця множина часто представляється у вигляді таблиці. Ці дані називатимемо фактичними значеннями. Задача полягає у побудові кореляційної залежності між цими величинами x, y.
. Ця множина часто представляється у вигляді таблиці. Ці дані називатимемо фактичними значеннями. Задача полягає у побудові кореляційної залежності між цими величинами x, y.
Щоб дослідити взаємозв'язок між факторами нанесемо точки на площину x0y. В результаті отримаємо так звану "хмарку", яка містить точки (xi, yi). В залежності від поведінки цієї "хмарки" можна визначити той чи інший вид лінії регресії (параболічний, лінійний, степеневий). Припустимо, що взаємозв'язок лінійний: y = a +bx.
Рівняння регресії шукаємо у вигляді
 . .
| (8.1) |
Лінія регресії будується таким чином, щоб відхилення  для будь-якого хі де
для будь-якого хі де  розраховується через підстановку хі в рівняння регресії
розраховується через підстановку хі в рівняння регресії  , а
, а  - фактичне значення з таблиці. Вимогу, яка визначає коректність побудови рівняння регресії описується функціоналом:
- фактичне значення з таблиці. Вимогу, яка визначає коректність побудови рівняння регресії описується функціоналом:
 . .
| (8.2) |
Підставимо залежність теоретичного значення у шукане рівняння регресії.
 . .
| (8.3) |
Для того, щоб отримати значення мінімуму функціоналу потрібно задовольнити умовам:
 . .
| (8.4) |
Підставивши (8.1) в (8.3) та виконавши перетворення, отримаємо:
 . .
| (8.5) |
Розкривши дужки, отримаємо:
 . .
| (8.6) |
Звідси можна вивести формули для знаходження a і b.
 , ,  . .
| (8.6) |






