Наличие внутреннего трения в газах обычно иллюстрируют на следующем примере. Рассмотри газ, находящийся между двумя параллельными пластинками АВ и CD. При движении пластинки CD появляется сила, действующая на пластинку АВ и направленная в сторону движения. Эта сила и есть сила внутреннего трения. Впрочем, о внутреннем трении можно говорить лишь тогда, когда расстояние между пластинками АВ и CD очень велико по сравнению со средней длиной свободного пробега молекулы газа:
h>>λ.
Тогда от наличия пластин можно отвлечься и говорить о силах, действующих внутри самого газа. Будем представлять себе газ неограниченным и движущимся стационарно плоско-параллельными слоями в горизонтальном направлении. Скорость этого макроскопического движения и меняется в направлении, перпендикулярном к слоям. Это направление мы примем за ось Y. Таким образом, мы предполагаем, что и = и(y). Рассечем мысленно газ на две половины плоскостью АВ, параллельной слоям. Допустим для определенности, что скорость и(y) возрастает с возрастанием y. Тогда верхняя половина газа будет действовать на нижнюю с силой, направленной вправо, а нижняя на верхнюю — с силой, направленной влево. Это и есть силы внутреннего трения. С молекулярной точки зрения происхождение сил внутреннего трения объясняется следующим образом. Если бы газ покоился, то все направления скоростей его молекул были бы равновероятны. Средняя скорость и среднее количество движения каждой молекулы были бы равны нулю. При наличии упорядоченного движения газа средняя скорость молекулы не нуль, а равна u = u (y). С этой скоростью связано количество движения g = т u, которым обладает рассматриваемая молекула. Такое количество движения условимся называть упорядоченным. Молекулы, лежащие над плоскостью АВ, обладают большим упорядоченным количеством движения, чем молекулы, расположенные под ней. Переходя из пространства над плоскостью АВ в пространство под ней, молекулы передают часть своего упорядоченного количества движения молекулам, с которыми они сталкиваются в пространстве ниже плоскости АВ. Это проявляется в том, что газ, расположенный ниже этой плоскости, подвергается действию силы, направленной в сторону скорости u. Аналогично, более медленные молекулы, попадая из «нижнего» пространства в «верхнее», при столкновениях отнимают часть упорядоченного количества движения умолекул, расположенных над плоскостью АВ. В результате газ в верхнем пространстве испытывает тормозящую силу, направленную против скорости u. Эти силы и являются силами внутреннего трения.
Исследуем теперь явление внутреннего трения количественно. Рассмотрим сначала предельно упрощенный расчет. Будем считать скорости теплового движения всех молекул одинаковыми и равными v.
Кроме того, при рассмотрении теплового движения будем рассуждать так. Если бы у нас не было направленного движения газа, то все направления при тепловом хаотическом движении были бы равноправны. Выделим мысленно какой-то объем газа. Чтобы понять, как молекулы выходят за пределы этого объема, можно ввести допущение, что молекулы движутся только параллельно координатным осям, а именно так, что 1/6 всех молекул движется в положительном направлении оси X, 1/6 – в отрицательном направлении и аналогично для двух оставшихся осей. Если мы рассмотрим на границе объема элементарную площадку dS, то с ней будут сталкиваться только движущиеся в одну сторону молекулы. Число таких молекул в единице объема составит
.
За время dt с площадкой dS столкнутся все молекулы рассматриваемой группы, которые лежат внутри цилиндра с основанием dS и высотой vdt. Число молекул в этом цилиндре, движущихся к стенке, равно
.
Соответственно, среднее число молекул, сталкивающихся в единицу времени с единичной площадкой, будет
.
В случае направленного движения газа мы также можем считать, что все молекулы разделены на шесть одинаковых потоков, параллельных координатным осям. Одна шестая всех молекул будет двигаться сверху вниз, одна шестая — снизу вверх. Только молекулы этих двух потоков и участвуют в передаче количества движения. Молекулы остальных четырех потоков движутся параллельно плоскости АВ. Они влияют на среднюю длину свободного пробега λ, но к передаче количества движения прямого отношения не имеют. На тепловое движение молекул сверху вниз и снизу вверх накладывается упорядоченное движение вправо, причем скорость этого движения u однозначно определяется положением молекулы, точнее, ее координатой y. Будем предполагать, что изменения упорядоченной скорости u на длине свободного пробега очень малы по сравнению с тепловой скоростью v. Тогда можно выбрать такую систему отсчета, в которой упорядоченная скорость u в интересующей нас части газа будет также очень мала по сравнению с тепловой скоростью v. В дальнейшем движение рассматривается именно в такой системе отсчета.
Возьмем на плоскости АВ единичную площадку S. Начало координат поместим в той же плоскости. Подсчитаем количество движения, ежесекундно переносимое молекулами газа через площадку S. Число молекул, пересекающих площадку S сверху вниз в единицу времени, определяется формулой
.
Пусть N из этих молекул прошли перед площадкой путь y без столкновений. Число N определяется формулой
.
Отсюда находим, что число молекул, претерпевших последнее столкновение в слое между y и y + dy, равно
.
При столкновении в этом слое молекула получает количество движения g(y) и, двигаясь далее без столкновений, переносит эту величину через площадку S. Количество движения, переносимое в единицу времени через площадку S всеми N 0 молекулами, определяется интегралом
.
Так как на длине свободного пробега скорость u меняется мало, то функцию g(y) можно разложить по степеням y, оборвав это разложение на линейном члене, т.е
.
В этом приближении
.
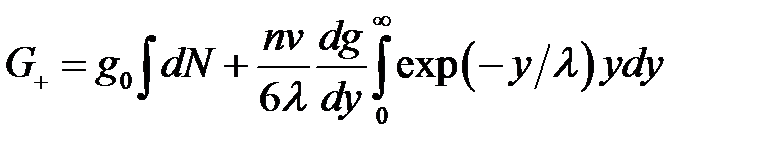Вычислив интегралы, найдем
.
Заметим, что это выражение можно записать в виде
.
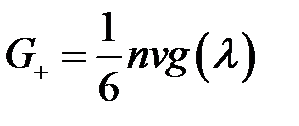Отсюда видно, что при вычислении G+ можно рассуждать так, как если бы все молекулы, летящие к площадке S, претерпевали последние столкновения на расстоянии λ от этой площадки и далее двигались к ней без столкновений.
Отметим, что концентрация п может меняться в пространстве. Однако это обстоятельство никак не отразится на справедливости полученной формулы. Действительно, из вывода ясно, что под п следует понимать значение концентрации на самой площадке S, независимо от того, рассматривается ли верхний или нижний пучки молекул, участвующих в переносе величины g. Было бы грубой ошибкой считать, что концентрацию п надо брать на расстоянии ±λ от площадки S, где молекулы претерпели «последние столкновения». Такой способ расчета должен применяться только к переносимой величине g, но не к концентрации п.
По аналогии с можно утверждать, что молекулы, летящие снизу вверх, переносят в том же направлении количество движения
.
Полное количество движения, ежесекундно переносимое через площадку S в положительном направлении оси Y (снизу вверх), найдется вычитанием из последней формулы предыдущего результат. Оно равно
.
Этот перенос проявляется в том, что вдоль плоскости АВ действует вязкое касательное напряжение
,
где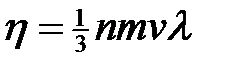 
.
Мы получили не только ньютоновский закон внутреннего трения, но и нашли выражение для коэффициента внутреннего трения η.
Но как мы видели при рассмотрении понятия вязкости, тензор напряжений должен быть симметричным. В противном случае нарушался бы закон сохранения момента количества движения. Поэтому вязкие напряжения должны действовать не только в плоскостях течения газа, но и в плоскостях, перпендикулярным к ним. Необходимо поэтому выяснить, как возникают эти напряжения, и убедиться, что они удовлетворяют условию симметрии
.
Для этого рассмотрим бесконечно малую площадку dS,перпендикулярную к направлению течения газа. Таким образом, по-прежнему, предполагается, что газ течет параллельно оси X и рассматриваются группы молекул, тепловые скорости которых параллельны оси Y. Из-за наличия молекулярного течения, молекулы имеют боковую составляющую скорости и(y). Благодаря этому в рассматриваемом случае и появляется поток молекул, пронизывающий площадку dS. Рассмотрим пучок молекул, приходящих сверху. На основании доказанного выше можно рассуждать так, как если бы все молекулы пучка совершили последние столкновения на расстоянии λ от площадки dS (измеренном вдоль оси Y). Количество таких молекул, пронизывающих площадку dS в единицу времени, равно
.
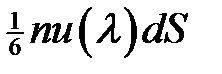Переносимое ими количество движения будет
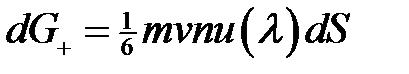
и направлено вниз. Поток молекул, приходящих снизу, будет меньше, а именно
,
Связанный с ними поток количества движения равен
и направлен вверх. Разность этих двух потоков
даст полный поток количества движения, переносимый через площадку dS вверх в единицу времени. Он проявляется в появлении касательного напряжения. Если у величины потока изменить знак, то мы получим интересующую нас силу
,
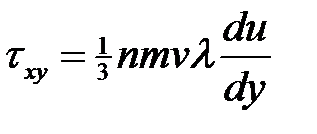которое действует в плоскостях, перпендикулярных к направлению течения газа. Таким образом, мы выяснили происхождение «поперечных» касательных напряжений и доказали, что .
Если мы учтем, что на самом деле молекулы распределены по скоростям и движутся не параллельно осям равными потоками, то можно показать, что в этом случае
.
Совершенно так же может быть рассмотрено явление теплопроводности. Здесь вместо переноса количества движения речь идет о переносе энергии. В классической теорииэнергия молекулы пропорциональна температуре и может быть представлена в виде
,
где cV — удельная теплоемкость газа при постоянном объеме (отношение количества теплоты, сообщённого газу, к изменению температуры δТ, которое при этом произошло). Пусть газ находится между двумя бесконечными проводящими плоскостями, перпендикулярными к оси Y, причем температуры их Т 1и Т 2 поддерживаются постоянными. Тогда будет происходить передача тепла совершенно так же, как в аналогичном случае происходит передача количества движения. Для вычисления потока тепла q можно воспользоваться формулой
,
заменив в ней импульс g на энергию . Тогда получится
.
или 
,
где ϰ =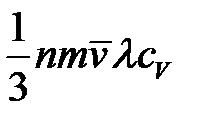 
– коэффициент теплопровоности газа.
Введя плотность газа ρ = nm, формулы для коэффициентов вязкости и теплопроводности можно переписать в виде
, 
.
Так как λ обратно пропорциональна ρ, то отсюда следует, что коэффициенты внутреннего трения и теплопроводности не зависят от плотности газа. К такому выводу впервые пришел Максвелл, и этот вывод показался ему парадоксальным. Однако опыты, поставленные самим Максвеллом и другими физиками, подтвердили указанный вывод. Независимость коэффициентов внутреннего трения и теплопроводности от плотности газа имеет простое объяснение. Если плотность газа велика, то в переносе импульса и энергии участвует много молекул. Однако передача импульса и энергии за время между двумя последовательными столкновениями производится малыми порциями и на малые расстояния. Если же плотность мала, то уменьшается и число молекул, участвующих в переносе. Но это уменьшение полностью компенсируется тем, что теперь молекулы переносят
импульс и энергию более крупными порциями и на большие расстояния.
Однако так будет происходить только до тех пор, пока плотность газа ρ не очень мала. Допустим, по-прежнему, что речь идет о передаче импульса или тепла от одной пластинки к другой, ей параллельной. Независимость коэффициентов η и ϰ от плотности ρ справедлива до тех пор, пока расстояние между пластинками d велико по сравнению с длиной свободного пробега λ. В противоположном случае, когда λ> > d, столкновения между молекулами самого газа в явлениях переноса перестают играть роль. Существенными становятся только столкновения молекул со стенками сосуда, в котором заключен газ. Молекула, столкнувшись с горячей стенкой, получает от нее кинетическую энергию и переносит ее к более холодной стенке, не испытывая промежуточных столкновений. То же можно сказать и о переносе импульса. Ясно, что в таком случае перенос тепла или импульса будет происходить тем медленнее, чем больше разрежен газ. Такой перенос формально может быть описан прежними формулами. Только теперь η и ϰ лишь условно можно назвать коэффициентами внутреннего трения и теплопроводности. Они зависят не только от свойств самого газа, но и от расстояния между пластинками. Их можно оценить прежними формулами, заменив величину λ на расстояние d между пластинками. Таким образом, независимость коэффициентов трения и теплопроводности от плотности газа имеет место лишь до тех пор, когда длина свободного пробега λ мала по сравнению с какими-то характерными размерами сосуда d (например, расстоянием между противоположными стенками, когда они параллельны). Когда λ и d становятся сравнимыми друг с другом, при уменьшении плотности коэффициенты η и ϰ начинают убывать. В дальнейшем это убывание идет по линейному закону: коэффициенты η и ϰ становятся пропорциональными плотности ρ. На этом основано устройство сосуда Дыоара. Пока расстояние d между двойными стенками сосуда Дьюара велико по сравнению с λ, откачка газа из пространства между этими стенками ничего не дает для теплоизоляции. Но она становится эффективной после перехода через промежуточную область, в которой λ ~ d.
11. Самодиффузия в газах.
Допустим, что закрытая горизонтальная трубка разделена на две части перегородкой. По одну сторону перегородки находится какой-то газ 1, а по другую — газ 2. Пусть давления и температуры обоих газов одинаковы. Если удалить перегородку, то газы начнут перемешиваться, причиной чему является хаотическое тепловое движение молекул. Спустя некоторое время концентрации компонентов смеси станут одинаковыми по обе стороны перегородки. Такое проникновение молекул одного газа в среду молекул другого газа называется взаимной или концентрационной диффузией газов. Для наблюдения диффузии трубку можно расположить и вертикально. Только в этом случае сверху перегородки должен находиться более легкий, а снизу — более тяжелый газ. Если газы по обе стороны перегородки тождественны, то диффузия также будет происходить. В этом случае она называется самодиффузией. Макроскопически самодиффузию наблюдать нельзя, так как из-за тождественности молекул она не может проявиться ни в каком макроскопическом явлении. Для наблюдения самодиффузии надо как-то «выделить» часть молекул газа. Практически это можно сделать, если вместо однородного газа взять смесь двух изотопов его, один из которых является радиоактивным. Можно также взять смесь двух различных газов (например, СО и N2), молекулы которых одинаковы по массе и практически имеют одинаковые размеры.
Допустим, что концентрации «отмеченных» молекул п 1и «немеченых» п 2меняются в направлении оси трубы. Примем эту ось за координатную ось X. Если общая концентрация частиц
,
и температура газа остаются постоянными, то будет постоянно и давление во всем газе. Поэтому макроскопическое движение в газе возникнуть не может, и перемешивание молекул возможно за счет одной только диффузии. Молекулы газа 1 и молекулы газа 2 будут диффундировать в противоположных направлениях — от мест большей концентрации к местам меньшей концентрации. Для количественного описания явления введем понятие диффузионного потока. Диффузионным потоком Г называется количество молекул рассматриваемого типа, проходящих при диффузии через единичную площадку, перпендикулярную к градиенту концентрации, в единицу времени. Задача теории диффузии сводится к вычислению диффузионных потоков.
Для вычисления потоков Г1 и Г2 обоих газов при самодиффузии можно воспользоваться формулой для переноса импульса
.
Роль «переносимой величины» g в этом случае играют относительные концентрации газов
, 
.
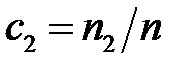Подставляя их в формулу для потока импульса, находим для диффузионного потока первого газа
.
Аналогичное выражение напишем для газа 2. Таким образом,
, 
.
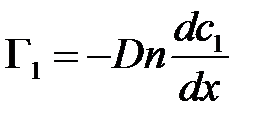Так как полная концентрация остается постоянной, то формулы можно также записать в виде
, 
.
Но если величина п не постоянна, а меняется в пространстве под действием какой-либо причины (например, силового поля или градиента температуры), то надо пользоваться более общими первыми формулами.
Из постоянства полной концентрации 
следует
,
а потому Г1 = –Г2.
Диффузионные потоки обоих газов одинаковы по величине, но направлены противоположно. Формулы 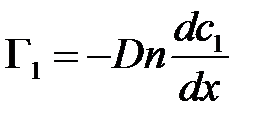, показывают, что диффузионный поток пропорционален градиенту концентрации. Это — закон Фика. Величина D называется коэффициентом диффузии. В случае самодиффузии он определяется выражением
.
Закон Фика справедлив и для взаимной диффузии различных газов. Однако здесь выражение для коэффициента диффузии , вообще говоря, неприменима. Ею можно пользоваться только в тех случаях, когда концентрация рассматриваемого газа очень мала по сравнению с концентрацией другого газа смеси. При выполнении этого условия средняя длина свободного пробега молекул рассматриваемого газа λ определяется столкновениями их только с молекулами другого газа смеси. Взаимные же столкновения между молекулами рассматриваемого газа, ввиду малости его относительной концентрации, роли не играют. Аналогичная ситуация встречается и при диффузии нейтронов в графите. Это явление используется для замедления нейтронов в ядерных реакторах. Ввиду малости концентрации нейтронов последние ведут себя как молекулы идеального газа, сталкивающиеся время от времени с ядрами атомов графита. Диффузия нейтронов хорошо описывается формулой . Длина свободного пробега нейтронов в графите порядка сантиметра.
Когда концентрации обоих газов в смеси одного порядка, то при построении теории концентрационной диффузии по методу средней длины свободного пробега надо вводить две средние длины свободного пробега: для молекул первого и второго газов. Эти длины свободного пробега являются характеристиками рассматриваемой смеси газов. Теория получается довольно громоздкой и плохо согласуется с экспериментом. Лучшие результаты дают теории, в которых понятие длины свободного пробега не используется. В следующих лекциях мы рассмотрим один из вариантов приближенных теорий такого типа, в основе которого лежит формула Эйнштейна.
12. Связь коэффициента диффузии с подвижностью частицы
Понятием подвижности используется для рассмотрения многих процессов, но смысл его всегда один и тот же. Например, при построении теории броуновского движения это понятие применялось к броуновским частицам, движущимся в жидкости под действием постоянных сил. На движущуюся в жидкости частицу действует сила сопротивления, пропорциональная скорости движения частицы. Подвижностью называется коэффициент этой пропорциональности:
.
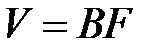Но оно применимо и к частицам молекулярных и атомных размеров, например к ионам, движущимся в электролите. На заряженный ион в постоянном электрическом поле действует постоянная сила F,пропорциональная напряженности электрического поля. Кроме того, при движении ион испытывает столкновения с окружающими молекулами и ионами. При отсутствии внешней силы F движение иона было бы полностью беспорядочным. При наличии постоянной силы F появляется преимущественное направление скорости иона. На беспорядочное тепловое движение накладывается регулярное движение в направлении силы F. Если электрическое поле не очень сильное, то установившаяся скорость иона пропорциональна приложенной к нему силе F. То есть в общем подвижностью частицы называется коэффициент пропорциональности В между регулярной скоростью и силой.
Допустим теперь, что имеется «газ» каких-то частиц в постоянном и однородном силовом поле. «Газ» настолько разрежен, что силами взаимодействия между его частицами можно полностью пренебречь. Примером такого «газа» может служить совокупность броуновских частиц, взвешенных в жидкости. Другим примером является обычный идеальный газ в силовом поле. Если F — сила, действующая на частицу «газа» в силовом поле, то потенциальная энергия ее в этом поле будет
.
(Предполагается, что ось X направлена в сторону действующей силы.) Если состояние стационарно, то концентрация частиц «газа» меняется в пространстве в соответствии с формулой Больцмана, которую можно получить из барометрических формул (давление в газе в поле силы тяжести, Универсальная газовая постоянная выражается через произведение постоянной Больцмана на число Авогадро):
, 
:
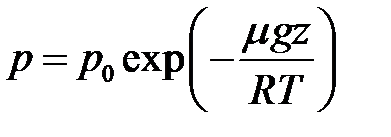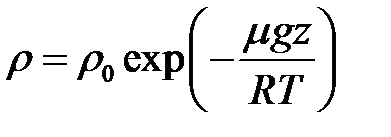Но микропроцессы не прекращаются даже тогда, когда состояние стационарно. Поскольку есть градиент концентрации, в газе происходит диффузия. Диффузионный поток в положительном направлении оси X определяется выражением
.
А так как «газ» находится в силовом поле, то существует также и «силовой поток» молекул с плотностью
.
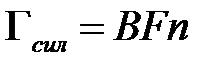В состоянии равновесия должно быть
.
Подставляя сюда распределение Больцмана, получаем после сокращения на n
.
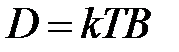Зто соотношение между коэффициентом диффузии и подвижностью частицы было установлено Эйнштейном и носит его имя.
