В жидкостях законы переноса имеют тот же вид, что и в газах:
закон Фурье: 
закон Фика: 
.
Коэффициент вязкости, описывающий внутреннее трение в жидкости, мы рассматривали ранее:
,
где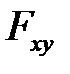 
– сила, необходимая, чтобы два слоя жидкости единичной площади, находящиеся на расстоянии dy, двигались в направлении x со скоростью по отношению друг к другу.
Целью данного раздела будет рассмотрение основных существующих подходов по расчету h, l, D для жидкости, исходя из представлений о ее молекулярной структуре. В виду сложности теорий, ограничимся лишь изложением их основных идей. При вычислении коэффициентов переноса используют подходы, основанные либо на близости жидкости к газу, либо к твердому телу. Мы рассмотрим и тот, и другой, а затем метод, не использующий такую аналогию и являющийся наиболее общим при расчете коэффициентов переноса в жидкости.
Из элементарных молекулярно-кинетических рассуждений известно, что для разреженного газа справедливы следующие выражения для коэффициентов переноса:
; (3.4)
; (3.5)
, (3.6)
где 
- длина свободного пробега; 
- плотность; m, d – масса и диаметр молекулы; n – среднечисловая плотность; СV – изохорная теплоемкость, 
- средняя тепловая скорость молекул, k – константа Больцмана.
Как известно, более строгая теория, основанная на уравнении Больцмана, уточняет числовые коэффициенты в уравнениях (3.4-3.6), не внося ничего принципиально нового.
Хотя коэффициенты переноса в жидкости и газе существенно различаются: 
, многие результаты кинетической теории газов для коэффициентов переноса используют и для жидкости. Например, рассмотрим коэффициент теплопроводности для жидкости. Будем считать, что для описания теплопроводности в жидкости справедлива формула 
. Из общей физики известно, что тепловая скорость примерно совпадает со скоростью звука в жидкости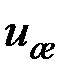 
, а изохорная теплоемкость в расчете на одну молекулу равна 3 k. Очевидно, что длина свободного пробега в жидкости пропорциональна корню третьей степени объема, приходящегося на одну частицу υ(объем же обратно пропорционален плотности n). В результате формулу (3.6) можно переписать в виде
(3.7)
Эта формула достаточно хорошо описывает поведение коэффициента теплопроводности, в частности его зависимость от температуры (как плотность, так и скорость звука обычно уменьшаются с увеличением температуры, соответственно коэффициент теплопроводности также уменьшается).
Несмотря на приведенный вывод, необходимо всегда помнить, что жидкость занимает промежуточное положение между газом и твердым телом, не только с точки зрения своей структуры и интенсивности межмолекулярных взаимодействий, но и с точки зрения теплового движения частиц. Так, в кристаллах наблюдаются в основном колебания возле определенных положений равновесия, в разреженных газах – беспорядочные, в основном парные столкновения, в жидкостях же наблюдается комбинация этих двух процессов.
Согласно представлениям, которые ввел Я. Френкель, тепловое движение атомов в жидкости можно представить как совокупность двух процессов:
1. Нерегулярных колебаний со средним периодом 
(близким к частотам колебаний атомов в кристаллических телах и равным 
с) и амплитудой, определяемой размерами “свободного объема”, предоставляемой ей ее соседями.
2. Перемещение частицы через некоторое время t в новое положение, вблизи которого она снова некоторое время колеблется. Время оседлой жизни t для обычных маловязких жидкостей составляет около 
с (оно увеличивается с повышением вязкости жидкости и, например, для стекол может быть порядка часов и суток).
Используя такую модель Френкеля, получим выражения для коэффициентов диффузии и вязкости. Пусть x - среднее межатомное расстояние в жидкости. В связи с большой плотностью частиц в жидкости и их сильным взаимодействием следует ожидать, что перемещение частиц на расстояние порядка x за время t будет совершаться преимущественно не в виде непрерывных перемещений, а в виде более или менее резких скачков с преодолением потенциального барьера U, разделяющего две возможные области. Как известно из статистической физики, вероятность такого скачка пропорциональна 
, а так как среднее время оседлой жизни частицы t обратно пропорционально вероятности перескока, то
. (3.8)
Далее используем две формулы, которые мы получали ранее:
1. Связь коэффициента диффузии со смещением частицы за некоторое время, используя введенные выше обозначения:
. (3.9)
2. Связь коэффициента диффузии броуновской частицы с ее подвижностью 1/ f:
, (3.10)
где f - коэффициент трения, для шарообразной броуновской частицы равный 
.
Используя выражения (3.8) и (3.9), получим
. (3.11)
Данный закон для коэффициента диффузии, полученный качественно, соответствует экспериментальным данным. Так, при повышении температуры коэффициент диффузии жидкости увеличивается (у газов было такое же поведение).
Для того чтобы получить формулу для коэффициента вязкости, будем считать, что приложенная постоянная внешняя сила к жидкости достаточно мала и она приводит к появлению преимущественно направленных скачков вдоль направления действия силы, но при этом частота скачков 1/ t не изменяется. Используя уравнения и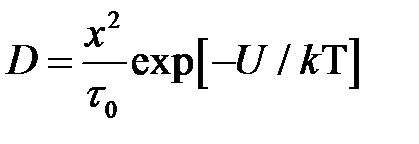 
, получим:
. (3.12)
Из проведенных качественных рассуждений следует, что с увеличением температуры вязкость уменьшается. Напомним, что у газов зависимость обратная. Это объясняется тем, что, в отличие от механизма внутреннего трения в газах, в которых передача импульса происходит за счет парных столкновений, главной причиной вязкости в жидкости (существенно более плотной среде) является существующие силы притяжения между молекулами. Так как импульс молекул газа с температурой увеличивается, то и вязкость увеличивается. В жидкости же при увеличении температуры расстояние между молекулами увеличивается и, следовательно, силы притяжения уменьшаются, что приводит к уменьшению коэффициента динамической вязкости.
