Допустим, что в газе распространяется параллельный пучок молекул. Это может быть внешний пучок, состоящий из молекул другого газа. Но пучок может состоять и из молекул того же газа. Можно представить себе, например, что в какой-то момент времени в газе отмечены молекулы с определенным направлением скорости. Пусть J 0 — интенсивность пучка (число частиц, проходящих через единичную площадку, перпендикулярную к пучку, в единицу времени), когда он пересекает плоскость АВ, перпендикулярную к нему. Найдем интенсивность J того же пучка на расстоянии х от плоскости AВ. Возьмем бесконечно тонкий слой газа с толщиной dx и площадью поперечного сечения S = 1. Число молекул газа в нем равно nSdx = ndx. Согласно определению эффективного сечения
, среднее число частиц, выбывающих из пучка из-за столкновений с одной молекулой газа, равно Jσ, а из-за столкновений с ndx молекулами 
. На такую величину уменьшится интенсивность пучка после прохождения слоя dx, а потому
.
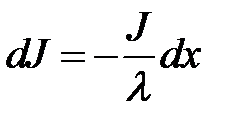Интегрируя это выражение, получим
.
Из-за рассеяния интенсивность пучка убывает экспоненциально. В связи с этим величину 1/ λ называют коэффициентом рассеяния. Согласно формуле 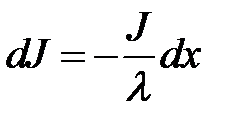величина dx/λ определяет вероятность рассеяния на пути dx, а 1/ λ — вероятность рассеяния на единице длины.
Формуле можно также дать следующее толкование. Если N 0 — число частиц, прошедших через площадку АВ, то число частиц, прошедших без столкновения расстояние х, определяется выражением
.
Число частиц, претерпевших столкновение в слое (х, х + dx), равно
.
Средний путь, пройденный частицами без столкновений, равен
.
Он, как и следовало ожидать, совпадает с длиной свободного пробега λ.
Формула применима также к другому случаю, существенному для излагаемой ниже элементарной теории явлений переноса. Представим себе, что в некоторый момент времени скорости всех молекул газа изменили направления на противоположные, но сохранили свои значения по величине. Такая замена не скажется на хаотичности движения молекул газа. Однако каждая молекула в точности повторит предшествующее движение, но в обратном направлении. Отсюда получается следующий результат. Пусть площадку АВ пересекло N 0 молекул, двигавшихся перпендикулярно к ней. Отметим все эти молекулы. На расстоянии х перед площадкой АВ число отмеченных молекул будет . По мере приближения к площадке АВ оно возрастает из-за столкновений. Число отмеченных молекул, претерпевших столкновения между х и х + dx, определяется прежним выражением
.
На формуле или основан прямой метод измерения длины свободного пробега. Этот метод был предложен и осуществлен М. Борном и Е. Борман в 1921 г.
Идея опыта состояла в следующем. Путем испарения получался пучок атомов серебра, резко ограниченный диафрагмами. На пути пучка помещались 4 коаксиальных диска на расстоянии 1 см друг от друга, в которых были вырезаны одинаковые круглые отверстия с центрами на оси системы. Через них и проходили атомы серебра. На каждом диске прикреплялся стеклянный квадрант, вершина которого лежала на оси системы. (На рис. 80 один из квадрантов изображен сбоку.) Квадранты были повернуты друг относительно друга на 90°, так что на каждый из них направлялась четвертая часть атомов пучка. Вся система помещалась в кварцевой трубке, давление воздуха в которой менялось с помощью насоса и измерялось манометром. Диски охлаждались жидким азотом. На пути от источника атомы серебра частично рассеивались молекулами воздуха, а затем конденсировались на квадрантах, стоящих на пути пучка. Пусть N 1, N 2, N 3, N 4 — числа атомов серебра, осевших на квадрантах. Тогда согласно формуле
должно выполняться
.
Аналогичные соотношения можно написать для каждой пары квадрантов. Отношение N 1/ N 2 можно было измерить по степени почернения стеклянных квадрантов, которая находилась путем фотометрирования. Затем, зная расстояние между дисками (х 2 – х 1), можно было найти и среднюю длину свободного пробега λ. Найденные таким путем значения λ удовлетворительно согласуются с результатами других методов, которые будут изложены ниже. Было показано также, что величина λ обратно пропорциональна давлению воздуха p в трубке? как это и требуется формулой 
.
Опыты Борна и Борман дают эффективное сечение рассеяния атомов серебра на молекулах воздуха. Более важным является случай, когда и пучок, и газ состоят из одинаковых молекул. Тогда средняя длина свободного пробега λ является характеристикой самого газа. Зная ее, можно вычислить эффективное поперечное сечение σ по формуле , а затем найти и газо-кинетический диаметр молекулы, связанный с σ соотношением 
. Именно таким путем впервые Лошмидтом (1821—1895) были определены геометрические размеры молекул.
Основные сведения о длинах свободного пробега были получены косвенными методами. Они основаны на изучении так называемых явлений переноса: внутреннего трения, теплопроводности и диффузии. С феноменологической точки зрения явление внутреннего трения мы рассматривали разделе механики жидкостей и газов. В следующих параграфах мы изложим эти явления, а также явление диффузии с молекулярно-кинетической точки зрения. Строгая молекулярно-кинетическая теория перечисленных явлений очень сложна. Она сводится к приближенным решениям так называемого кинетического уравнения Больцмана. Последнее является основным в кинетической теории газов. В принципе оно позволяет найти функцию распределения молекул газа по координатам и скоростям не только в состоянии равновесия, но и тогда, когда в газе происходят различные процессы. Однако уравнением Больцмана мы пользоваться не будем. При изложении внутреннего трения и теплопроводности газов мы изберем значительно более простой путь, использующий понятие средней длины свободного пробега.
