В термодинамически равновесных системах, как известно, температура Т и химический потенциал μ постоянны вдоль всей системы:
Если эти условия не выполняются (
), то в системе возникают необратимые процессы переноса массы, энергии, электрического заряда и т. д.
При обобщении классической термодинамики на неравновесные процессы исходят из представления о локальном равновесии. Известно, что время релаксации растет с увеличением размеров системы, так что отдельные макроскопически малые части системы приходят сами по себе в равновесное состояние значительно раньше, чем устанавливается равновесие между этими частями. Поэтому в неравновесной термодинамике принимают, что, хотя в целом состояние системы неравновесно, отдельные ее малые части равновесны (точнее, квазиравновесны), но имеют термодинамические параметры, медленно изменяющиеся во времени и от точки к точке.
Размеры этих физически малых равновесных частей неравновесной системы и времена изменения термодинамических параметров в них определяются в термодинамике экспериментально. Обычно принимается, что физический элементарный объем l 3, с одной стороны, содержит большое число частиц (v 0 < l 3, v 0— объем на одну частицу), а с другой стороны, неоднородности макроскопических параметров аi (r) на длине l малы по сравнению со значением этих параметров 
, т.е.
Время τ изменения термодинамических параметров в физически малых равновесных частях намного больше времени τl релаксации в них и намного меньше времени τL, за которое устанавливается равновесие во всей системе:
.
В условиях, когда допустимо такое представление о локальном равновесии, можно построить последовательную феноменологическую термодинамику необратимых процессов. Свойства неравновесной системы при этом определяются локальными изменениями по пространственным координатам и времени через характеристические термодинамические параметры, для которых справедливы уравнения термодинамики. Так, если в качестве характеристических переменных выбраны локальная плотность внутренней энергии 
, удельный объем 
) (
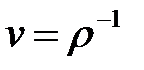, ρ – локальная плотность массы среды) и локальные концентрации 
различных компонентов, то состояние физически элементарного объема в окрестности точки r в момент времени t описывается локальной энтропией 
, определяемой уравнением Гиббса
(1)
Объединяющее первое и второе начала термодинамики уравнение (1) для удельных (по массе) локальных величин является основным уравнением неравновесной термодинамики. Так как локальная энтропия s (единицы массы или ρs – единицы объема) зависит от термодинамических параметров 
так же, как и при полном равновесии, то при необратимом процессе в адиабатной системе (теплоизолированная система, которая не обменивается с окружающей средой энергией в форме теплоты) скорость возникновения энтропии в единице объема (производство энтропии) равна
Рассматривая увеличение энтропии при изменении локальных макроскопических параметров аi в адиабатных условиях как ≪причину≫ необратимого процесса, величины 
называют термодинамическими силами, а величины 
, определяющие скорость изменения параметров аi – термодинамическими потоками. Выражение для производства энтропии с такими определениями можно записать в виде
.
Энтропия всей неравновесной системы аддитивно складывается из энтропий ее отдельных частей:
.
