Основы теории процессов переноса.
Механика жидкости.
1. Давление жидкости. Распределение давление в покоящейся жидкости (гидростатика). Закон Паскаля. Закон Архимеда
2. Барометрическая формула.
3. Движение жидкости (методы описания движения жидкости, линия тока, трубка тока, стационарное и нестационарное течение, условие неразрывности потока). Уравнение Бернулли.
4. Формула Торричелли. Задача о вытекании жидкости из сосуда. Кавитация. Форма струи жидкости.
5. Вязкость. Движение жидкости между вращающимися коаксиальными цилиндрами.
6. Стационарное течение жидкости по прямолинейной трубе. Формула Пуазейля.
7. Турбулентность и гидродинамическая неустойчивость (общее представление пример с неустойчивостью течения при движении жидкости между вращающимися коаксиальными цилиндрами).
Явления переноса в газах.
8. Средняя длина свободного пробега.
9. Эффективное сечение.
10. Распределение молекул по длинам свободного пробега.
11. Внутреннее трение и теплопроводность газов. Уравнение Фурье для теплопроводности.
12. Самодиффузия в газах. Уравнение Фика.
13. Связь коэффициента диффузии с подвижностью частицы.
14. Концентрационная диффузия в газах.
15. Броуновское движение как процесс диффузии.
16. Термическая диффузия в газах.
17. Нестационарные уравнения переноса в газах. Времена релаксации.
18. Явления в разреженных газах. Вакуум. Теплопередача при малых давлениях. Диффузия при малых давлениях. Трение при малых давлениях. Сосуды, сообщающиеся через пористую перегородку. Эффузия газа. Эффект Кнудсена.
Описание явлений переноса в жидкостях.
19. Теплопроводность и диффузия в жидкостях. Подходы описания, основанные на подобии жидкости газу. Модель Френкеля.
20. Кинетические коэффициенты в жидкости с точки зрения решеточной модели жидкости.
Исходные положения неравновесной термодинамики.
21. Локальное равновесие и основное уравнение термодинамики неравновесных процессов. Термодинамические силы и потоки.
22. Уравнения баланса и законы сохранения различных величин.
23. Линейный закон. Соотношения взаимности Онсагера и принцип Кюри.
24. Термомеханический и механокалорический эффекты.
Давление жидкости. Закон Паскаля. Закон Архимеда
Жидкости в отличие от твердых тел не имеют собственной формы и не сопротивляются деформации сдвига. Поэтому они способны изменять свою форму под действием сколь угодно малых сил. Сложнее изменить объем жидкости. Если под действием внешнего воздействия происходит изменение объема, в жидкости возникают упругие силы, в конце концов, уравновешивающие внешнее воздействие. Упругие свойства жидкостей проявляются в том, что отдельные части их действуют друг на друга или на соприкасающиеся с ними тела с силой, зависящей от степени сжатия. Это воздействие характеризуется величиной, называемой давлением.
Рассмотрим жидкость, находящуюся в равновесии (то есть когда отдельные части жидкости не перемещаются относительно друг друга или относительно граничащих с ними тел). Выделим мысленно в жидкости площадку ∆ S. Соприкасающиеся на этой площадке части жидкости действуют друг на друга с равными по величине и противоположно направленными силами. чтобы выяснить характер этих сил, мысленно удалим часть жидкости с одной стороны площадки и заменим ее действие силами такой величины и направления, чтобы не нарушалось равновесие оставшейся жидкости. Очевидно, что эта сила должны быть нормально направленной к ∆ S, так как иначе тангенциальная составляющая этих сил привела бы жидкость в движении, а нам нужно сохранить равновесие. Следовательно, и равнодействующая ∆ f всех сил, действующих, с которыми на эту площадку действует жидкость, также направлена по нормали к этой площадке. И если эту силу ∆ f отнести к единице поверхности площадки, то получим величину, называемую давлением.
Таким образом, давление можно определить как
 .
.
Эта формула справедлива для равномерно распределенной силы. Если же сила распределена не равномерно, мы переходим к давлению в точке, для этого устремляя ∆S к нулю:

Силы давления жидкости всегда перпендикулярны к соответствующим поверхностям (дну сосуда, боковой поверхности и т.д.). Давление жидкости – СФВ, так как величина его в данной точке не зависит от ориентации площадки ∆ S, к которой отнесено давление. На первый взгляд может показаться удивительным, что пропорциональное векторной величине (силе) давление оказывается скалярной величиной. Однако, следует иметь в виду, что площадка ∆ S также может рассматриваться как вектор, имеющий направление нормали к ∆ S, то есть мы можем задавать ориентацию площадки в пространстве. Следовательно, давление представляет собой отношение двух коллинеарных векторов, а такая величина, как известно, представляет собой скаляр.
В условиях равновесия жидкости, как правило, сжаты (собственным весом), но могут быть и растянуты (например, висящая капля, жидкость сопротивляется разрыву). В последнем случае силы, действующие внутри объема жидкости, называю натяжением или отрицательным давлением. Такие силы внутри объема жидкости, как правило приводят к нарушению сплошности среды.
Вообще говоря, сжимаемость жидкости мала, и поэтому во многих случаях изменением объема жидкости полностью пренебрегают. Малую сжимаемость жидкостей часто демонстрируют с помощью следующего опыта. Сосуд из пластмассы (деревянный ящик, бумажный пакет) наполняют жидкостью, но не полностью. Если выстрелить по этому сосуду так, чтобы пуля прошла выше уровня жидкости, то она оставит лишь отверстие в стенках сосуда, сам сосуд остается целым. Но если выстрел пройдет ниже уровня жидкости, то сосуд разлетится вдребезги. Причина в том, что когда пуля попадает в жидкость, она должна либо сжать ее на величину своего объема, либо вытеснить этот объем жидкости наверх. Но для вытеснения не достаточно времени. Происходит сжатие – в жидкости развиваются большие давления, которые и разрывают стенки сосуда. Аналогичные явления возникают при разрывах глубинных бомб, применяемых против подводных лодок. Вследствие малой сжимаемости воды при разрыве бомбы возникают большие давления, которые и разрушают лодку.
Однако следует иметь в виду, что в ряде задач сжимаемость жидкости приходится учитывать, например, при изучении распространения звуковых волн в жидкости.
Распределение давление в покоящейся жидкости (гидростатика). Если бы в жидкости не было объемных сил (например, в невесомости), то условием равновесия было бы постоянство давления во всем объеме. Это одна из формулировок закона Паскаля. Также можно сказать который гласит, что в жидкостях и газах силы давления одинаковы по всем направлениям. Т.е. они передают производимое на них давление одинаково по всем направлениям. Этот закон был установлен экспериментальным путем.
Продемонстрировать это можно следующим образом. Выделим в жидкости небольшой произвольно ориентированный цилиндрический объем высотой ∆ l и основанием ∆ S. Если бы в точках на расстоянии ∆ l друг от друга давление отличалось бы на величину ∆ p, то вдоль оси цилиндра действовала бы сила ∆ p ∆ S, что привело бы жидкость в движение и равновесие было бы нарушено. Следовательно, при отсутствии объемных сил в состоянии равновесия в любом месте жидкости должно выполняться условие  , откуда следует, что ∆ p =const.
, откуда следует, что ∆ p =const.

Рассмотрим распределение давления при наличии объемных сил (поскольку мы говорим о покоящейся жидкости, то единственной объёмной силой может быть собственный вес жидкости). Выделим в жидкости объем в виде горизонтального цилиндра с малым сечением.

Поскольку объёмная сила направлена по вертикали, вдоль оси цилиндра будут действовать только две силы: p 1∆ S и p 2∆ S. Как мы видели раньше, из условия равновесия вытекает, что p 1 = p 2, значит, во всех точках, лежащих в одной горизонтальной плоскости, давление будет одинаковым.
Теперь выделим цилиндрический объем жидкости с малым сечением таким образом, чтобы его ось была вертикальна.

В этом случае, кроме сил давления на основания будет действовать также объемная сила  . Условие равновесия (вспомним, что жидкость должна покоиться) в этом случае будет иметь вид
. Условие равновесия (вспомним, что жидкость должна покоиться) в этом случае будет иметь вид
 ,
,
 .
.
Таким образом, давление на двух разных уровнях в жидкости отличается на величину, численно равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равной единице. Эту добавку называют гидростатическим давлением. Из формулы видно, что от формы жидкости гидростатическое давление не зависит. Если столб жидкости не вертикальный, то высота отсчитывается по вертикали от рассматриваемой точки до уровня свободной поверхности жидкости. (Пример с наклоненным цилиндром, рисунок.)
Кроме того, в расчетах также необходимо учитывать внешнее давление, действующее на поверхность жидкости. оно характеризует сжатие жидкости под действием внешней силы, действующей перпендикулярно поверхности жидкости. В качестве внешнего часто выступает атмосферное давление.
Закон Архимеда.
Следствием неодинаковых давлений на разных уровнях жидкости является наличие выталкивающей силы. Она действует на тела, погруженные в жидкость, со стороны жидкости действует и называется силой Архимеда. Рассмотрим пример.
Возьмем тело произвольной формы, полностью погруженное в жидкость, и найдем силу, действующую на это тело со стороны жидкости. Для этого разобьем тело на объемы с малыми элементарными площадками dS 1 и dS 2, вырезаемыми на поверхности тела. (вертикальные столбики).
 Рис.
Рис.
Силы, действующие на эти площадки, нормальны к ним и равны соответственно p 1 dS 1 и p 2 dS 2. Спроецируем эти силы на вертикальную ось, в результате получим:
 ,
,
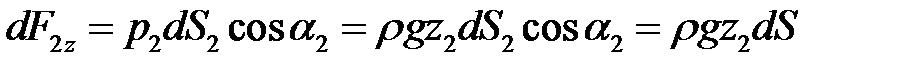 ,
,
где  – площадь нормального сечения выделенного объема.
– площадь нормального сечения выделенного объема.
Суммарная сила, действующая вдоль оси z, будет равна:
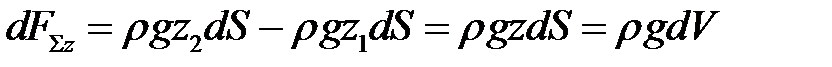 .
.
Интегрируя по всему объему тела, получим суммарную силу гидростатического давления, действующую на тело (сила Архимеда):
 .
.
Если тело плавает в жидкости, то легко показать, что в эту формулу будет входить объем погруженной части тела. (Показать самостоятельно, это будет на зачете.)
Рассмотрим, к какой части тела приложена эта сила и куда она направлена. Чтобы ответить на этот вопрос необходимо вспомнить условия равновесия твердого тела. Одним из таких условий является равенство нулю суммы моментов сил, действующих на тело. На плавающее тело действуют две силы – сила тяжести и сила Архимеда. Рассмотрим моменты этих сил относительно оси, проходящей через центр тяжести тела. Поскольку сила тяжести проходит через центр тяжести, то она не создает вращательного момента для тела. Следовательно, и сила Архимеда не должна создавать вращательного момента. Но это возможно только тогда, когда эта сила приложена к центру тяжести тела (в случае полного погружения тела). Направлена она должна быть вверх.
Если тело погружено не полностью, то сила Архимеда будет приложена к так называемому центру плавучести, который является центром масс вытесненного объема жидкости (ее ось проходит через центр тяжести).
В итоге, можно сформулировать закон Архимеда. Если тело, погруженное в жидкость, удерживается в механическом равновесии, то со стороны окружающей жидкости оно подвергается выталкивающей силе гидростатического давления, численно равной весу жидкости в объеме, вытесненном телом. Эта выталкивающая сила направлена вверх и проходит через центр масс жидкости, вытесненной этим телом.
Барометрическая формула.
Теперь рассмотрим гидростатику сжимаемой жидкости. Одним из самых интересных примеров является равновесие земной атмосферы. Для этого нам понадобится дифференциальное уравнение, так называемое основное уравнение гидростатики.
Силы, действующие в жидкости, обычно разделяют на массовые (объемные) и поверхностные. Массовая сила пропорциональна массе dm, а с ней и объему dV элемента жидкости, на который она действует. Эту силу можно обозначить как f dV, где f выступает в роли объемной плотности массовой силы. Важнейшими примерами таких сил являются сила тяжести, когда f = ρ g и силы инерции (в неинерциальных системах отсчета). К поверхностным силам относятся силы, которым подвергается каждый объем жидкости благодаря касательным и нормальным напряжениям, действующим на его поверхности со стороны окружающих его частей жидкости.
Когда жидкость покоится, в ней действуют только нормальные давления, о которых мы говорили ранее. Выделим в жидкости бесконечно малый объем dV и найдем действующую на него равнодействующую силу давления. У той силы будет три проекции. Сначала рассмотрим проекцию на горизонтальную ось. Выберем объем в виде горизонтального цилиндра с основанием dS и длиной dx.

На основания, как мы уже видели, действуют силы давления p (x) dS и p (x+dx) dS. Мы указали, что давление зависит от координаты x и ее приращения, но эта функция, естественно, может зависеть и от координат y, z, а также от времени. Но при переходе от одного основания к другому эти аргументы не меняются в силу малости выбранного элемента объема, поэтому могут считаться постоянными. На боковую поверхность цилиндра действует сила давления, перпендикулярная оси цилиндра, поэтому в искомую составляющую вклад не дает. Таким образом, горизонтальная проекция силы давления, равна
 .
.
Эта разность является бесконечно малой, поэтому мы можем перейти к дифференциалу функции, 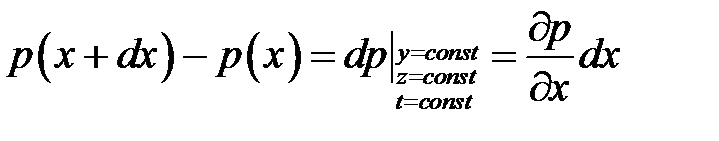 .
.
Тогда для силы получим
 .
.
Видим, что эта сила пропорциональна элементу объема dV, и ее можно обозначить sxdV, где sx – горизонтальная составляющая силы, действующей на единицу объема жидкости, которая возникает из-за изменения нормального давления в пространстве, причем она не зависит от формы рассматриваемого элемента объема. Аналогично можно получить проекции этой силы на две оставшиеся оси. в итоге имеем
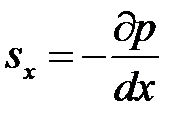 ,
,  ,
,  ,
,
или 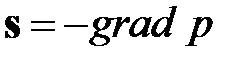 .
.
В состоянии равновесия эта сила должна уравновешиваться массовой силой f, что приводит к уравнению
 .
.
Это уравнение и является основным уравнением гидростатики. Если жидкость находится в поле сил тяжести, то f = ρg. Тогда уравнение гидростатики примет вид
 ,
,  .
.
Оба эти уравнения выведены без предположения о несжимаемости жидкости, поэтому воспользуемся ими для рассмотрения равновесия земной атмосферы. Первые два уравнения можно не учитывать, так как они говорят только о том, что давление не зависит от высоты. Оставшееся третье уравнение можно переписать в виде полного дифференциала
 .
.
В этом уравнении две неизвестные функции – давление и плотность. Значит, чтобы найти давление, нам нужно дополнительное условие.
Будем предполагать, что состав атмосферы один и тот же на всем ее протяжении. Если газ не слишком плотный, то можно воспользоваться уравнением состояния, а именно, уравнением Клапейрона
 ,
,
где μ – молекулярный вес газа. Исключаем из уравнения гидростатики плотность, получая в итоге
 ,
,
Мы заменили неизвестную плотность на неизвестную температуру, но ее уже легче измерить на разных высотах.
Если отсутствуют ветры и воздушные течения, то атмосфера неподвижна и находится в состоянии механического равновесия. Но для полного равновесия необходимо еще тепловое равновесие. А это означает, что температура должна быть одинаковой на протяжении всей атмосферы. Такое состояние газа или жидкости называется изотермическим. Конечно, это идеализация, но тем не менее полученные в такой модели результаты вполне применимы на практике. При T = const наше уравнение легко интегрируется и в результате получаем
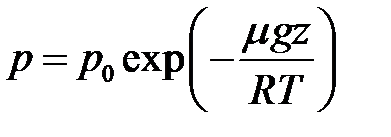 .
.
По этому же закону меняется и плотность изотермической атмосферы
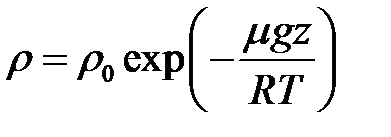 .
.
Эти два соотношения называются барометрическими формулами. Постоянные интегрирования имеют смысл давления и плотности воздуха на поверхности земли






