Рассмотрим основополагающие правила комбинаторики – правила суммы и произведения.
Пусть Х – конечное множество, состоящее из n элементов x. Тогда говорят, что элемент x из X может быть выбран n способами и пишут 
. Эта запись совпадает с записью мощности множества X.
Пусть 
– попарно непересекающиеся множества, т.е. 
, 
.
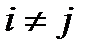Очевидно, что в этом случае
.
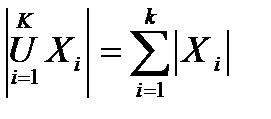Таково комбинаторное правило суммы. Для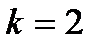 
оно формулируется следующим образом. Если объект x может быть выбран n способами из множества X, а объект y из непересекающегося с ним множества Y – другими m способами, то выбор «x или y» может быть осуществлён 
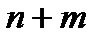способами.
Правило произведения для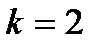 
формулируется следующим образом. Если объект x может быть выбран n способами и после каждого из таких выборов объект y в свою очередь может быть выбран m способами, то выбор упорядоченной пары – вектора 
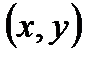– может быть осуществлён 
способами, например, 
, 
.
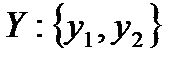Тогда упорядоченные пары 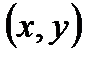описываются декартовым произведением:
.
Выбор упорядоченной последовательности из k объектов вектора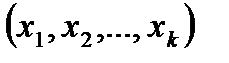 
может быть осуществлён 
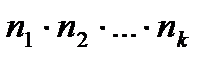– способами, где ni – число способов выбора i -го объекта xi, i меняется от 1 до k (записывается: 
).
В частности, если все ni равны, что может быть, например, в случае, когда элементы принадлежат одному и тому же множеству, т.е. рассматривается декартово произведение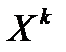 
, то число способов равно 
.
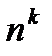Размещения
Пусть задано некоторое конечное множество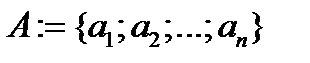 
– генеральная совокупность. Из элементов генеральной совокупности образуются выборки 
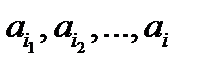, где 
.
Выборки классифицируются следующим образом:
в зависимости от того, существенен порядок элементов выборки или нет, её называют упорядоченной или неупорядоченной;
в зависимости от того, могут или не могут элементы выборки повторяться, её называют выборкой сповторениями или выборкой без повторений.
Число элементов выборки называют её объёмом. Выборку объёма r называют r -выборкой.
Размещением из n элементов по m называется упорядоченная m -выборка из n -элементной генеральной совокупности.
Пример. Даны три буквы – a, b, c. Размещения из трех элементов (букв) по два в каждом:
(a, b), (b, a), (a, c), (c, a), (b, c), (c, b).
Если говорить о размещениях с повторениями, то к этому списку добавится еще три:
.
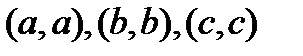Число размещений из n элементов по m без повторений обозначают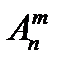 
, а с повторениями 
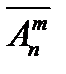. Например, 
.
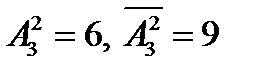Получим общие формулы для числа размещений. Если элементы размещения не могут повторяться, то число способов, каким можно выбрать каждый очередной элемент размещения, будет на единицу меньше, чем для предшествующего ему, а так как первый элемент размещения выбирается n способами, то с помощью правила произведения получаем формулу
.
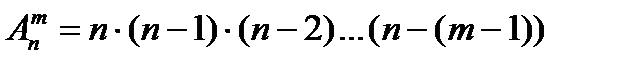В размещении с повторениями каждый очередной элемент может быть выбран n способами, поэтому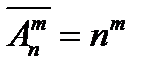 
.
Число размещений можно еще вычислить по формуле
. 
Разделим и умножим эту формулу на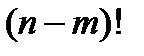 
, получим
;
. 
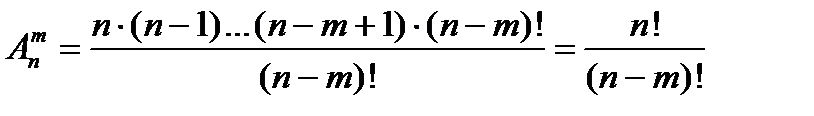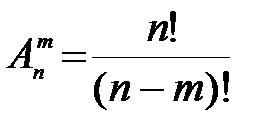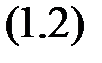
Сочетания
Сочетанием из n элементов по m называют неупорядоченную m -выборку из n элементов генеральной совокупности. Выборки отличаются только составом элементов, порядок следования их не учитывается.
Пример: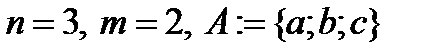 
.
Выпишем всевозможные сочетания из трех букв по две (без повторений):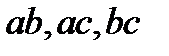 
.
Если говорить о сочетаниях с повторениями, то к этому списку добавится еще три: 
.
Число сочетаний из n по m -элементам обозначают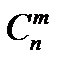 
, а с повторениями 
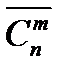, например 
, 
.
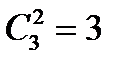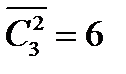Выведем формулу для 
. Всякое размещение можно получить как произведение сочетания на перестановку:
;
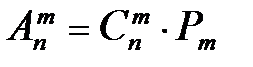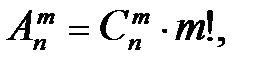
откуда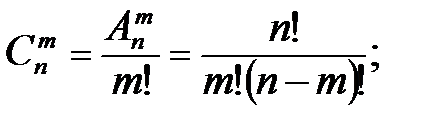 
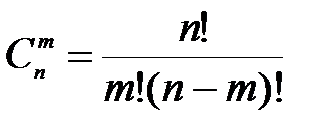. (1.3)
Сочетания с повторениями
Закодируем сочетания с повторениями последовательностью из нулей и единиц следующим образом: сначала запишем столько единиц, сколько раз в сочетание входит первый элемент исходного множества, затем – 0, затем столько единиц, сколько раз в сочетание входит второй элемент исходного множества, затем 0 и т.д. После единиц, соответствующих повторению последнего элемента, 0 не ставим.
Пример. Пусть n =3, m =5. Исходное множество a, b, c – n =3. Сочетания с повторениями из пяти элементов, например:
aaabc – кодировка 1110101;
abbbb – кодировка 1011110;
ccccc – кодировка 0011111.
Заметим, что в кодирующей последовательности ровно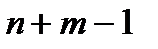 
элементов 
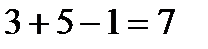, m – единиц (столько, сколько элементов в сочетании) и 
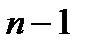нулей (отделяющих друг от друга n наборов единиц, соответствующих n элементам исходного множества). Очевидно, что любой последовательности такого вида соответствует некоторое сочетание с повторениями из n по m.
Пример: n =3, m =5; a, b, c; последовательности 1110011 соответствует ааасс, а 0111110 – bbbbb.
Таким образом, установлено взаимно-однозначное соответствие между множеством сочетаний из n по m и множеством последовательностей из m единиц и 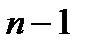нулей. Число этих последовательностей равно 
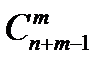или 
. Это соответствие: 
.
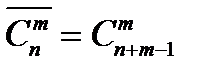Примеры задач на сочетания с повторениями
1.Каким числом способов можно разместить n одинаковых шаров по k различным урнам?
Решение. Присвоим урнам номера от 1 до k. Будем считать, что, помещая шар в урну, мы присваиваем ему её номер. Тогда размещение шаров по урнам сводится к построению последовательности, в которой n элементов, и каждый из них принимает одно из k значений. Таким образом, ответ к задаче –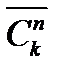 
:
. 
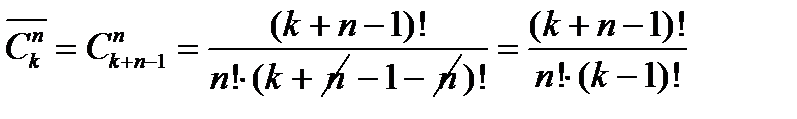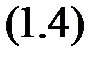
2. Найти число решений уравнения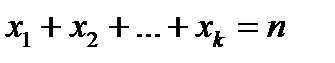 
в неотрицательных целых числах.
Решение. Задача опять сводится к числу распределений одинаковых шаров по различным урнам, если считать, что xi – количество шаров, помещаемых в i -ю урну, n – общее число шаров, k – общее число урн. Ответ: 
.
Перестановки
Перестановки – это частный случай размещения, когда n=m, т.е.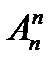 
.
В выборке элементы отличаются только порядком следования, состав элементов – одинаковый. Обозначается Pn. По формуле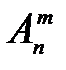 
при n=m (0!=1) число перестановок равно:
Рn = n!.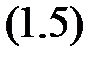 
Комбинаторные тождества
В ниже перечисленных соотношениях значения параметров предполагается такими, чтобы все биномиальные коэффициенты имели смысл. Если в формуле присутствует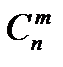 
, то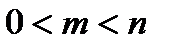 
.
Имеют места следующие тождества:
1. 
.
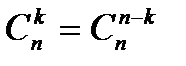2. 
.
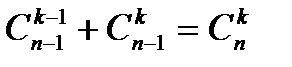3. 
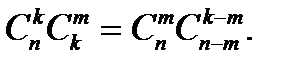
4. 
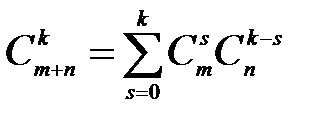– свертка Вандермонда.
