Два высказывания называются равносильными, если равны их истинностные функции, рассматриваемые как функции от всех значений переменных, т.е. на каждом наборе значений оба высказывания принимают одинаковые значения.
Основные равносильности:
1. Коммутативность.
а) 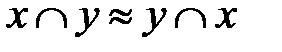 (для конъюнкции);
(для конъюнкции);
б)  (для дизъюнкции).
(для дизъюнкции).
2. Ассоциативность.
а) 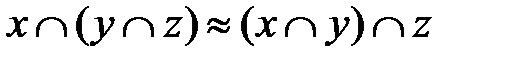 (для конъюнкции);
(для конъюнкции);
б)  (для дизъюнкции).
(для дизъюнкции).
3. Дистрибутивность.
а)  (для конъюнкции относительно дизъюнкции);
(для конъюнкции относительно дизъюнкции);
б)  (для дизъюнкции относительно конъюнкции).
(для дизъюнкции относительно конъюнкции).
4. Закон де Моргана.
а) ┐  ┐
┐ 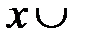 ┐
┐  (отрицание конъюнкции есть дизъюнкция отрицаний);
(отрицание конъюнкции есть дизъюнкция отрицаний);
б) ┐ 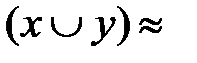 ┐
┐  ┐
┐ 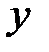 (отрицание дизъюнкции есть конъюнкция отрицаний).
(отрицание дизъюнкции есть конъюнкция отрицаний).
5. Идемпотентность.
а)  (для конъюнкции);
(для конъюнкции);
б)  (для дизъюнкции).
(для дизъюнкции).
6. Поглощение.
 .
.
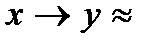 ┐
┐ 
7. Расщепление (склеивание).
а)  (1–ый закон расщепления);
(1–ый закон расщепления);
б) 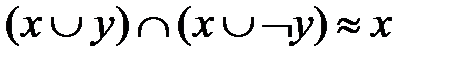 (2–ой закон расщепления).
(2–ой закон расщепления).
8. Двойное отрицание.
┐┐х=х
9. Свойства констант.
а) 
б) 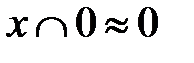
в) 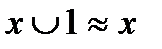
г) 
д) 
е)  .
.
10. Закон противоречия.

11. Закон “исключенного третьего”.

Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа “  ”. Докажем, например, равносильность 4а. Для этого составим таблицу.
”. Докажем, например, равносильность 4а. Для этого составим таблицу.
Таблица
| х | у | 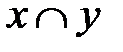
| 
| 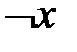
| 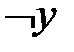
|  Ø Ø
|
Из таблицы видно, что  º
º  Ø, что и требовалось доказать.
Ø, что и требовалось доказать.
Прямая, обратная и противоположная теоремы
Рассмотрим четыре теоремы:
 , (1) , (1)
 , (2) , (2)
|  , (3) , (3)
 . (4) . (4)
|
Определение 1: Пара теорем, у которых условие одной является заключением второй, а условие второй является заключением первой, называются взаимно обратными друг другу.
Так, теоремы (1)и (2), а также (3) и (4)- взаимно обратные теоремы. При этом, если одну из них называют прямой теоремой, то вторая называется обратной.
Определение 2: Пара теорем, у которых условие и заключение одной являются отрицанием соответственно условия и заключения другой, называются взаимно противоположными.
Так, теоремы (1) и (3), а также (2) и (4) являются взаимно противоположными теоремами.
Например, для теоремы
“Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником ” (1) обратной является теорема
“Если четырехугольник является прямоугольником, то его диагонали равны” (2).
Для теоремы (1) противоположной является теорема
“Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольником” (3),
а для теоремы (2) противоположной является теорема
“Если четырехугольник не является прямоугольником, то его диагонали не равны ” (4).
В рассмотренном примере теоремы (1) и (4) являются одновременно ложными, а теоремы (2) и (3) одновременно истинными. Контрпримером к теореме (1) является равнобочная трапеция.
Ясно, что прямая и обратная теоремы, вообще говоря, не равносильны, т. е. одна из них может быть истинной, а другая – ложной. Однако легко показать, что теоремы (1) и (4), а также (2) и (3) всегда равносильны.
Действительно:
 Из этих равносильностей следует, что, если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3).
Из этих равносильностей следует, что, если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3).




