В пространстве каждая его точка 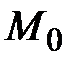 (рис. 35) представляется тремя декартовыми координатами: абсциссой
(рис. 35) представляется тремя декартовыми координатами: абсциссой 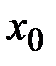 , ординатой
, ординатой 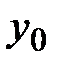 и аппликатой
и аппликатой 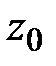 (записывается
(записывается 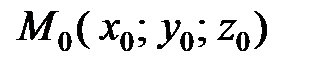 ). Точка также может быть задана своим радиус-вектором
). Точка также может быть задана своим радиус-вектором
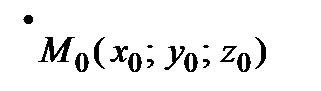
|

|

|

|
|

|

|
| Рис. 35 |

|
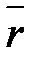
|

|
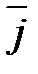
|
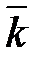
|
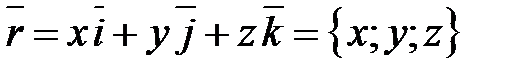 ,
,
проведенным из начала координат в эту точку.
Расстояние 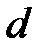 между точками пространства
между точками пространства 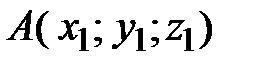 и
и 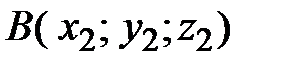
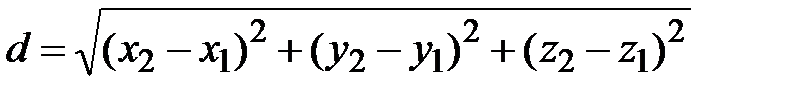 ;
;
координаты середины отрезка 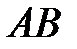 :
:
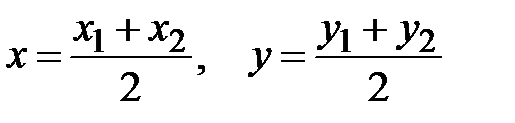 ,
, 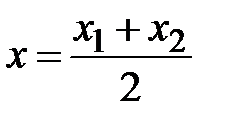
Уравнение вида
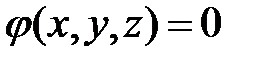 или
или 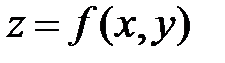 (26)
(26)
 связывающее координаты
связывающее координаты 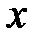 ,
,  и
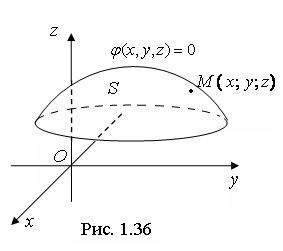
и 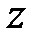 точек пространства, называется уравнением поверхности
точек пространства, называется уравнением поверхности 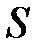 , если:
, если:
a)
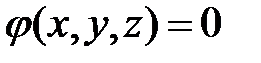
|
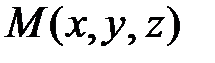 поверхности
поверхности 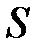 удовлетворяют этому уравнению (рис. 1.36);
удовлетворяют этому уравнению (рис. 1.36);
b) координаты любой точки, не лежащей на поверхности 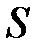 , неудовлетворяют этому уравнению.
, неудовлетворяют этому уравнению.
Уравнение (26) в общем случае задает в пространстве некоторое точечное множество, которое может быть и не поверхностью в пространстве.
Пример. Уравнение 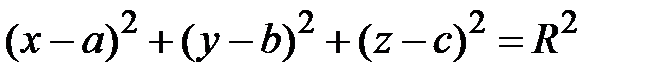 есть уравнение шара радиуса
есть уравнение шара радиуса 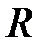 с центром в точке с координатами
с центром в точке с координатами 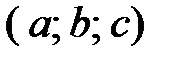 ; уравнение
; уравнение 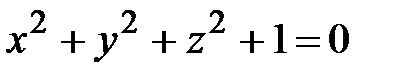 не задает ни одной точки в пространстве (его решением является пустое множество).
не задает ни одной точки в пространстве (его решением является пустое множество).
Значения координат 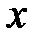 ,
,  , и
, и 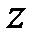 , которые удовлетворяют системе уравнений двух поверхностей
, которые удовлетворяют системе уравнений двух поверхностей
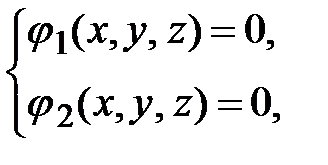
определяют линию пересечения этих поверхностей. Если система не имеет решений, то поверхности не пересекаются.
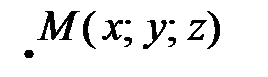
|
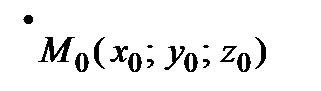
|
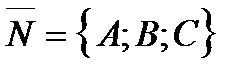
|
| Рис. 37 |
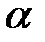
|
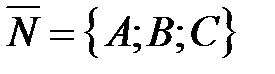 – любой вектор, перпендикулярный данной плоскости
– любой вектор, перпендикулярный данной плоскости 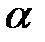 (нормальный вектор плоскости), а
(нормальный вектор плоскости), а 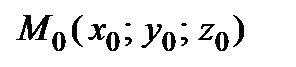 – точка, через которую плоскость проходит (рис. 37). Любой вектор
– точка, через которую плоскость проходит (рис. 37). Любой вектор 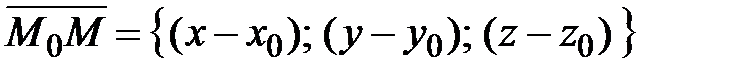 , проведенный из точки
, проведенный из точки 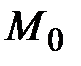 в произвольную точку плоскости
в произвольную точку плоскости 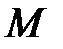 , будет перпендикулярен вектору
, будет перпендикулярен вектору 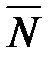 и, следовательно, их скалярное произведение
и, следовательно, их скалярное произведение 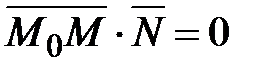 , т. е.
, т. е.
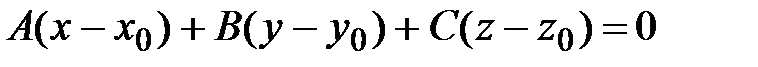 .(27)
.(27)
Полученное уравнение есть уравнение плоскости, проходящей через заданную точку 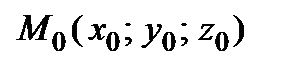 плоскости перпендикулярно заданному вектору
плоскости перпендикулярно заданному вектору 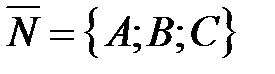 . Оно первой степени относительно декартовых прямоугольных координат (линейно).
. Оно первой степени относительно декартовых прямоугольных координат (линейно).
Уравнение (27) можно переписать в виде
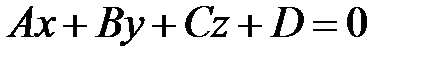 или
или 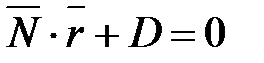 (28)
(28)
где 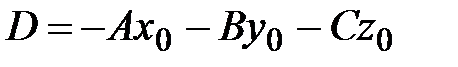 . Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при
. Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при 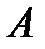 ,
, 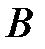 и
и  не равных нулю одновременно оно определяет плоскость с нормальным вектором
не равных нулю одновременно оно определяет плоскость с нормальным вектором 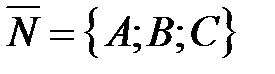 . Обратно, каждую плоскость можно определить уравнением первой степени относительно декартовых прямоугольных координат вида (28).
. Обратно, каждую плоскость можно определить уравнением первой степени относительно декартовых прямоугольных координат вида (28).
Пример. Составить уравнение плоскости, проходящей через точку 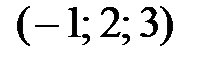 параллельно плоскости
параллельно плоскости 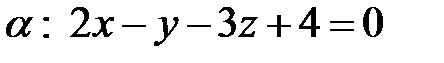 .
.
◄ Так как искомая плоскость 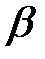 параллельна плоскости
параллельна плоскости 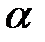 , для нее можно взять в качестве нормального вектора нормальный вектор плоскости
, для нее можно взять в качестве нормального вектора нормальный вектор плоскости 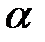 :
: 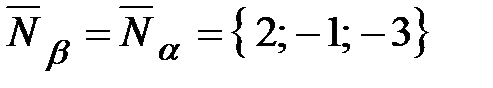
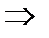
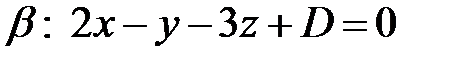 . Величину
. Величину 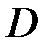 найдем из условия, что искомая плоскость проходит через точку
найдем из условия, что искомая плоскость проходит через точку 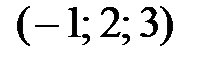 , т. е. координаты этой точки должны удовлетворять уравнению плоскости:
, т. е. координаты этой точки должны удовлетворять уравнению плоскости: 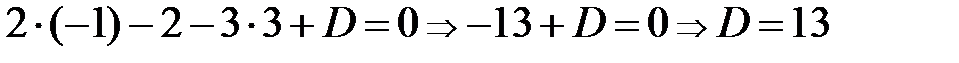 . Окончательно, искомое уравнение плоскости
. Окончательно, искомое уравнение плоскости 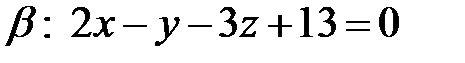 . ►
. ►
Особые случаи положения плоскости относительно системы координат, задаваемых общим уравнением (28):
1) 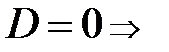 плоскость
плоскость 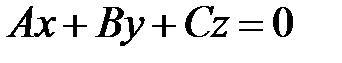 , проходящая через начало координат;
, проходящая через начало координат;
2) 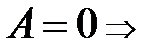 плоскость
плоскость 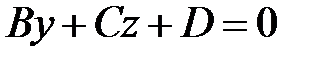 параллельна оси
параллельна оси 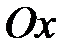 (оси
(оси 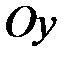 при
при 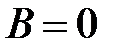 , оси
, оси 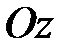 при
при 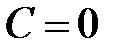 );
);
3) 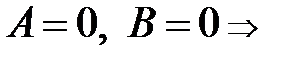 плоскость
плоскость 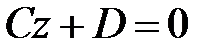 параллельна координатной плоскости
параллельна координатной плоскости 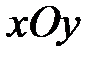 (
(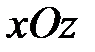 при
при 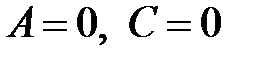 ,
, 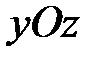 при
при 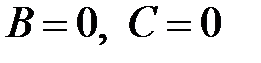 );
);
4) 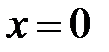 – уравнение координатной плоскости
– уравнение координатной плоскости 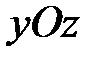 (
(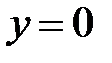 –
– 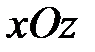 ,
, 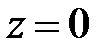 –
– 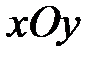 ).
).
Уравнение плоскости в зависимости от решаемой задачи может быть задано в различных формах.

|

|

|
|
| Рис. 38 |
|
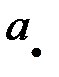
|
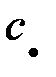
|
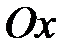 в точке
в точке 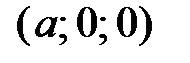 , ось
, ось 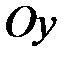 в точке
в точке 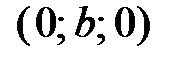 и ось
и ось 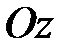 в точке
в точке 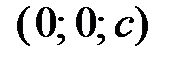 (рис. 38) имеет уравнение (уравнение плоскости в отрезках)
(рис. 38) имеет уравнение (уравнение плоскости в отрезках)
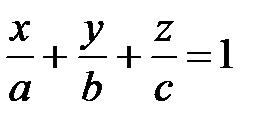 . (29)
. (29)
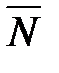
|

|

|

|
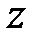
|
| Рис. 39 |

|
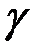
|

|
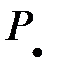
|
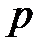 – расстояние плоскости от начала координат (длина перпендикуляра
– расстояние плоскости от начала координат (длина перпендикуляра 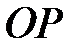 , опущенного из начала координат на плоскость) (рис. 39),
, опущенного из начала координат на плоскость) (рис. 39), 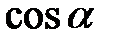 ,
, 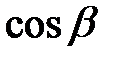 ,
, 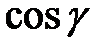 – направляющие косинусы нормального вектора
– направляющие косинусы нормального вектора 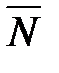 :
: 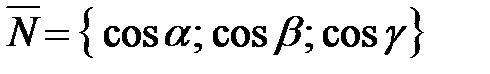 , длина
, длина 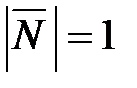 , т. к.
, т. к. 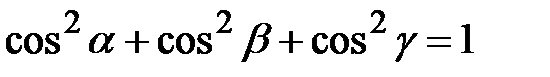 . Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)
. Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)
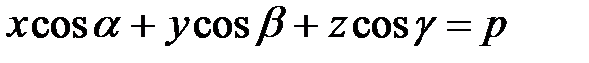 . (30)
. (30)
Уравнение плоскости, проходящей через три данные точки 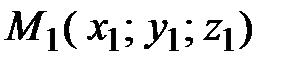 ,
, 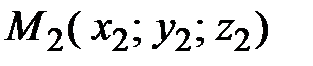 ,
, 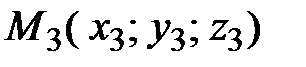 , не лежащие на одной прямой, имеет вид
, не лежащие на одной прямой, имеет вид
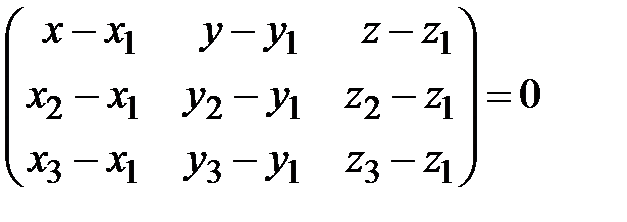 . (31)
. (31)
Пример. Составить уравнение плоскости, проходящей через точки 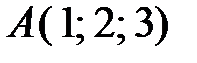 ,
, 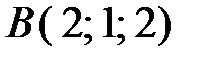 и
и 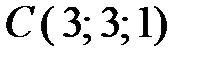 .
.
◄ Подставляя координаты данных точек в формулу (31), будем иметь 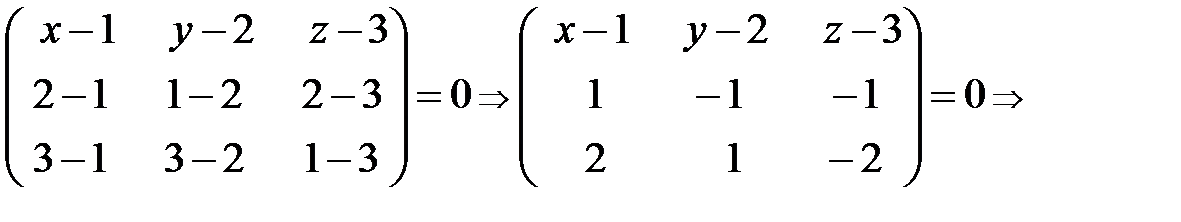
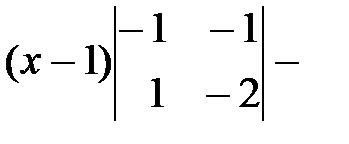
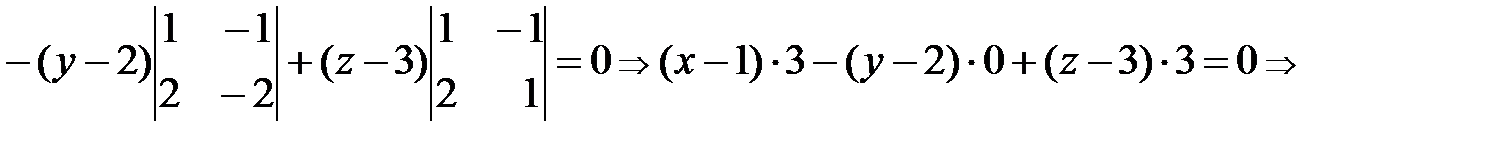
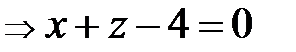 . Так как в полученном уравнении плоскости нет слагаемого с координатой
. Так как в полученном уравнении плоскости нет слагаемого с координатой 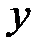 , делаем вывод, что она параллельна оси
, делаем вывод, что она параллельна оси 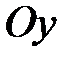 . ►
. ►
Прямая в пространстве
Система двух линейных уравнений
| Рис. 40 |
|
|
|
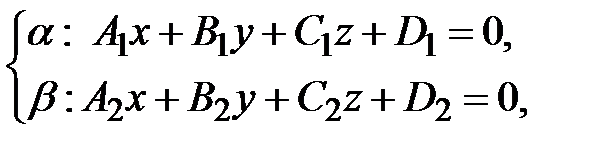 (32)
(32)
определяет прямую 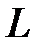 как пересечение двух плоскостей
как пересечение двух плоскостей 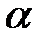 и
и 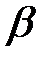 (рис. 40) при условии, что эти плоскости не параллельны
(рис. 40) при условии, что эти плоскости не параллельны 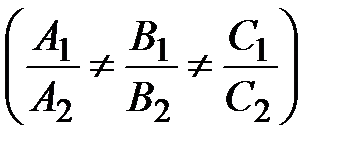 . При
. При 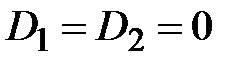 (и только в этом случае) прямая проходит через начало координат.
(и только в этом случае) прямая проходит через начало координат.

|

|

|
|
| Рис. 1.41 |
|
|
|
Пример. Рассмотрим систему 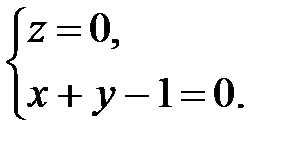 . Первое уравнение системы задает координатную плоскость
. Первое уравнение системы задает координатную плоскость 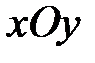 , а второе – плоскость, параллельную оси
, а второе – плоскость, параллельную оси 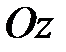 . Пересечение этих плоскостей дает прямую линию, лежащую в координатной плоскости
. Пересечение этих плоскостей дает прямую линию, лежащую в координатной плоскости 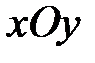 (рис. 41).
(рис. 41).
| Рис. 42 |
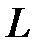
|
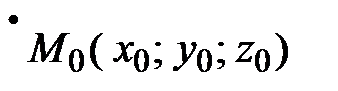
|
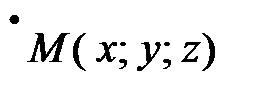
|
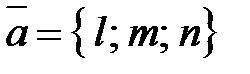
|
Если прямая проходит через точку 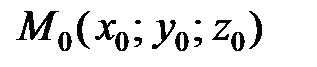 параллельно вектору
параллельно вектору 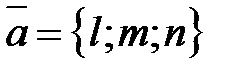 (направляющий вектор прямой), то из условия
(направляющий вектор прямой), то из условия 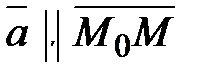 , где
, где 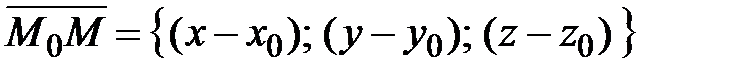 – вектор, проведенный из точки
– вектор, проведенный из точки 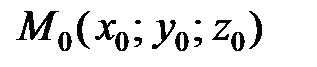 в произвольную точку прямой
в произвольную точку прямой 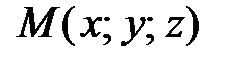 (рис. 42), получаем канонические уравнения прямой:
(рис. 42), получаем канонические уравнения прямой:
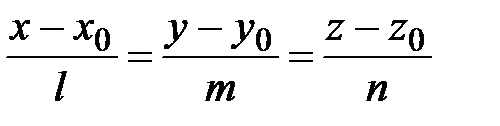 (33)
(33)
Уравнения прямой, проходящей через две точки 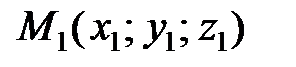 и
и 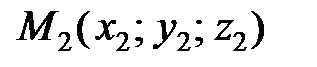 , следуют из (33), если в качестве направляющего вектора прямой взять вектор
, следуют из (33), если в качестве направляющего вектора прямой взять вектор 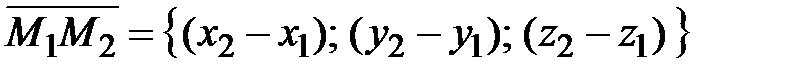 и одну из двух точек (все равно какую), через которые прямая проходит:
и одну из двух точек (все равно какую), через которые прямая проходит:
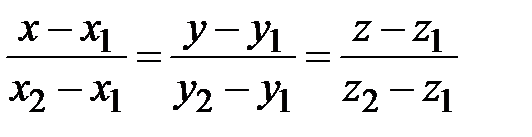 (34)
(34)
Направляющий вектор 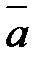 прямой, заданной как линия пересечения двух плоскостей (системой (32)), может быть получен при помощи векторного произведения нормальных векторов
прямой, заданной как линия пересечения двух плоскостей (системой (32)), может быть получен при помощи векторного произведения нормальных векторов 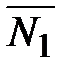 и
и 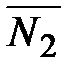 этих двух плоскостей:
этих двух плоскостей:
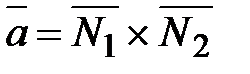 . (35)
. (35)
Обозначив в канонических уравнениях (33) отношение через 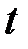 (
(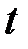 – переменный параметр), получаем параметрические уравнения прямой в пространстве:
– переменный параметр), получаем параметрические уравнения прямой в пространстве:
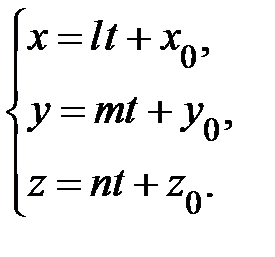 (36).
(36).
Пример. Составить параметрические уравнения прямой 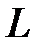 , заданной как пересечение двух плоскостей
, заданной как пересечение двух плоскостей 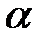 и
и 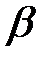 :
: 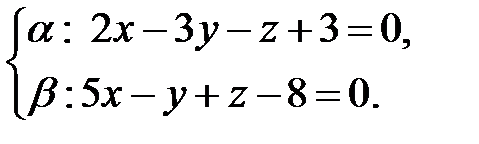 .
.
◄ Направляющий вектор прямой 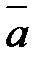 найдем по формуле (35) при
найдем по формуле (35) при 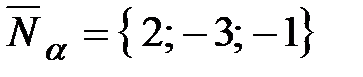 ,
, 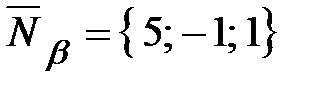 :
: 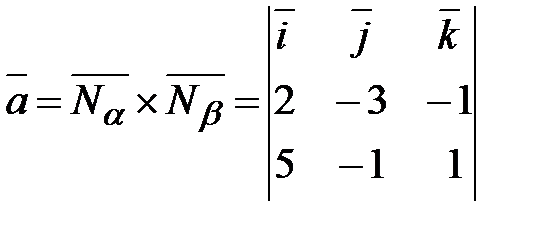 =
= 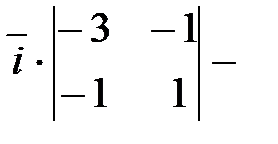
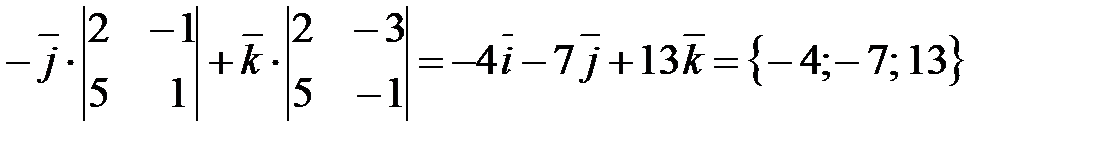 . Произвольную точку, через которую проходит прямая, можно найти, положив одну из ее координат любому значению и решив затем получающуюся из исходной системы систему двух уравнений с двумя остающимися неизвестными координатами точки. Положив
. Произвольную точку, через которую проходит прямая, можно найти, положив одну из ее координат любому значению и решив затем получающуюся из исходной системы систему двух уравнений с двумя остающимися неизвестными координатами точки. Положив 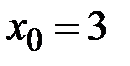 , получаем систему
, получаем систему 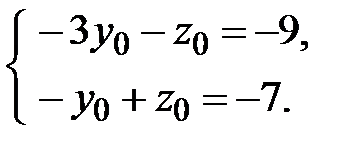 . Решение этой системы:
. Решение этой системы: 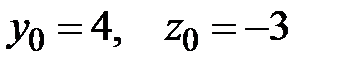 , т. е. прямая проходит через точку с координатами
, т. е. прямая проходит через точку с координатами 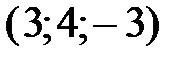 . Подставив эти координаты и координаты направляющего вектора в (36), получаем искомые уравнения прямой:
. Подставив эти координаты и координаты направляющего вектора в (36), получаем искомые уравнения прямой: 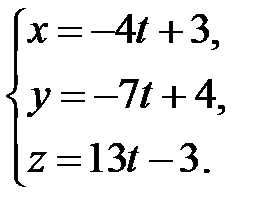 . ►
. ►
3 Линии (кривые) второго порядка на плоскости






