Множество - это совокупность, класс отличающихся друг от друга объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества.
Множества обозначаются заглавными буквами латинского алфавита, а элементы множества- строчными.
Примеры множеств:
Классы (множества) чисел: N – натуральные числа, Z – целые числа, Q- рациональные числа, R- действительные (вещественные) числа, C – комплексные числа.
Студенты одной группы – множество, элементы которого- студенты, общее свойство – обучение одной специальности.
Множество В – корни уравнения ½ = cosx. Элементы – вещественные числа, общее свойство – обращают данное уравнение в верное равенство.
Если х – элемент множества Х, то говорят: х принадлежит Х и пишут: хÎХ. Если х не принадлежит Х, то пишут хÏХ.
Виды множеств: конечные множества, бесконечные, пустые, универсальные.
Конечные и бесконечные множества в свою очередь подразделяются на неупорядоченные и упорядоченные; неупорядоченные бесконечные – на счетные и несчетные.
Рассмотрим два основных способа задания неупорядоченных множеств:
1. перечисление всех его элементов;
2. описание характеристического (общего) свойства его элементов.
Первым способом задаются конечные множества.
Примеры:
А – множество чисел, являющихся делителями числа 20: А = {1, 2, 4, 5, 10, 20}.
В – список группы: В = {Архипов, Белов,…}.
Вторым способом можно задать конечные множества, бесконечные, пустые. Множество элементов, обладающих характеристическим свойством Р, обозначается {x | P(x)} и читается так: множество всех х таких, что х обладает свойством Р(х).
Примеры:
{x | x ÎR, x2 – 4 = 0} - это конечное множество и его можно задать перечислением элементов: {2, -2};
{x | x Î R, 2< x < 5 } – бесконечное несчетное множество, а именно, числовой промежуток (2, 5);
{x | x Î R, 1= sinx} – бесконечное счетное множество;
{x | x Î R, x2 + 9 = 0 } – это пустое множество, т.к. ни одно вещественное число не удовлетворяет данному уравнению.
Отношения между множествами
Рассмотрим отношения между неупорядоченными множествами.
Если каждый элемент множества А принадлежит множеству В, то А называют подмножеством множества В.
Обозначения: А Í В (А принадлежит В, А включено в В, А содержится в В и т.д.), В Ê А (В включает А, В содержит А и т.д.)
Множества А и В называются равными, если А Í В и В Í А.Обозначение: А = В.
Если А Í В и существует хотя бы один элемент множества В, не принадлежащий множеству А, то А – собственная часть В, т.е. А строго включается в В.Обозначение: А Ì В.
Примеры:
N – множество натуральных чисел, М – множество четных чисел, тогда М Ì N.
Пусть Х – множество студентов группы, У – множество студентов данной группы сдавших экзамен, тогда можно построить отношение У Í Х, т.к. возможно, что все студенты успевающие.
А = {1, 3, 5, 10}, B = {10, 1, 1, 5, 3, 5}. Данные множества равны А = В, действительно: А Í В и В Í А.
Если U – универсальное множество некоторой теории, то любое множество этой теории является его подмножеством. Например, множество комплексных чисел С – универсальное множество в теории чисел. Для всех классов чисел можно построить цепочку включений: N Ì Z Ì Q Ì R Ì C.
Свойства включений:
1. Для всякого множества В: В Í В;
2. Для любых множеств А, В, С, если А Í В и В Í С, то А Í С;
3. Для всякого множества В: Æ Í В.
Операции над множествами
Над множествами можно выполнять действия (операции), напоминающие сложение и умножение чисел. Но не тождественные им.
Объединением (суммой) множеств А и В называется множество, обозначаемое через АÈВ, содержащее те и только те элементы, которые принадлежат множеству А или В. Краткая запись: АÈВ = {x | xÎ A или хÎ В}.
Соответствующая диаграмма Эйлера – Венна:
| А |
| В |
Пример: А = {2, 5, 7, 9}, В = {3, 5, 8, 9, 12}.
АÈВ = {2, 5, 7, 9 }È{3, 5, 8, 9, 12}= {2, 5, 7, 9, 3, 8, 12}.
Соответствующая диаграмма:
| 2, 7 |
| 5, 9 |
| 3, 8, 12 |
| А |
| В |
Пересечением (произведением) множеств А и В называется множество, обозначаемое через АÇВ и состоящее из тех и только из тех элементов, которые принадлежат множеству А и множеству В. Краткая запись: АÇВ = {x | xÎA и хÎВ}.
Соответствующая диаграмма Эйлера- Венна:
| А |
| В |
| АÇВ – заштрихованная область |
Пример: АÇВ= {2, 5, 7, 9 }Ç{3, 5, 8, 9, 12}= {5,9}.
| 2, 7 |
| 3, 8, 12 |
| 5, 9 |
Разностью множеств А и В называется множество, обозначаемое через А\В и состоящее из тех и только из тех элементов, которые принадлежат А и не принадлежат В. Краткая запись: А\В = {x| xÎ A и xÏB}.
Соответствующая диаграмма Эйлера- Венна:
| А |
| В |
| А\В- заштрихованная область |
Если U – универсальное множество и АÍ U, то разность U\A называется дополнением множества А до множества U и обозначается  .
.
Краткая запись:  = {x| xÎU и xÏA}.
= {x| xÎU и xÏA}.
| U |
| A |

|
Симметрической разностьюмножеств А и В называется множество, обозначаемое АDВ и состоящее из тех и только из тех элементов, которые принадлежат А\В или В\А. Краткая запись: ADB= {x| xÎA\B или xÎB\A}.
Соответствующая диаграмма Эйлера- Венна:

Законы алгебры множеств
1. Коммутативность 
2. Ассоциативность 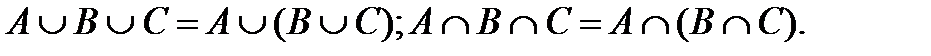
3. Дистрибутивность 
4. Закон поглощения 
5. Законы де Моргана 

Комбинаторика
Комбинаторика – раздел математики, изучающий способы решения задач пересчета и перечисления элементов в конечных множествах. Задача перечисления состоит в выделении элементов, принадлежащих некоторому заданному конечному множеству и удовлетворяющих некоторым свойствам, а задача пересчета – в нахождении числа таких элементов.
Задача. Описать все расположения 8 одинаковых ладей на шахматной доске, при которых ладьи не бьют друг друга.
Это задача перечисления. Если бы в этой задаче требовалось найти количество указанных расположений, то эта задача была задачей пересчета. Обычно речь в подобных задачах идет о комбинациях некоторых объектов, поэтому такие задачи называют комбинаторными.




