В качестве численной характеристикой доли утраченного здоровья или трудоспособности рассмотрим число 
из отрезка [0, 1] где ноль соответствует абсолютно здоровому человеку, а единица – полной потере здоровья. Некоторое значение 
, 
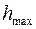, этой характеристики соответствует такой степени потери трудоспособности, при которой приходится переводить работника на менее вредное производство. Так как измерения доли утраченной трудоспособности субъективный характер, то принятие решения о переводе работника на менее вредное производство или инвалидность является случайным, и вероятность принятия такого решения монотонно зависит от реальной доли Z утраченной трудоспособности.
Процесс ухудшения здоровья и утраты трудоспособности человека, работающего на производствах с вредными и/или опасными условиями труда, можно описывать самыми разными способами, из которых далее рассматриваются два вида: детерминированная последовательность чисел из отрезка [0,1] и известные нам цепи Маркова с дискретным временем, множеством состояний которой является совокупность чисел от 0 до 1.
Чтобы учитывать ситуации, когда ухудшение состояния здоровья приводит (по самым случайным причинам) либо к инвалидности или смерти работника, либо к необходимости его перевода на работу с менее вредными условиями и выплаты в связи с этим периодической компенсации потери заработка вплоть до выхода на досрочную пенсию, имеет смысл дополнить величину Z, характеризующую состояние здоровья, дискретной компонентой, определяющей состояние работника: остается он на основном (вредном) производстве, переведен ли на менее вредное производство, переведен на пенсию по инвалидности и тому подобное. Параметры такой модели зависят от самого характера производства и выбираются в соответствии с имеющимися статистическими данными.
Изменения численной характеристики здоровья, как в детерминистической, так и в вероятностной моделях отражает следующие особенности:
а) доля утраченного здоровья естественно увеличивается с возрастом;
б) характер вредных/опасных условий труда определяет специфическую совокупность накапливающихся повреждений организма и характерный для каждого вида производства уровень утраты здоровья за заданное время работы, обусловленный самими условиями труда (без учета ситуаций полной потери трудоспособности);
в) при малой доле утраченного здоровья восстановительные и компенсационные возможности организма еще велики, и утрата здоровья и работоспособности происходит медленнее, чем при умеренной доле утраченного здоровья;
г) если характер вредных воздействий условий труда существенно влияет лишь на часть органов и подсистем организма, то при приближении к предельному для данного производства уровню скорость увеличения утраты здоровья уменьшается; аналогично, процесс утраты здоровья может также замедляться к старости в связи с замедлением всех процессов в организме;
д) вероятность наступления инвалидности и/или необходимости перевода на работу с пониженным уровнем вредности условий труда естественно возрастает с увеличением доли утраты здоровья.
Теперь введем следующие обозначения:
Zt – числовая характеристика доли утраченной трудоспособности после каких то t лет работы при вредных и/или опасных условиях (как отмечалось, 0 £ Zt £ 1),
b – естественный уровень утраты трудоспособности за один год в связи с увеличением возраста, обусловливающий среднюю утрату трудоспособности около 35% к моменту выхода на пенсию по старости в 55–60 лет,
p – степень утраты трудоспособности за один год, обусловленный вредными/опасными условиями труда.
Обозначим также через q перев(t) и q вых(t) соответственно вероятности того, что в течение года работник, у которого стаж работы с вредными или опасными условиями труда равен t, в связи с ухудшением состояния здоровья переведен на менее вредную работу вследствии чего возникнет необходимость в расходовании средств страхового фонда на компенсацию потери заработка или, что он получит право на пенсию по инвалидности или умрет (в обоих случаях он выходит из системы рассматриваемого вида страхования).
В модели выбрана прямая зависимость этих вероятностей от стажа работы, как наиболее часто встречающиеся, а не от уровня утраты трудоспособности. Такой подход практически исключает неизбежную субъективность в определении уровня утраты трудоспособности и упрощает оценку этих параметров по статистическим данным. Динамику параметров q перев(t) и q вых(t) можно использовать для обнаружения существенных изменений в уровне вредности и опасности условий труда.
Можно построить много различных математических моделей, в той или иной мере соответствующих описанным нами выше особенностям процесса утраты здоровья. Ниже описаны только две: детерминистическая и вероятностная.
В обеих моделях предполагается, что существует некий объективный уровень Wt повреждений подсистем организма за t лет работы при вредных условиях труда. Поэтому величина Wt ежегодно увеличивается в соответствии с интенсивностями b и p, но медицинские измерения Zt последствий этих повреждений чаще всего описываются нелинейной функцией h (x), которая принимает значения из отрезка [0, 1] и медленно растет при малых и больших уровнях повреждений: Zt = h (Wt).
Чтобы учесть отмеченное выше замедление влияния вредных и опасных условий труда на трудоспособность Zt, влияние параметра p компенсируется неким коэффициентом, уменьшающимся при увеличении стажа работы на производстве с вредными или опасными условиями труда. В качестве такого коэффициента в модели выбрана функция max{0,1 – t / T }, где t – стаж работы на производстве с вредными и (или) опасными условиями труда, а T – величина, которая никак не меньше максимально возможного времени работы при таких условиях. Иначе говоря, средний уровень влияния вредных и (или) опасных условий труда на величину Wt на t -м году стажа считается в модели равным (1 – t / T) p при t < T и равным 0 при t ≥ T.
В детерминистической же модели уравнения в этом случае принимают вид
Zt = h (Vt), Vt +1 = Vt + b + p (0,1 – t / T), t =0,1,… T. (141)
Выбирая подходящий аналитический вид функции h (x) и значения параметров b, p и T, можно получать желаемый нами вид зависимости величины Zt от параметра t.
Так, например, по статистическим данным, приближенные оценки уровня трудоспособности в зависимости от возраста и условий труда имеют следующий вид (см. Табл.27):
Таблица 27.
Зависимость уровня трудоспособности (значения 1 – Z) от возраста и условий труда[5]
| Возраст | Условия труда | ||
| Благоприятные | Список № 2 | Список № 1 | |
| 1 = 100% | 0,95 = 95% | 0,9 = 90% | |
| 0,55 = 55% | |||
| 0,55 = 55% | |||
| 0,65 = 65% | |||
| 0,3 = 30% | 0,25 = 25% | 0,2 = 20%; |
Численные расчеты показали, что очень близкие результаты получаются в математической модели при нелинейной функции
, (142)
T = 40, b = 0,018 и p = 0 для благоприятных условий труда:
Vt благ = 0,018 max(0, t – 25), Zt благ = h (Vt благ) (143)
(предполагается, что в 25 лет человек практически здоров), p = 0,009 для списка № 2:
Vt (2) = Vw благ + 0,018 max(0, t – 25) + 0,009 t (1 – t /(2 T)), Zt (2) = h (Vt (2)), (144)
где w – возраст поступления на работу с вредными и (или) опасными условиями труда, и p = 0,014 для списка № 1:
Vt (1) = Vw благ + 0,018 max(0, t – 25) + 0,0014 t (1 – t /(2 T)), Zt (1) = h (Vt (1)), (145)
Графики функции Zt (145) при этих значениях параметров приведены ниже на рис. 129.
Рис.129. Зависимость утраты трудоспособности от возраста и условий труда в математической модели.
Численные значения этих функций Zt при этих параметрах, соответствующие таблице 27, приведены в таблице 28.
Таблица 28.
Зависимость уровня утраты трудоспособности (значения Zt) от возраста и условий труда в математической модели
| Возраст | Условия труда | ||
| Благоприятные | Список № 2 | Список № 1 | |
| 0,025 | 0,06 | 0,09 | |
| 0,182 | 0,354 | 0,450 | |
| 0,277 | 0,459 | 0,547 | |
| 0,378 | 0,546 | 0,620 | |
| 0,684 | 0,759 | 0,789 |
Формулы для кусочно линейных приближений функций, изображенных на Рис.129 и в таблице, имеют следующий вид (см. Табл. 29):
Таблица 29.
Приближенные формулы для зависимости уровня утраты трудоспособности (значения Zt) от возраста и условий труда в математической модели при начале работы в 20 лет
| Возраст t | Условия труда | ||
| Благоприятные | Список № 2 | Список № 1 | |
| От 20 до 30 | 0,004 | 0,004+0,005(t –20) | 0,004+0,01(t –20) |
| От 30 до 45 | 0,004+0,006(t –30) | 0,054+0,015(t –30) | 0,104+0,021(t –30) |
| От 45 до 60 | 0,094+0,013(t –45) | 0,279+0,008(t –45) | 0,419+0,001(t –45) |
Аналогичные формулы для уровня утраты трудоспособности в зависимости от стажа и класса условий труда также имеют похожий аналитический вид, но параметры подбираются в соответствии со статистическими данными[6], согласно, которым, степени утраты трудоспособности после 30 лет занятости составляют:
для класса 3.2 25-30%
для класса 3.3 30-35%
для класса 3.4 35-40%
для класса 4 40-50%
Параметры модели (1) – (2), соответствующие этим данным, приведены ниже в таблице 30:
Таблица 30.
| Класс условий труда | b | p | T |
| 3.2 | 0,018 | 0,005 | |
| 3.3 | 0,018 | 0,008 | |
| 3.4 | 0,018 | 0,010 | |
| 0,018 | 0,016 |
Значениям параметров из этой таблицы соответствуют следующие формулы
Vt (3.2) = 0,018 max(0, w + t – 25) + 0,005 t (1 – t /(2 T)), Zt (3.2) = h (Vt (3.2)), (146)
Vt (3.3) = 0,018 max(0, w + t – 25) + 0,008 t (1 – t /(2 T)), Zt (3.3) = h (Vt (3.3)), (147)
Vt (3.4) = 0,018 max(0, w + t – 25) + 0,01 t (1 – t /(2 T)), Zt (3.4) = h (Vt (3.4)), (148)
Vt (4) = Vw благ + 0,018 max(0, w + t – 25) + 0,016 t (1 – t /(2 T)), Zt (4) = h (Vt (4)), (149)
Графики наблюдаемых нами функций Zt, которые соответствуют таким значениям параметров, приведены на рис. 130.
Рис.130. Зависимость утраты трудоспособности от возраста и классов условий труда в математической модели.
Аналогичные приближенные формулы для различных классов условий труда приведены в Таблице 31.
Таблица 31.
Приближенные формулы для зависимости уровня утраты трудоспособности (значения Zt) от возраста и классов условий труда в математической модели при начале работы в 20 лет
| Возраст t | Классы условий труда | ||
| 3.2 | 3.3 | 3.4 | |
| От 20 до 30 | 0,004+0,001(t –20) | 0,004+0,002(t –20) | 0,004+0,004(t –20) |
| От 30 до 45 | 0,014+0,010(t –30) | 0,024+0,014(t –30) | 0,044+0,016(t –30) |
| От 45 до 55 | 0,164+0,012(t –45) | 0,234+0,008(t –45) | 0,284+0,006(t –45) |
| От 20 до 27 | 0,004+0,006(t –20) | ||
| От 27 до 35 | 0,046+0,012(t –27) | ||
| От 35 до 50 | 0,142+0,013(t –35) |
Тогда в аналогичной вероятностной модели
Zt = h (Vt), Vt +1 = Vt + bt + pt max{0,1 – t / T }, (150)
функция h имеет тот же вид (1.2), но коэффициенты bt и pt (t = 0,1,…) являются независимыми случайными величинами отражающими влияние увеличения возраста, условий жизни и вредных и (или) опасных условий труда.
Распределения bt и pt можно выбирать произвольно, исходя из статистических данных и естественных предположений. Например, математические ожидания bt и pt должны соответствовать значениям параметров b и p в детерминистической модели, а дисперсии соответствовать статистическим данным и априорным соображениям. Тогда и характеристики утраты здоровья Vt и Zt также становятся случайными величинами. Случайные величины Vt представляют собой суммы независимых случайных величин, и их распределения можно будет вычислять с помощью стандартных методов теории вероятностей, а распределения Zt получаются из распределений Vt функциональными преобразованиями.
В этой модели моментом τ наступления страхового события – перевода работника на работу с меньшим уровнем вредности или получения права на досрочную пенсию – является наименьшее целочисленное значение аргумента 
, при котором значение Zt превышает заданный критический уровень .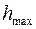
Для компенсации последствий наступивших профессиональных рисков для пострадавших на производстве требуется проводить и оплачивать медицинское лечение, медицинскую, социальную и профессиональную реабилитацию, оплачивать компенсационные выплаты (пенсии и пособия), включая досрочные пенсии; а также финансово обеспечивать выплаты пособий иждивенцам, лиц погибших вследствие несчастного случая на производстве (см. Рисунок 131).
Рисунок 131. Структура и пороговые значения профессионального риска и виды страховой защиты
1 - смертельные исходы (из-за производственного травматизма и профессиональной заболеваемости)
2, 3, 4 - постоянная утрата общей трудоспособности, включая: инвалидный исход: первой группы инвалидности (2), второй группы инвалидности (3), третьей группы инвалидности (4);
5 – постоянная утрата общей трудоспособности из-за производственного травматизма и профессиональной заболеваемости без инвалидного исхода, но с установлением степени утраты трудоспособности;
6 - постоянная утрата общей трудоспособности из-за производственного травматизма и профессиональной заболеваемости без установления степени утраты трудоспособности;
7– постоянная утрата профессиональной трудоспособности на 30% в возрасте 50 лет (мужчины), не выявляемая, но признаваемая и компенсируемая с помощью системы досрочных пенсий по Списку № 1;
8 - постоянная утрата профессиональной трудоспособности на 25% в возрасте 55 лет, не выявляемая, но признаваемая и компенсируемая с помощью системы досрочных пенсий по Списку № 2;
9 – постоянная утрата профессиональной трудоспособности на 20% в возрасте 55 лет, не выявляемая, но признаваемая и компенсируемая с помощью системы досрочных пенсий за выслугу лет (так называемых малых списков – врачи, учителя);
10 – временная утрата трудоспособности по причине профессиональной заболеваемости и производственного травматизма.
Важными и существенными недостатками его организации и функционирования с позиции оценки профессионального риска и обоснованности размеров страховых тарифов выступают следующие институциональные причины.
А). Применяемый в настоящее время финансовый метод при определении классов профессиональных рисков и установления страховых тарифов на этой основе, учитывающий вероятностную природу несчастных случаев и профессиональных заболеваний только косвенным методом на основе фактических затрат, страдает неполнотой (зауженностью) выявляемых страховых случаев, что объясняется историческими причинами.
Поэтому действующая в стране система обязательного социального страхования от несчастных случаев и профессиональных заболеваний все еще не позволяет обеспечивать надежную и необходимую защиту застрахованным работникам.
Б). Применяемый метод «усредненного страхового тарифа» для всей совокупности работников предприятий на основе их отнесения к виду экономической деятельности не может учитывать фактических уровней профессионального риска в его непосредственном социальном и экономическом выражении с позиции повреждения здоровья и утраты трудоспособности. Например, не применяются методы вероятности наступления и тяжесть последствий страховых случаев на протяжении всей жизни застрахованного работника.
В набор инструменталистских методов оценки профессиональных рисков включает также стоимостные методы, которые позволяют определить объем требуемых страховых платежей то есть премий, “степень вины”, а значит и долю платежей для отдельных страхователей, что в конечном итоге позволяет справедливо распределить страховую нагрузку (страховое бремя) между всеми страхователями.
Тем самым, фактически применяемые страховые механизмы оценки последствий профессиональных рисков носят характер усеченного или неполного по масштабу страхового события, что и служит основным препятствием для выявления истинной картины утраты профессиональной трудоспособности в стране.
Это во многом объясняет отсутствие динамики с введением страхования утраты профессиональной трудоспособности, поскольку наиболее сложные и во многом нерешенные вопросы самых ранних форм выявления, профилак-тики компенсации досрочной утраты профессиональной трудоспособности работников, занятых в производствах с вредными и опасными условиями труда, не только не решаются на протяжении последних десятков лет, но даже не ставятся на повестку дня.
Уровень профессионального риска можно охарактеризовать с помощью следующих показателей:
− вероятностью или частотой для данной профессиональной группы работающих за определенный период времени, наступления страховых случаев, приводящих к утрате заработков из-за наступления профессиональных рисков;
− видами (нозологией) и продолжительностью утраты здоровья;
− видами (нозологией) и продолжительностью утраты трудоспособности;
− набором компенсационных выплат, медицинских и реабилитационных услуг, требующихся для конкретной профессиональной группы работающих.
В отличие от утраты общей трудоспособности в связи с нечастным случаем на производстве и профессиональной заболеваемостью, а также старости, где основные страховые характеристики данных пенсионных институтов имеют разработанную нормативную и процедурную базу, утрата профессиональной трудоспособности в связи длительной работой в производствах с вредными условиями труда требует разработки специальных медицинских, социальных и страховых критериев, правовой базы и соответствующих процедур. Кроме того, нельзя не учитывать и неизбежного противодействия со стороны предпринимателей, которые не заинтересованы в дополнительных издержках, неизбежных при введении обязательного социального страхования данных видов профессиональных рисков.
Напомним наиболее существенные для расчета тарифов условия исследуемой страховой схемы. Начиная с момента прихода работника на работу во вредных условиях, охваченную настоящей страховой схемой, от работодателя начинают поступать страховые взносы с целью обеспечения в дальнейшем следующих страховых обязательств. При достижении определенного возраста за пять или за десять лет до выхода на общегосударственную пенсию по старости работнику назначается пенсия или дополнительная пенсия, которая выплачивается вплоть до выхода на пенсию по старости. Если же до момента назначения дополнительной пенсии обнаруживается, что здоровье работника по причине профессиональных рисков вообще не позволяет ему работать на этом производстве, работник переводится на менее вредную и хуже оплачиваемую работу и ему назначается компенсация, которая выплачивается регулярно вплоть до выхода на дополнительную пенсию. В случае внезапной смерти работника или его ухода с вредного производства по причинам, не связанным с предметом страхования, все средства, накопленные на выплату ему компенсаций, исключаются из резерва.
Случайным событием в данной схеме является ухудшение здоровья работника, приводящее к необходимости перевода его на другую работу с менее вредными условиями труда и выплате компенсаций утраченного заработка. Моментом наступления этого события является констатация утери предельно допустимой доли здоровья, что фиксируется медицинскими экспертами при ежегодной диспансеризации.
В качестве единицы времени рассматривается один календарный год. В том случае, когда взносы или выплаты производятся чаще, в формулах им соответствуют суммы за год соответствующиз эквивалентов их значений, вычисленные на конец соответствующего года. Момент наступления страхового события мы также относим на конец соответствующего года и считаем, что взносы за текущий год поступают, а выплаты начнутся уже со следующего года.
Для того чтобы упростить формулы и не загромождать выкладки расчетами номинальных значений разнообразных сумм в разные моменты времени, мы будем выписывать формулы и уравнения в эквивалентах на рассматриваемый момент времени.
Размеры компенсаций устанавливаются как денежные суммы, величина которых зависит от потерь в заработной плате при переходе на рабочее место или производство с менее вредными условиями, поэтому для разных работников эти величины могут принимать разные значения.
При назначении размера пенсий учитывается и доля утерянного в связи с вредными условиями работы здоровья.
Страховые взносы устанавливаются только в зависимости от заработной платы работника и стажа работы во вредных условиях.
Будут использованы следующие обозначения:
− текущий момент времени,
− момент начала участия работника 
в данной пенсионной схеме,
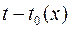− стаж участия работника в данной пенсионной схеме на момент времени ,
− возраст застрахованного работника на момент прихода на вредные условия работы,
− возраст, достижение которого дает право на дополнительную пенсию,
− возраст, достижение которого дает право на пенсию по старости,
− стаж работы в условиях страхового договора к моменту наступления страхового события. Распределение величины сосредоточено на следующем множестве
(146)
оно может быть разным у разных работников, причем 
. (147)
Наступление страхового события в моменты 
приводит к назначению компенсаций, а событие 
обязательно влечет выход на дополнительную пенсию. Если работники 
и 
имеют одинаковый возраст, то и распределения величин 
и 
одинаковы. То есть величины , …, 
для работников 
, находящихся в одинаковых условиях, являются независимыми случайными величинами.
При необходимости обозначения сумм, выплачиваемых в момент , мы будем снабжать нижним индексом . Эквиваленты (на момент ) денежных сумм снабжаем верхним индексом . Так, сумма 
, выплачиваемая в момент времени 
, может быть обозначена как 
, а ее эквивалент на момент , как 
.
Основное условие работы данной страховой схемы состоит в том, что сумма обязательств по отношению к отдельным работникам обеспечивается суммой накопленных взносов на всех работников, охваченных страховым договором. В актуарных расчетах используется известное уравнение баланса, которое приравнивает (на каждый момент времени) математическое ожидание размера страховых резервов к математическому ожиданию суммы принятых обязательств. Выполнение этого уравнения может быть обеспечено выполнением индивидуальных уравнений баланса абсолютно для всех застрахованных работников. В правой части уравнения баланса для отдельного работника стоит математическое ожидание суммы обязательств по отношению к данному работнику то есть эквивалент для этой суммы на момент времени обозначим 
. В левой же части уравнения должно стоять математическое ожидание суммы, которая будет накоплена на условном счету работника к моменту наступления страхового события то есть ее эквивалент на момент времени обозначим 
. Обе суммы в математической модели являются случайными величинами, так как их значения зависят от случайного момента наступления самого страхового события. Индивидуальное уравнение баланса будет иметь вид
