Общий принцип построения границ собственной и падающей тени для поверхности вращения с криволинейной образующей заключается в следующем. Аксонометрический очерк тела перпендикулярно оси вращения разбивается по параллелям на n поясов. Определяя истинный диаметр каждой параллели и используя известные коэффициенты искажения по аксонометрическим и вспомогательным осям, строим относительно соответствующих центров n эллипсов параллелей. По заданным или выбранным направлениям лучей r света и их вторичным проекциям r1 проецируем построенные эллипсы параллелей на опорную поверхность.
Далее вокруг проекций этих эллипсов на опорной поверхности проводим обводочную кривую, которая будет являться границей тени, падающей от тела вращения. Точки касания обводочной кривой с каждым из эллипсов в направлении, противоположном направлению лучей r света, переносим на соответствующие эллипсы параллелей аксонометрического очерка тела. Соединяя полученные точки плавной кривой линией с учётом видимости, получаем границу собственной тени. В дальнейшем необходимо удалить все вспомогательные линии построения и нанести компоненты светотени, получая в результате технический рисунок изображённого тела.
Рассмотрим данную методику на примере построения технического рисунка тела со сферической поверхностью в прямоугольной изометрии. При известном диаметре D сферы из точки O радиусом, равным 1,22 D/ 2, проводим окружность, которая является аксонометрическим очерком сферы, и оси хA , yA и z A (рис. 5.12).
На оси zA отмечаем верхний N и нижний P полюса сферы, так как NP=D. От центра O сферы отрезки ON и OP делим на n равных частей (в нашем случае на три части) и отмечаем точки 
, 1 и 
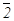, 2 на оси zA.
Если изображаемую сферу через точки 0, , 1 и 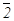, 2 рассечь плоскостями, перпендикулярными оси z, то на её поверхности получим пять окружностей-параллелей. Для построения аксонометрических проекций параллелей необходимо знать их диаметры. Истинные диаметры параллелей можно определить, если через точки деления 
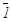, 1 и 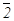, 2 провести горизонтальные прямые до пересечения с окружностью радиуса, равного D/ 2 =ON. Так, например, диаметр параллели с центром в точке 1 будет равен отрезку 3-4.
Через точки , 1 и 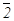, 2 проводим аксонометрические оси, параллельные xA и yA , и строим каждую параллель в прямоугольной изометрии. При построении изометрии параллели, проходящей через точку O, на вспомогательных горизонтальной и вертикальной осях в обе стороны от точки O откладываем отрезки, равные соответственно 1,22 D/ 2и 0,7 D/ 2, а по осям xA и yA – D/ 2.
Соединяя полученные точки плавной кривой, получаем изображение экватора сферы в изометрии. аналогично получаем изометрические проекции других параллелей, помня, что каждая из них имеет свой диаметр.
Пусть сфера своим нижним полюсом P стоит на плоской опоре. На пересечении лучей света, проведённых из точек 0, 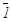, , 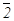1 и 2, и их вторичных проекций, проведённых из точки P, находим точки 00, 
, 
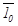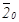, 10 и 20 , которые являются центрами теней от соответствующих изометрических проекций параллелей сферы.
Так как изометрические проекции параллелей и тени от них находятся в параллельных плоскостях, то эллипсы на плоской опоре изображаются без искажений.
Для осуществления параллельного переноса через точки 00, 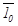, , 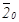10 и 20 проводим вспомогательные горизонтальные и вертикальные оси, а также оси, параллельные хA и yA, на которых откладываем соответствующие отображаемому эллипсу отрезки. Вокруг полученных эллипсов с центрами в точках 00, 
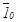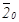, , 10 и 20 проводим обводочную кривую a0 , которая всегда будет эллипсом, кроме случая направления лучей света r параллельно оси z, и является границей падающей от сферы тени.
Отмечаем точки касания обводочной кривой с каждым из эллипсов и проводим параллельно направлению лучей света r линии до пересечения с соответствующими изометрическим проекциями параллелей сферы. Последовательно соединяя полученные точки с учётом видимости, получаем границу a собственной тени на сфере.
Технический рисунок шара при заданном направлении лучей света и его вторичных проекций r1 можно считать завершённым лишь после нахождения границ собственной и падающей теней, аннулирования вспомогательных и дополнительных линий построения и нанесения компонентов светотени на сферической и опорной поверхностях (рис. 5.13).
