Частини, суграфи і підграфи графу.

Операції з частинами графу

Визначення. Граф Н називається частиною графу G (позначається H Í G), якщо:

а) V (H) Í V (G);

б) E (H) Í E (G).

Визначення. Граф Н називається суграфом графу G, якщо він є частиною графу G і

V (H) = V (G).

На Рис. 4 зображені граф G і його три частини. Граф H 3 є суграфом.

 

Рис.4.

 

Визначення. Суграф H називається покриваючим для графу G, якщо будь-яка вершина H інцидентна хоча б одному ребру з G. Зауважимо, що якщо в графі G є ізольовані вершини, то для нього не існує покриваючого графу H.

Визначення. Підграфом G (U) графу G (V) називається така його частина, яка містить всі ребра графу G (V), що з’єднують дві будь-які вершини з множини U.

На рис. 4 H 1 не є підграфом G (не містить ребро e (2, 4)), а H 2 – підграф графу G.

Визначення. Зірковим графом, який визначається деякою вершиною a Î V, називається граф, що містить всі ребра даного графу G (V), інцидентні вершині „ a ”.

За аналогією з операціями поміж множинами можна виконувати і операції між графами.

Визначення. Якщо H – частина графу, то 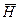(доповнення графу H) – це граф, в який входять всі ребра графу G, які не належать H:

.

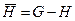Визначення. Нехай H ₁ і H ₂ - дві частини графу G. Тоді H = H ₁ È H ₂ (об’єднання або сума) це також частина графу G, яка складається зі всіх ребер, що належать або H ₁ або H ₂.

Визначення. Нехай H ₁ і H ₂ - дві частини графу G. Тоді H = H ₁ Ç H ₂ (перетин) це частина графу G, яка складається зі всіх ребер, що належать H ₁ та H ₂ одночасно.

Визначення. Якщо дві частини H ₁ і H ₂ графу G не мають спільних вершин, то їх сума H = H ₁ È H ₂ називається прямою. Якщо H ₁ і H ₂ не перетинаються по ребрах, то їх сума називається прямою по ребрах.

Наприклад: - пряма сума за ребрами.

 

Маршрути, ланцюги і цикли

Деякі визначення

 

Нехай G - неорієнтований граф.

Визначення. Маршрутом в G називається скінченна або нескінченна послідовність ребер S = {…, e ₀, e ₁, …, e_n, …} в якій кожні два сусідні ребра e_{i - 1} і e_i мають спільну вершину, тобто

e ₀ = (v ₀, v ₁)

e ₁ = (v ₁, v ₂)

e ₂ = (v ₂, v ₃)

...

e_n = (v_n, v_{n + 1}).

 

Визначення. Якщо в S немає ребер, які стоять перед e ₀, то v ₀ називається початковою вершиною S; якщо немає ребер після e_{n - 1}, то v_n - кінцевою вершиною. Якщо вершина v_i належить і e_{i - 1} і e_i, то вона називається внутрішньою.

Визначення. Якщо маршрут S має початкову і кінцеву вершини, то він називається скінченним; якщо S має початок і не має кінцевої вершини (або навпаки), то він називається односторонньо-нескінченним; якщо немає ні початкової вершини ні кінцевої – то двосторонньо-нескінченними. Якщо S має початкову вершину v ₀ і кінцеву v_n, то позначається

S = S (v ₀, v_n)

(тобто S - це маршрут довжини n, який з’єднує вершини v ₀ і v_n).

Визначення. Якщо v ₀ = v_n, то маршрут називається циклічним.

Визначення. Якщо v_i і v_j - дві вершини маршруту S, то

S (v_i, v_j) = (e_i, …, e_{i + 1}, …, e_{j - 1})

називається підмаршрутом.

На рис.5 маршрут S = (e ₁, e ₂, e ₃, e ₄, e ₅) є скінченним, має довжину 5, початкову вершину v ₁ і кінцеву v ₅. Маршрут S = (e ₂, e ₃, e ₄) є підмаршрутом даного маршруту.

 

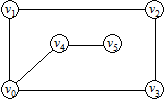
Рис.5

 

Визначення. Ланцюг – це маршрут, кожне ребро якого зустрічається рівно один раз. Циклічний ланцюг називається циклом.

Визначення. Нециклічний ланцюг називається простим, якщо в ньому жодна вершина не повторюється. Цикл з початком (і кінцем) в v ₀ називається простим, якщо в ньому жодна вершина, крім v ₀ не повторюється.

Зрозуміло, що частина ланцюга або циклу теж є ланцюгом або циклом.

Для орієнтованих графів вводяться в розгляд як неорієнтовані маршрути (ланцюги) (тобто не приймається до уваги орієнтація ребер), так і орієнтовані маршрути (ланцюги).

 

Зв’язаність

 

Нехай G - неорієнтований граф.

Визначення. Дві вершини „ a ” і „ b ” графу G називаються зв’язними, якщо існує маршрут S (a, b).

Якщо в S (a, b) деяка вершина v_i повторюється більше одного разу, то відкидаючи циклічну ділянку S (v_i, v_i), отримаємо новий маршрут S ’(a, b), в якому вершина v_i зустрічається тільки один раз. Повторюючи цю процедуру для всіх таких вершин v_i, приходимо до висновку: якщо дві вершини в графі можуть бути зв’язані маршрутом, то існує і простий ланцюг, який зв’язує ті ж вершини.

Визначення. Граф G називається зв’язним, якщо зв’язна будь-яка його пара вершин.

Всі підграфи G (V_i) зв’язного графу G (V) є теж зв’язними і називаються зв’язними компонентами графу.

Зауважимо, що зв’язність – відношення еквівалентності між вершинами графу:

а) довільна вершина v графу зв’язана сама з собою;

б) якщо „ a ” і „ b ” – зв’язні (тобто існує маршрут S (a, b)), то в силу неорієнтованості графу „ b ” і „ а ” теж зв’язані (маршрутом S (b, a));

в) якщо зв’язані „ а ” і „ b ” (маршрутом S ₁(a, b)) і „ b ” і „ с ” (маршрутом S ₂(b, c)), то існує маршрут з „ а ” в „ с ” (S ₁(a, b) + S ₂(b, c)), тобто вершини „ a ” і „ c ” теж зв’язані.

В силу відомого твердження з алгебри, граф G розбивається на класи еквівалентності – підграфи, в яких всі вершини є зв’язаними між собою і які не мають спільних вершин:

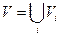, (пряма сума)

таким чином, істинне

Твердження. Довільний неорієнтований граф розбивається на пряму суму своїх зв’язаних компонент.

Це дозволяє більшість задач зводити до випадку зв’язаних графів.