Відображення f множини Х в множину Y називають ін’єктивним, чи ін’єкцією, якщо двом різним елементам з множини Х відповідають два різних елементи з множини Y (рис. 9а та 9в). Іншими словами f : X → Y ін’єктивне, якщо для будь-яких x ≠ x 1, x, x 1 Î Х, f (x) ≠ f (x 1).
Зауважимо, зокрема, що канонічна ін’єкція деякої підмножини в саму множину є ін’єктивним відображенням.
Відображення f називають сюр’єктивним, чи сюр’єкцією, якщо для кожного елемента y з множини Y існує принаймні один елемент x з множини X такий, що f (x)= y. (рис. 9б та 9в).
Відображення називають бієктивним, чи бієкцією, якщо воно одночасно ін’єктивнe та сюр’єктивнe. Відображення f є бієктивним, якщо кожен елемент із Y є образом при відображенні f деякого, і при тому єдиного, елемента з X (рис. 9в). Кажуть, що бієктивне відображення встановлює взаємно однозначну відповідність між множинами X та Y. Бієкція множини на себе називається також перестановкою чи перетворенням.
Рис. 9
Для скінченних множин Х та Y сюр’єктивнiсть відображення f : X → Y означає, що | Х | ≥ | Y |. Наприклад; f : {1, 2, 3, 4} → { y 1, y 2, y 3}, f = 
- сюр’єктивне, a f = 
- не сюр’єктивнe.
Якщо Х і Y скінченні, то ін’єктивність відображення означає, що | Х | ≤ | Y |.
Наприклад, нехай Х = {l, 2, 3}, Y = { y 1, y 2, y 3, y 4}. Якщо f (1) = y 1, f (2) = y 2, f (3) = y 3, то f : X → Y ін’єктивнe.
При скінченних X та Y бієктивнiсть відображення f : X → Y означає, що | X | = | Y |.
Наприклад, X = (1, 2, 3), Y = { y 1, y 2, y 3}, відображення f = 
- бієктивне.
Композиція відображень
Нехай задано два відображення: f : X → Y та g: Y → Z. Тоді композицією відображень f і g (позначаємо символом g ○ f) будемо називати відображення з множини X в множину Z, визначене виразом g ○ f (x) = g (f (x)) для всіх елементів x з множини X. Прийняте правило, згідно з яким у композиції g ○ f треба починати з відображення f, розташованого праворуч.
Наприклад, нехай маємо множини Х = {l, 2, 3, 4}, Y = { а, b, c }, Z = { u, v }та два відображення
f : Х → Y, 
, g : Y → Z, 
Тоді композиція заданих відображень g ○ f: Х → Z, 
Композиція відображень асоціативна, тобто якщо маємо три відображення f : X → Y, g: Y → Z, h: Z → U, то (h ○ g) ○ f = h ○ (g ○ f) = h ○ g ○ f.
Відображення g: Y → X називається оберненим до відображення f : X → Y, якщо виконуються такі умови f -1 ○ f = IX (IX - тотожне відображення на множині X), f ○ f -1 = IY (IY - тотожне відображення на множині Y).
Для відображення f існує обернене відображення f -1 тоді і тільки тоді, коли відображення f бієктивне. Обернене відображення f -1 також є бієктивним.
Якщо f : X → Y - бієкція й g: Y → Z - бієкція, то g ○ f - бієкція з Х в Z, а її обернена бієкція дорівнює f -1 ○ g -1.
Наприклад, нехай задані множини Х ={l, 2, 3}, Y = { а, b, c } та відображення f : Х → Y, 
. Це відображення є бієктивним, і тому до нього існує обернене f -1: Y → X,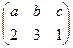 
. Дійсно, f -1 ○ f = 
= IX та f ○ f -1 = 
= IY.
Відношення
Розглянемо декартовий добуток другого степеня множини Х: Х2 = Х ´ Х. Довільну підмножину R множини Х2 (R Í Х2) будемо називати бінарним відношенням (або просто відношенням), заданим на множині Х. Вважатимемо, що впорядковані елементи x, х' Î Х знаходяться між собою у відношенні R, коли (x, х') Î R. Якщо на Х задано відношення R Í X 2, то запис x R х' означає, що x і х' знаходяться у відношенні R, тобто(x, х') Î R.
Розглянемо кілька прикладів відношень:
1) на множині N відношення £. Ясно, що впорядковані пари (3, 7) і (5, 5) належать цьому відношенню, а пара (4, 1) не належить;
2) на множині Р (Х) всіх підмножин множини Х = {1, 3, 5, 7, 9} відношення Í. Пари підмножин ({1, 3}, {1, 3, 9}) і ({5, 7, 9}, {5, 7, 9}) належать цьому відношенню, а пара підмножин ({1, 5, 7}, {3, 5, 9}) не належить.
Відношення R на множині X називається:
1) рефлективним, якщо довільний елемент множини знаходиться у відношенні сам з собою, тобто для будь-якого х Î Х виконується х R х. Прикладами рефлективних відношень можуть бути ≤, ≥, = на множині натуральних чисел;
2) антирефлективним, якщо для будь-якого х Î Х пара (х, х) не належить до відношення R. Прикладами антирефлективних відношень можуть бути <, >, ≠ на множині раціональних чисел;
3) симетричним, якщо для довільних x, х' Î Х з того, що x R х' випливає х' R x;
4) антисиметричним, якщо для довільних x, х' Î Х з того, що x R х' і х' R x, випливає x = х' (наприклад, £ на N, тому що з x £ х' і х' £ x випливає х = х');
5) транзитивним, якщо для довільних x, х', х'' Î Х з того, що x R х' і х' R х'', випливає x R х'' (наприклад, відношення Í на множині Р (Х) чи відношення £ на множині N).
Наведемо деякі приклади відношень:
1) R = {(x, х ') | x, х ' Î Q, | x - х ' | £ 2007}
Відношення рефлективне, бо для будь-якого x Î Q виконується нерівність | x - х | £ 2007
Відношення не є антирефлективним, бо скажімо для елемента x =5Î Q нерівність | x - х | £ 2007 виконується.
Відношення є симетричним, бо для довільних x, х ' Î Q, з нерівності | x - х ' | £ 2007 випливає нерівність | x ' - х | £ 2007
Відношення не є антисиметричним, бо для різних елементів x =7 та x '=5 з множини Q одночасно виконуються нерівності | x - х ' | £ 2007 та | x ' - х | £ 2007
Відношення не є транзитивним, бо для елементів x =2010, x '=1 та x ''=10 з множини Q нерівності | x - х ' | £ 2007 та | x ' - x '' | £ 2007 виконуються, а нерівність | x - х '' | £ 2007 не виконується.
2) R = {(x, y) | x, y Î С, якщо | x | £ | y | £ | y 2|}
Розглянемо далі відношення, які мають особливе значення.
