1. Алгебра складається з усіх відображень множини {1,2} в себе: 
, 
, 
, 
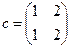. Операцією є композиція ○ відображень. Скласти таблицю Келі та дослідити властивості операції в цій алгебрі.
Розв‘язування. Таблиця Келі для операції ○ в заданій алгебрі має вигляд
| ○ | а | b | c | d |
| а | a | b | a | b |
| b | a | b | b | a |
| c | a | b | c | d |
| d | a | b | d | c |
Як відомо композиція відображень є асоціативною, отже алгебра A = (X; ○} є півгрупою, де X = { a, b, c, d }. У півгрупі A є одиничний (нейтральний) елемент c, оскільки " x Î X, x ○ c = c ○ x = x. Отже, півгрупа A є моноїдом. Оскільки a ○ b = b, а b ○ a = a, то моноїд не є абелевим.
2. Перевірити, чи утворює групу множина R + операція T, якщо вона задається як a T b = a 2 b 4.
Розв‘язування. Для того, щоб алгебра була групою необхідно, щоб у алгебрі існував нейтральний елемент. Умовою існування нейтрального елемента e є " x Î R +, e T x = x T e = x. Нехай e 1 –лівий, а e 2 –правий нейтральний елементи. Тоді e 1 T x = e 12 x 4 = x, звідси e 1 = x –3/2. Разом з тим x T e 2 = x 2 e 24 = x і e 2 = x –1/4. Як бачимо e 2 ≠ e 1. Таким чином, нейтрального елемента не існує, і тому задана алгебра не є групою.
3. Показати, що група додатних дійсних чисел відносно операції множення (R +; ×) ізоморфна групі дійсних чисел відносно операції додавання (R; +).
Розв‘язування. Для доведення ізоморфізму можна використати наступне бієктивне відображення ln: R + ® R, яке зберігає групові операції - ln (a × b) = ln (a) + ln (b).
4. Довести, що множина всіх чисел виду 
(a та b – цілі числа), які додаються та множаться як звичайні дійсні числа, є кільцем.
Розв‘язування. Справді, замкнутість цієї множини відносно операцій додавання та множення випливає зі співвідношень () + (
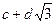) = (a + b) + (c + d) 
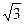та ()()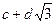 = (ac + 3 bd) + (ad + bc) 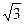. Таким чином, наведені операції є дійсно бінарними операціями на заданій множині.
Перевіримо спочатку, що задана множина з операцією додавання є абелевою групою. Оскільки числа виду є частковим випадком дійсних чисел, то операція їх додавання є асоціативною й комутативною. Нейтральним елементом відносно додавання, очевидно, є елемент 
. Оберненим для елемента відносно операції додавання є елемент 
.
Числа виду є частковим випадком дійсних чисел. Тому й операція їх множення є асоціативною. Значить, вказана множина відносно заданої операції множення є півгрупою.
Як згадувалося раніше, операції множення та додавання на заданій множині є операціями над дійсними числами. Тому вказана операція множення є дистрибутивною відносно операції додавання.
Отже множина всіх чисел виду (a та b – цілі числа), які додаються та множаться як звичайні дійсні числа, є кільцем.
Зауважимо, що згадана множина не є полем, бо не існує нейтрального елемента відносно операції множення, як показують наступні міркування.
Нехай 
- нейтральний елемент відносно операції множення. Тоді повинна виконуватися рівність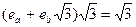 
. З неї отримуємо, що 
. Як бачимо зліва стоїть ціле число, а справа – ірраціональне. Ми отримали суперечність.
Елементи теорії графів
Вступ
Теорія графів, як розділ дискретної математики, з успіхом використовується у задачах керування виробництвом і проектування мереж ЕОМ, при розробці сучасних електронних модулів і при проектуванні фізичних систем, при розробці сучасних електронних модулів і при проектуванні фізичних систем, при розв’язуванні задач генетики і вирішенні проблем автоматизованого управління (САПР). Теорія графів є основою математичного забезпечення сучасних систем обробки інформації у прикладній теорії алгоритмів та в інших галузях науки і техніки.
Далі будемо розглядати деякі елементи теорії графів, які мають загальну форму та можуть бути застосовані при дослідженні об’єктів та систем довільної природи.
