Поняття множини. Способи задання множин

Міністерство Освіти і Науки України

Національний Університет “Львівська Політехніка”

Кафедра ЕОМ

Навчальний посібник

з курсу “Дискретна математика”
для студентів базового напрямку 6.0915 “Комп’ютерна інженерія”

Затверджено
на засіданні кафедри
Електронних Обчислювальних Машин
Протокол № від 24 квітня 2007 року

Львів – 2007

Навчальний посібник з курсу “Дискретна математика” для студентів базового напрямку 6.0915 “Комп’ютерна інженерія” / Укладач: Р. Попович – Львів: Національний університет “Львівська політехніка”, 2007, с.

Укладач: Р. Попович, к.т.н., доцент

Відповідальний за випуск: Мельник А. О., професор, завідувач кафедри ЕОМ

Рецензенти:

Елементи теорії множин

Вступ

Дискретна математика є розділом математики, що зародилася в давні часи. Її головною відмінністю є дискретність, тобто антипод неперервності. Дискретна математика включає традиційні розділи математики, які вже сформувалися (математичну логіку, алгебру, теорію чисел), і нові, що інтенсивно розвиваються.

У більш як двотисячорічній історії дискретної математики сучасний період є одним із найінтенсивніших періодів її розвитку: дуже швидко розширюється сфера застосування, інтенсивно зростають обсяги нової інформації та кількість нових результатів. Якщо ще порівняно недавно ця наука була сферою інтересів лише вузького кола фахівців, то тепер вона перетворюється на наукову дисципліну, дуже важливу й потрібну для багатьох, а у сфері сучасної освіти – для всіх.

Масове використання обчислювальної техніки та інформаційних технологій значно розширює сферу прикладних досліджень, у яких все більше застосовується апарат дискретної математики.

Базовим розділом як дискретної математики, так і взагалі всієї математики, є теорія множин.

Коротка історична довідка

Основи теорії множин були закладені відомим німецьким математиком Георгом Кантором у другій половині минулого століття. Поява теорії множин була зустрінута з ентузіазмом багатьма авторитетними математиками. Вони побачили в ній можливість створення метамови математики, тобто формальної одностайної системи понять і принципів, за допомогою якої можна було б викласти з єдиних позицій зміст різноманітних традиційно далеких один від одного розділів математики. Перші такі досить успішні спроби були виконані вже незабаром після виникнення канторівської теорії множин.

Однак пізніші дослідники виявили в теорії Кантора чимало суперечностей: так званих парадоксівабо антиномій теорії множин. Виникла кризова ситуація. Одна частина математиків, посилаючись на штучність сформульованих антиномій, вважала за краще не помічати ці суперечності або не надавати їм великого значення. У той час як інша (скажімо, відповідальніша) група математиків зосередила свої зусилля на пошуках більш обгрунтованих та точних принципів і концепцій, на яких могла б бути побудована несуперечлива теорія множин.

У результаті було запропоновано кілька формальних (або аксіоматичних) систем, які служать фундаментом сучасної теорії множин, а значить, фундаментом всієї класичної математики. Важливість цих досліджень серед іншого підкреслює той факт, що значний внесок у становлення аксіоматичної теорії множин зробили такі видатні математики і мислителі XX століття, як Б.Рассел, Д.Гільберт, К.Гедель та ін.

Сьогодні теорія множин - це математична теорія, на якій грунтується більшість розділів сучасної математики, як неперервної, так і дискретної.

Поняття множини. Способи задання множин

Для наших цілей достатньо буде викладення основ так званої інтуїтивноїабо наївної теорії множин, яка в головних своїх положеннях зберігає ідеї та результати засновника теорії Г.Кантора.

В інтуїтивній теорії множин поняття "множина" належить до первинних невизначальних понять, тобто воно не може бути означено через інші більш прості терміни або об’єкти, а пояснюється на прикладах, апелюючи до нашої уяви та інтуіції. Такими поняттями в математиці є також поняття "число", "пряма", "точка", "площина" тощо.

Канторівський вираз: "Множина - це зібрання в єдине ціле визначених об’єктів, які чітко розрізняються нашою інтуіцією або нашою думкою" - безумовно не може вважатися строгим математичним означенням, а є скоріше поясненням поняття множини, яке заміняє термін "множина" на термін "зібрання". Іншими синонімами основного слова "множина" є "сукупність", "набір", "колекція", "об’єднання" тощо.

Прикладами множин можуть служити: множина десяткових цифр, множина літер українського алфавіту, множина мешканців Львова, множина парних чисел, множина розв’язків деякого рівняння та ін.

На письмі множини позначаються, як правило, великими літерами. Для деяких множин у математиці вживаються сталі позначення. Наприклад, N - множина натуральних чисел, Z - множина цілих чисел, Q - множина раціональних чисел, R - множина дійсних чисел, C - множина комплексних чисел тощо.

Об’єкти, з яких складається задана множина, називають її елементами. Елементи множин позначатимемо малими літерами латинського алфавіту. Той факт, що об’єкт a є елементом множини M записується так: a Î M (читається: " a належить M " або" a є елемент M "). Для того, щоб підкреслити, що деякий елемент a не належить множині M, вживають позначення a Ï M.

Запис a, b, c,...Î M використовують для скорочення запису a Î M, b Î M, c Î M,....

Множину називають скінченною, якщо кількість її елементів скінченна, тобто існує натуральне число k, що є числом елементів цієї множини. В іншому разі множина є нескінченною.

Множина є визначеною, коли можна встановити, чи є будь-який об’єкт її членом чи ні.

Для задання множини, утвореної з будь-яких елементів, будемо використовувати два такі способи. В основі обох із них лежить позначення множини за допомогою фігурних дужок.

1. Якщо a ₁, a ₂,..., a_n - деякі об’єкти, то множина цих об’єктів позначається через { a ₁, a ₂,..., a_n }, де у фігурних дужках міститься перелік усіх елементів відповідної множини. З останнього зауваження випливає, що в такий спосіб можуть бути задані тільки скінченні множини. Порядок запису елементів множини при цьому позначенні є неістотним.

Так, множина десяткових цифр записується {0,1,2,3,4,5,6,7,8,9}, множина основних арифметичних операцій - {+,-,*,/} або {*,/,+,-}, множина розв’язків нерівності (x -1)² £ 0 - {1}.

Слід пікреслити, що однією з основних ідей канторівської теорії множин був розгляд множини як нового самостійного об’єкта математичного дослідження. Тому необхідно розрізняти такі два різні об’єкти, як елемент a і множина { a }, яка складається з єдиного елемента a. Зокрема, множини можуть виступати в ролі елементів якоїсь іншої множини. Наприклад, множина всіх можливих невпорядкованих пар з елементів a, b і c (елементи в парі не співпадають) D = {{ a, b },{ a, c },{ b, c }} складається з трьох елементів і задана цілком коректно.

2. Другий спосіб задання множин грунтується на зазначенні загальної властивості або породжувальної процедури для всіх об’єктів, що утворюють описувану множину.

У загальному випадку задання множини M має вигляд: M = { a | F (a)}.

Цей вираз читається так: "множина M - це множина всіх таких елементів a, для яких виконується властивість F ", де через F (a) позначено властивість, яку мають елементи множини M і тільки вони.

S = { n | n - непарне число } або S = { n | n = 2 k +1, k Î Z },

X = { x | x = p k, k Î Z },

F = { f_i | f_i ₊₂ = f_i ₊₁ + f_i, i Î N, f ₁ = f ₂ = 1 }.

Другий спосіб є більш загальним способом задання множин. Наприклад, введену вище множину D всіх невпорядкованих пар з елементів a, b і c можна задати так

D = { { x, y } | x Î{ a, b, c }, y Î{ a, b, c } і x ¹ y }.

Надалі будемо використовувати такі загальноприйняті позначення для числових множин, з якими часто зустрічаємось:

N ={1,2,3,…} – множина натуральних чисел;

Z ={…,-2,-1,0,1,2,…} – множина цілих чисел;

Q – множина раціональних чисел;

R – множина дійсних чисел;

C – множина комплексних чисел.

Множину називаємо скінченною, якщо вона має скінченне число елементів, і нескінченною, якщо вона має нескінченне число елементів.

У теорії множин використовується поняття порожньої множини. Вона позначається символом Æ.

Множина може взагалі не містити елементів, наприклад

S = { x | x – непарне число, що ділиться на 2} = Æ;

K = { x | x Î R, x ² + 1 = 0} = Æ.

Для позначення цього факту вводиться поняття порожньої множини.

Це поняття відіграє дуже важливу роль при заданні множин за допомогою опису. Так, без поняття порожньої множини не можна говорити про множину відмінників студентської групи або про множину дійсних коренів квадратного рівняння, не пересвідчившись заздалегідь, чи є в студентській групі відмінники або чи має задане рівняння дійсні корені. Поняття порожньої множини дає змогу оперувати множиною відмінників групи, не турбуючись про те, чи є відмінники в групі, яка розглядається. Порожню множину умовно відносять до скінченних множин. Число елементів у ній рівне 0.

Таким чином, уведення порожньої множини дає можливість оперувати будь-якою множиною без попереднього застереження, існує вона чи ні.

Операції над множинами

Розглянемо дві множини А і В та введемо низку операцій над ними. Для графічної ілюстрації використовують діаграми (кола) Ейлера. Для зображення множини на площині креслять замкнену лінію із заштрихованою внутрішньою областю (найчастіше – це коло, звідси й назва відповідного інструмента, що широко застосовується в теорії множин).

Об’єднання А і В – множина, що складається з усіх елементів множини А, всіх елементів множини В і не містить ніяких інших елементів (рис. 1), тобто

А È В = { x | x Î А або x Î В }.

Рис. 1

Перетин А і В – множина, що складається з тих і тільки з тих елементів, які належать одночасно множині А та множині В (рис. 2), тобто

А Ç В = { x | x Î А і x Î В }.

Рис. 2

Різниця А і В (відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині А й не належать множині В (рис. 3), тобто

А \ В = { x | x Î А і x Ï В }.

Рис. 3

Диз’юнктивна сума А і В (симетрична різниця) – множина, що складається усіх елементів А, які не належать множині В, й усіх елементів В, які не належать множині А, та яка не містить ніяких інших елементів (рис. 4), тобто

А Å В = { x | (x Î А і x Ï В) або (x Î В і x Ï А)}.

Рис. 4

Доповнення множини.

Звичайно, вже в означенні конкретної множини явно або неявно обмежується сукупність об’єктів, що є допустимими (слони – серед тварин, натуральні числа – серед цілих або дійсних залежно від контексту). Зручно сукупність допустимих об’єктів зафіксувати явно та вважати, що множини, які розглядаються, складаються з елементів цієї сукупності. Її називають основною множиною (універсумом) і позначають U. Універсум U арифметики – числа, універсум U зоології – тварини і т.д. Будь-яку множину розглядатимемо у зв’язку з універсумом, який на діаграмах Ейлера асоціюватимемо з прямокутником на площині, всередині якого зображатимемо множини (рис. 5).

Рис. 5

Доповнення множини А – це множина, що містить усі елементи універсуму, за винятком елементів А (рис. 6), тобто .

Рис.6

Множина А називається підмножиною множини В, якщо кожен елемент А є елементом В. Для позначення цього факту вводиться знак Ì - символ строгого включення (або Í - символ нестрогого включення) (рис. 7). Якщо необхідно підкреслити, що множина В містить також інші елементи, крім елементів множини А, то використовують символ строгого включення А Ì В.

Дві множини рівні, якщо вони складаються з одних і тих самих елементів. Справджується таке: А = В тоді і тільки тоді, коли А Í В і В Í А.

Рис. 7

Окремо розглянемо ще одну дуже важливу операцію над множинами.

Декартовим (прямим) добутком множин A і B (записується A ´ B) називається множина всіх пар (a, b), в яких перша компонента належить множині A (a Î A), а друга - множині B (b Î B).

Тобто

A ´ B = {(a, b) | a Î A і b Î B }

Декартовий добуток природно узагальнюється на випадок довільної скінченної сукупності множин. Якщо A ₁, A ₂,..., A_n - множини, то їхнім декартовим добутком називається множина

D = { (a ₁, a ₂,..., a_n) | a ₁Î A ₁, a ₂Î A ₂,..., a_n Î A_n },

яка складається з усіх наборів (a ₁, a ₂,..., a_n), в кожному з яких i -й член, що називається i -ю координатою або i -ю компонентою набору, належить множині A_i, i =1,2,..., n. Декартовий добуток позначається через A ₁´ A ₂´...´ A_n.

Набір (a ₁, a ₂,..., a_n), щоб відрізнити його від множини, яка складається з елементів a ₁, a ₂,..., a_n, записують не у фігурних, а в круглих дужках і називають кортежем, вектором або впорядкованим набором. Довжиною кортежу називають кількість його координат. Два кортежі (a ₁, a ₂,..., a_n) і (b ₁, b ₂,..., b_n) однакової довжини вважаються рівнимитоді і тільки тоді, коли рівні їхні відповідні координати, тобто a_i = b_i, i =1,2,..., n. Отже, набори (a, b, c) і (a, c, b) вважаються різними, в той час як множини { a, b, c } і { a, c, b } - рівні між собою.

Декартовий добуток множини A на себе n разів, тобто множину A ´ A ´...´ A називають n -м декартовим (або прямим) степенем множини A і позначають Aⁿ.

Прийнято вважати, що A ⁰ = Æ (n =0) і A ¹ = A (n =1).

Наприклад, якщо A = { a, b } і B = { b, c, d }, то

A ´ B = {(a, b),(a, c),(a, d),(b, b),(b, c),(b, d)},

A ² = {(a, a),(a, b),(b, a),(b, b)}.

Якщо R - множина дійсних чисел або множина точок координатної прямої, то R ² - це множина пар (a, b), де a, b Î R, або множина точок координатної площини.

Координатне зображення точок площини вперше було запропоновано французьким математиком і філософом Рене Декартом, тому введена операція над множинами і називається декартовим добутком.

Множину, елементами якої є всі підмножини множини А, називають множиною підмножин множини А (або булеаном множини А) і позначають Р (А). Так, для триелементної множини А = { a, b, c } маємо P (A)={Æ, { a }, { b }, { c }, { a, b },{ b, c }, { a, c }, { a, b, c }}. У разі скінченної множини А з n елементів, множина підмножин Р (А) містить 2 ⁿ елементів.

Алгебра множин

Операції над множинами, як і операції над числами, мають деякі властивості (табл.). Останні виражаються сукупністю тотожностей незалежно від конкретних множин, що входять у ці тотожності та є підмножинами деякого універсуму U.

Таблиця

Комутативність
1а) А È В = В È А	1б) А Ç В = В Ç А
Асоціативність
2а) А È (В È С) = (А È В) È С	2б) А Ç (В Ç С) = (А Ç В) Ç С
Дистрибутивність
3а) А È (В Ç С) = (А È В) Ç (А È С)	3б) А Ç (В È С) = (А Ç В) È (А Ç С)
Властивості порожньої множини Æ та універсуму U
4а) А È Æ = A	4б) А Ç U = A
5а)	5б)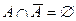
6а) А È U = U	6б) А Ç Æ = Æ
7а)	7б)
Самопоглинання
8а) А È A = A	8б) А Ç A = A
Поглинання
9а) А È (А Ç В) = А	9б) А Ç (А È В) = А
Правило де Моргана
10а)	10б)
Властивості доповнення, різниці, диз’юнктивної суми
11)
12)
13)
14) А Å В = В Å А
15) А Å (В Å С) = (А Å В) Å С
16) А Å Æ = Æ Å A = A

Основний метод доведення тотожностей в алгебрі множин ґрунтується на згаданому раніше факті: А = В тоді і тільки тоді, коли А Í В і В Í А. Доведемо, наприклад, тотожність 3а) А È (В Ç С) = (А È В) Ç (А È С).

Доведемо спочатку, що А È (В Ç С) Ì (А È В) Ç (А È С). Для цього візьмемо будь-яке x Î А È (В Ç С), тоді за означенням операцій È та Ç маємо x Î А або (x Î В і x Î С). За законом дистрибутивності “або” відносно “і” (x Î А або x Î В) і (x Î А або x Î С), тобто x Î А È В і x Î А È С. Це рівносильно x Î (А È В) Ç (А È С), що й треба було довести.

Доведемо тепер, що (А È В) Ç (А È С) Ì А È (В Ç С). Для цього візьмемо будь-яке x Î (А È В) Ç (А È С). Звідси (x Î А або x Î В) і (x Î А або x Î С). Це рівносильно x Î А або (x Î В і x Î С), тобто x Î А È (В Ç С), що й потрібно було довести.

Таким чином, А È (В Ç С) = (А È В) Ç (А È С).

Із властивості асоціативності операції об’єднання множин випливає, що об’єднання кількох множин можна виконати, послідовно об’єднуючи їх, причому порядок входження множин не впливає на результат: А È (В È С) = (А È В) È С = А È В È С. Отже, об’єднання сукупності множин можна подати співвідношенням: .

Аналогічно на n множин узагальнюється операція перетину: .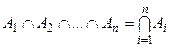

Використовуючи узагальнення операцій об’єднання та перерізу на n множин, можна узагальнити також інші співвідношення, наприклад закон де Моргана, який в узагальненому вигляді записується так: і .

Зауважимо, що операція декартового добутку неасоціативна і некомутативна, тобто множини (A ´ B)´ C і A ´(B ´ C), а також множини A ´ B і B ´ A, взагалі кажучи, не рівні між собою.

Зв’язок декартового добутку з іншими операціями над множинами встановлюється такими тотожностями:

(A È B) ´ C = (A ´ C) È (B ´ C),

(A Ç B) ´ C = (A ´ C)Ç(B ´ C),

A ´ (B È C) =(A ´ B) È (A ´ C),

A ´ (B Ç C) =(A ´ B)Ç(A ´ C).

Сукупність підмножин A ₁, A ₂, …, A_n множини A називається розбиттям множини A, якщо:

1. ;

2. A_i Ç A_j = Æ, i, j =1,.., n, i ¹ j.

Парадокси теорії множин

Слово "парадокс" грецького походження і перекладається українською мовою - несподіваний, дивний. Вживають це слово у відношенні до висловлювання (положення, ідеї), яке суттєво різниться від загальноприйнятого традиційного уявлення з даного приводу. Вживання терміна "парадокс" стосовно до тих суперечностей, які були виявлені різними математиками в теорії множин Г.Кантора, є наївною спробою зменшити їхнє значення і надати їм характеру логічних курйозів, штучних, неприродних конструкцій. Більш точно суть явища передає назва, "антиномії теорії множин", оскільки термін антиномія є синонімом терміна суперечність. Але за традицією, будемо називати сформульовані нижче положення парадоксами.

Парадокс Б.Рассела. Для будь-якої множини M коректним є питання: чи множина M належить собі як окремий елемент, тобто чи є множина M елементом самої себе, чи ні? Наприклад, множина всіх множин є множиною і тому належить сама собі, а множина всіх будинків у місті не є будинком, множина студентів в аудиторії не є студентом.

Отже коректно поставити сформульоване питання і щодо множини всіх множин, які не будуть власними елементами. Нехай M - множина всіх тих множин, що не є елементами самих себе. Розглянемо питання: а сама множина M є елементом самої себе чи ні? Якщо припустити, що M Î M, то з означення множини M випливає M Ï M. Якщо ж припустимо, що M Ï M, то з того ж таки означення дістанемо M Î M.

Близьким до парадокса Рассела є так званий "парадокс цирульника": цирульник - це мешканець міста, який голить тих і тільки тих мешканців міста, які не голять самі себе. Проводячи міркування, аналогічні тим, що були зроблені в парадоксі Рассела, дійдемо висновку, що цирульник голить себе в тому і тільки в тому випадку, коли цирульник не голить сам себе.

Багато хто з математиків на початку ХХ ст. не надавали цим парадоксам особливого значення, оскільки в той час теорія множин була відносно новою галуззю математики і не зачіпала інтересів більшості математиків. Однак їхні більш відповідальні та проникливі колеги зрозуміли, що виявлені парадокси стосуються не тільки теорії множин і побудованих на ній розділів класичної математики, але мають безпосереднс відношення до логіки взагалі, тобто до головного інструменту математики.

Зокрема, парадокс Рассела може бути переформульований в термінах логіки і таким чином доданий до відомих з давніх часів логічних парадоксів (парадоксу брехуна, парадоксу всемогутньої істоти тощо).

Якщо проаналізувати всі парадокси теорії множин, то можна зробити висновок, що всі вони обумовлені необмеженим застосуванням так званого принципу абстракції (або принципу згортання), згідно з яким для будь-якої властивості P (x) існує відповідна множина елементів x, які мають властивість P (x). Якщо відкинути це припущення, то всі відомі парадокси теорії множин стають неможливими.

В усіх існуючих аксіоматичних теоріях множин неможливість антиномій ґрунтується на обмеженнях принципу згортання.

Відображення

Визначення і приклади

Нехай задано дві множини Х і Y. Відображення f з множини Х в множину Y кожному елементу х з множини Х ставить у відповідність деякий (один) елемент f (х) з множини Y. Елемент f (х) називають образом елемента х при відображенні f. Символічно відображення записується так: f: Х ® Y чи X Y. У випадку Y = Х кажуть ще про відображення f множини Х в (на) себе.

Якщо Х = { x ₁, x ₂, …, x_n } – скінченна множина, тo відображення f: Х ® Y, можна задати записом з двох рядків f = , де f (х_i) Î Y, i = 1, 2, …, n.

Наприклад, f: Х → Y, Х = {l, 2, 3, 4, 5}, Y = { а, b, c }, f = .

Відображення часто ілюструють за допомогою діаграм (рис. 8), де відповідність між елементами показують стрілками. Відображення задане в попередньому прикладі зображене на рис. 8а. Відповідності рис. 8б та рис. 8в відображеннями не будуть, оскільки на рис. 8б елемент 1 Î X не має образу в множині Y, а на рис. 8в елементу 3 Î X ставиться у відповідність два елементи з множини Y: b та c.

Рис. 8

Приклади відображень:

1) f (x) = є відображенням множини відмінних від нуля елементів множини дійсних чисел R\ {0} в R.

2) Якщо, Х - множина дійсних функцій φ (х), визначених та інтегрованих на інтервалі [ a, b ], то інтеграл є відображенням з множини Х в множину дійсних чисел R.

3) Якщо X - множина кривих скінченної довжини на площині, то можна визначити відображення з Х в множину R ₊ додатних дійсних чисел, яке кожній кривій ставить у відповідність її довжину.

Деякі часткові випадки

1. Відображення f множини Х в множину Х, визначене рівністю f (х) = х, називається тотожним.

2. Якщо Х є підмножиною Y, то відображення Х в Y, визначене рівністю f (х) = х, називається канонічною ін’єкцією Х в Y.

3. Відображення з прямого добутку множин Х ´ Y в X, що ставить у відповідність кожній парі (x, y) Î Х ´ Y елемент х Î Х, називається проекцією на множину X. Аналогічно визначається проекція на множину Y.