1. Довести тотожність для множин: A \ (B Ç C) = (A \ B) È (A \ C)
Розв’язування: Запишемо ланцюжок рівносильних тверджень
x Î A \ (B Ç C) Û (x Î A)i (x Ï B Ç C) Û (x Î A)i (x Î  ) Û (x Î A)i (x Î
) Û (x Î A)i (x Î 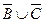 ) Û
) Û
(x Î A)i (x Î  або x Î
або x Î  ) Û (x Î A i x Î
) Û (x Î A i x Î  ) або (x Î A i x Î
) або (x Î A i x Î  ) Û (x Î A i x Ï B) або (x Î A i x Ï С) Û x Î(A \ B) È (A \ C)
) Û (x Î A i x Ï B) або (x Î A i x Ï С) Û x Î(A \ B) È (A \ C)
Таким чином, множини A \ (B Ç C) та (A \ B) È (A \ C) співпадають. Тотожність доведено.
2. Дослідити властивості (ін’єктивність, сюр’єктивність та бієктивніть) відображення f: X → Y, де X – множина прямокутників на площині, Y = R + - множина додатніх дійсних чисел, f (x) = площа (x).
Розв’язування: Введемо такі позначення. Довільний прямокутник x можна подати як впорядковану пару довжин його сторін (ax, bx) де ax та bx – додатні дійсні числа, тоді відображення f (x) = площа (x) визначатиметься виразом f (x) = sx = ax × bx.
a) ін’єктивність. Візьмемо довільне s Î Y та виберемо прямокутник зі сторонами ax і bx =  . Тоді для довільного ax, площа f (x) =
. Тоді для довільного ax, площа f (x) =  = s. Отже, довільне число прямокутників будуть переходити при даному відображенні в одне і те ж число s. Тому відображення не є ін’єктивним;
= s. Отже, довільне число прямокутників будуть переходити при даному відображенні в одне і те ж число s. Тому відображення не є ін’єктивним;
б) сюр’єктивність. Подібно до наведених вище міркувань візьмемо довільне y Î Y та зафіксуємо одну із сторін прямокутника ax = 1. Тоді bx = y і для кожного додатнього цілого числа y Î Y у множині X знайдеться прямокутник зі сторонами (1, y). Значить, відображення сюр’єктивне;
б) бієктивність. Оскільки задане відображення не ін’єктивне, то за означенням воно не є бієктивним.
3. Задано відношення R Í X ´ X, X = N, (x, y) Î R, якщо x 2 – y 2 ділиться на 2 (мається на увазі без остачі). Дослідити відношення на рефлективність, антирефлективність, симетричність, антисиметричність, транзитивність.
Розв’язування: Очевидно, що відношення є рефлективним, бо для довільного x з множини натуральних чисел вираз x 2 ‑ x 2 рівний нулю, а отже ділиться на 2.
Відношення не є рефлективним, бо скажімо для x =7 пара (7,7) належить до відношення.
При аналізі на симетричність припустимо, що (x, y) Î R, і нехай (x 2 – y 2) / 2 = z. Тоді для (y, x), (y 2 – x 2) / 2 = - z, отже і (y, x) Î R. Звідси робимо висновок, що відношення R є симетричним.
Дане відношення не є антисиметричним: для різних елементів x =11 та y =3 з множини натуральних чисел одночасно виконуються умови: x 2 – y 2 ділиться на 2 та y 2 – x 2 ділиться на 2.
З умови належності пари (x, y) відношенню R випливає, що x та y повинні одночасно бути або парними або непарними числами. Для того, щоб (y, z) Î R, необхідно, щоб число z також було або парним або непарним одночасно з числом y, а, отже, і з числом x. Тому умова транзитивності (x R y і y R z Þ x R z) виконується.
Так як, досліджене відношення R є рефлективним, симетричним та транзитивним, то це - відношення еквівалентності.






